Ситуационная (практическая) задача № 2

Ситуационная (практическая) задача № 1

 

При проверке длины 25 деталей, изготовленных станком-автоматом, были обнаружены следующие отклонения от номинала:

–0,307; 0,262; –0,372; 0,765; –0,140; –0,371; –0,113; –0,693; –0,550; –0,694; 0,545; 0,509; –0,150; –0,150; –0,559; –0,065; –0,112; 0,077; 0,698; –0,119; 0,861; 0,386; –0,827; 0,908; –0,047.

Необходимо:

§ Определить исследуемый признак и его тип (дискретный или непрерывный).

§ В зависимости от типа признака построить полигон или гистограмму относительных частот.

§ На основе визуального анализа полигона (гистограммы) сформулировать гипотезу о законе распределения признака.

§ Вычислить выборочные характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое (стандартное) отклонение.

§ Используя критерий согласия «хи-квадрат» Пирсона, проверить соответствие выборочных данных выдвинутому в п.3 закону распределения при уровне значимости 0,05.

§ Для генеральной средней и дисперсии построить доверительные интервалы, соответствующие доверительной вероятности 0,95.

§ С надежностью 0,95 проверить гипотезу о равенстве:

а) генеральной средней значению 1;

б) генеральной дисперсии значению 0,25.

Решение:

1. Тип признака непрерывный, т.к. исходные цифры могут принимать любые дробные значения на определенном промежутке.

Разобьем данные на 5 равных интервалов:

Длина интервала

Интервал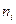

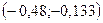
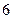
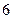
Гистограмма относительных частот

3. На основе анализа гистограммы распределения выдвигаем гипотезу о равномерное законе распределения исследуемого признака.

4. Среднее значение:

Дисперсия:

Среднее квадратическое (стандартное) отклонение:

5. Вводим гипотезы:

Исследуемый признак имеет равномерное распределение:

Исследуемый признак имеет другое распределение:

Условие принятия гипотезы

Вероятность попадания в интервалы:

Интервал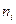
		0,2
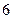
		0,2		0,2
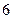
		0,2		0,2
		0,2		0,2
		0,2		0,2
Сумма				0,8

, следует гипотезу о равномерном распределении исследуемого признака принимаем.

6. Доверительный интервал для генерального среднего, при доверительной вероятности 95%:

С вероятностью 95% генеральное среднее находится в интервале от до .

Доверительный интервал для генеральной дисперсии, при доверительной вероятности 95%:

С вероятностью 95% генеральная дисперсия находится в интервале от до .

7а. Вводим гипотезы:

Условие принятия гипотезы

Условие принятия гипотезы выполняется , следует с вероятностью 95% генеральное среднее нельзя считать равным 1.

7б. Вводим гипотезы:

Условие принятия гипотезы

Условие принятия гипотезы выполняется , следует с вероятностью 95% генеральную дисперсию можно считать равной 0,25.

Ситуационная (практическая) задача № 2

В цехе с 10 станками ежедневно регистрировалось число вышедших из строя станков. Всего было проведено 200 наблюдений, результаты которых приведены ниже

Число выбывших станков
Число зарегистрированных случаев

Необходимо:

· Определить исследуемый признак и его тип (дискретный или непрерывный).

· В зависимости от типа признака построить полигон или гистограмму относительных частот.

· На основе визуального анализа полигона (гистограммы) сформулировать гипотезу о законе распределения признака.

· Вычислить выборочные характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое (стандартное) отклонение.

· Для генеральной средней и дисперсии построить доверительные интервалы, соответствующие доверительной вероятности 0,99.

· При уровне значимости 0,05 проверить гипотезу о том, что число выбывших из строя станков имеет распределение Пуассона

Решение:

1. Тип признака дискретный, т.к. исходные цифры могут принимать только целые значения.

Интервал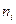
		0,2
		0,315
		0,22
		0,115
		0,085
		0,035
		0,02
7-10		0,01

 

Полигон относительных частот

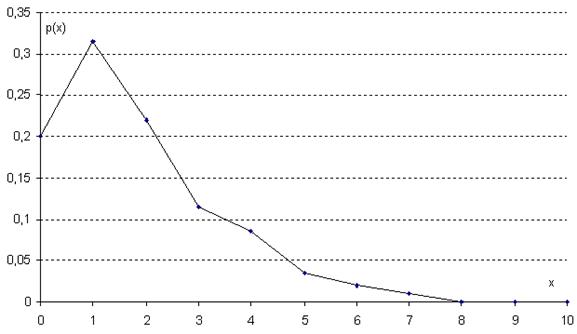
3. На основе анализа полигона относительных частот выдвигаем гипотезу о распределение Пуассона исследуемого признака.

4. Среднее значение:

Дисперсия:

Среднее квадратическое (стандартное) отклонение:

5. Доверительный интервал для генерального среднего, при доверительной вероятности 95%:

С вероятностью 99% генеральное среднее находится в интервале от до .

Доверительный интервал для генеральной дисперсии, при доверительной вероятности 99%:

С вероятностью 99% генеральная дисперсия находится в интервале от до .

6. Вводим гипотезы:

Исследуемый признак имеет распределение Пуассона:

Исследуемый признак имеет другое распределение:

Условие принятия гипотезы

Вероятность попадания в интервалы:

Интервал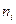
		0,1645	32,89	1,53
		0,2969	59,38	0,22
		0,2679	53,59	1,71
		0,1612	32,24	2,65
		0,0727	14,55	0,41
		0,0263	5,25	0,58
		0,0079	1,58	3,71
7-10		0,0026	0,52	4,19
Сумма				15,01

, следует гипотезу о распределении Пуассона исследуемого признака отвергаем.

Тестовые задания

Необходимо из предложенных вариантов ответа на вопрос теста выбрать единственно верный, по Вашему мнению.

1. Из генеральной совокупности извлечена выборка

xi
ni

Найти относительную частоту варианты

А. 7,5 В. 0,75

Б. 6 Г. 0,075

 

2. Дана выборка 6, 2, 1, 7, 6, 7, 8, 5, 2, 6. Найти несмещенную оценку математического ожидания.

А. 40 В. 5

Б. 4 Г. 2

 

3. Мода вариационного ряда 1, 2, 2, 3, 3, 3, 3, 5, 6, 8 равна

А. 2 В. 8

Б. 3 Г. 2,6

 

4. Дана выборка 3, 2, 3, 5, 6, 2, 5, 8, 4, 2. Найти выборочную дисперсию

А. 3,6 В. 4

Б. 5,4 Г. 5

 

5. Дана выборка 2, 5, 3, 3, 6, 4, 6, 5, 3, 3. Найти несмещенную оценку дисперсии

А. 4 В. 1,8

Б. 5 Г. 2

 

 

6. Дан доверительный интервал (17,5; 18,9) для оценки математического ожидания нормального распределенного количественного признака. Тогда точечная оценка математического ожидания равна

А. 17,5 В. 0,7

Б. 18,2 Г. 18,9

 

7. Дан доверительный интервал (16,4; 17,5) для оценки математического ожидания нормального распределенного количественного признака. Тогда точность оценки равна

А. 16,95 В. 0,45

Б. 0,55 Г. 0,05

 

8. Чему равен квантиль распределения «хи-квадрат» X²_22,0,8?

А. 20,951 В. 27,301

Б. –27,301 Г. 18,114

 

9. Чему равен квантиль распределения Стьюдента t_14,0,9?

А. 1,3450 В. –0,3450

Б. 0,3450 Г. –1,3450

 

10. Соотношением вида P (K < 1,23)= 0,025 можно определить