МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»
Утверждено
на заседании кафедры физики
«20 » мая 2011 г.
Методические указания
к лабораторной работе № 12
«ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ ФИЗИЧЕСКОГО МАЯТНИКА»
Методические указания для бакалавриата
всех профилей по направлениям подготовки:
270800 «Строительство»
270200 «Реконструкция и реставрация архитектурного наследия»
280700 «Техносферная безопасность»
190700 «Технология транспортных процессов»
190600 «Эксплуатация транспортно-технологических машин и комплексов»
230400 «Информационные системы и технологии»
230700 «Прикладная информатика»
120700 «Землеустройство и кадастр»
261400 «Технология художественной обработки материалов»
221700 «Стандартизация и метрология»
100800 «Товароведение»
Ростов-на-Дону
УДК 531.383
Методические указания к лабораторной работе № 12 «Изучение затухающих колебаний физического маятника». – Ростов н/Д: Рост. гос. строит. ун-т, 2011. – 9 с.
Методические указания содержат краткую теорию метода, порядок выполнения лабораторной работы, требования техники безопасности, требования к оформлению результатов, а также перечень контрольных вопросов и тестов.
Предназначены для выполнения лабораторной работы по программе курса физики для студентов бакалавриата очной и заочной форм обучения всех профилей по направлениям:
270800 «Строительство»
270200 «Реконструкция и реставрация архитектурного наследия»
280700 «Техносферная безопасность»
190700 «Технология транспортных процессов»
190600 «Эксплуатация транспортно-технологических машин и комплексов»
230400 «Информационные системы и технологии»
230700 «Прикладная информатика»
120700 «Землеустройство и кадастр»
261400 «Технология художественной обработки материалов»
221700 «Стандартизация и метрология»
100800 «Товароведение»
УДК 531.383
Составители: проф. Н.Н.Харабаев
проф. А.Н.Павлов
Рецензенты: доц. Ю.И.Гольцов
доц. И.Н.Мощенко
Редактор К.Е.Гладких
Темплан 2011, поз.
Подписано в печать
Формат 60х84 1/16. Бумага писчая. Ризограф. Уч.-изд.л. 0,5.
Тираж 100 экз. Заказ
Редакционно-издательский центр
Ростовского государственного строительного университета
334022, Ростов-на-Дону, ул. Социалистическая, 162.
© Ростовский государственный
строительный университет, 2011
Лабораторная работа №12
ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
ФИЗИЧЕСКОГО МАЯТНИКА
Цель работы: ознакомление с основными закономерностями затухающих колебаний на примере колебаний физического маятника.
Приборы и принадлежности: физический маятник, шкала для определения амплитуды колебаний маятника.
Краткая теория эксперимента
Физический маятник – это твердое тело, ось вращения которого не проходит через центр масс. Физический маятник совершает свободные незатухающие гармонические колебания под действием тангенциальной составляющей силы тяжести Ft (Ft = mg sina (рис. 1), где a – угол отклонения физического маятника от положения равновесия).
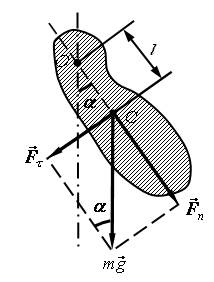
Рис. 1
Если физический маятник массой m отклонен от положения равновесия на некоторый угол a, то момент M возвращающей силы Ft:
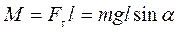, где
l – плечо силы Ft, то естьрасстояние от центра масс (точка С) до оси маятника (рис. 1).
В случае малых колебаний физического маятника,то есть для малых углов отклонения маятника от положения равновесия sin a » a и тогда
.
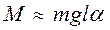Согласно основному закону динамики вращательного движения:
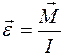или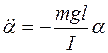 
,
где I — момент инерции маятника относительно его оси вращения.
Знак минус в последнем уравнении обусловлен тем, что вектора момента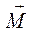 
возвращающей силы 
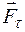и угла поворота 
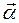имеют противоположные направления.
Обозначив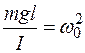 
, получим дифференциальное уравнение свободных незатухающих гармонических колебаний физического маятника:
.
Решением этого дифференциального уравнения является функция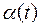 
:
,
где 
– угол отклонения физического маятника от положения равновесия в момент времени t;
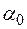– амплитудаколебаний, то есть наибольший угол отклонения физического маятника от положения равновесия;
w 0 – круговая (циклическая) частота;
(w 0 t + j0) – фаза колебания в момент времени t;
j 0 – начальная фаза колебаний.
В данной лабораторной работе используется физический маятник в виде металлического стержня, на свободном конце которого расположен диск (рис. 2), обеспечивающий затухания колебаний маятника за счет силы сопротивления воздуха.
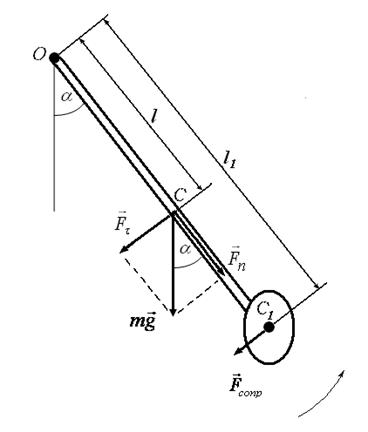
Рис. 2
Для малых колебаний маятника сила сопротивления Fcопр со стороны воздуха будет пропорциональна скорости движения маятника: Fcопр=−r·υ, где r – коэффициент сопротивления, а знак минус указывает на противоположные направления векторов силы сопротивления и скорости.
Учитывая, что диаметр диска значительно меньше длины стержня в используемом физическом маятнике, за точку приложения силы Fcопр можно принять центр диска при определении момента этой силы:
Mcопр = Fcопр · l 1= rυl 1.
Так как υ=ωl1 (ω – угловая скорость), то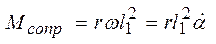 
.
С учетом силы 
и силы сопротивления уравнение динамики вращательного движения примет вид:
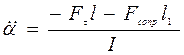, откуда 
.
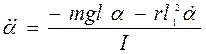Обозначив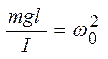 
и 
, получим дифференциальное уравнение свободных затухающих колебаний физического маятника:
.
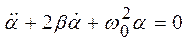Решением этого дифференциального уравнения является функция α(t):
,
где 
– амплитуда свободных затухающих гармонических колебаний физического маятника в момент времени t;
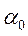– начальная амплитуда, т.е. амплитуда колебаний в момент времени t = 0,
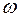– круговая (циклическая) частота: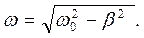 
График функции α(t), описывающей затухающие колебания физического маятника, приведен на рис. 3.
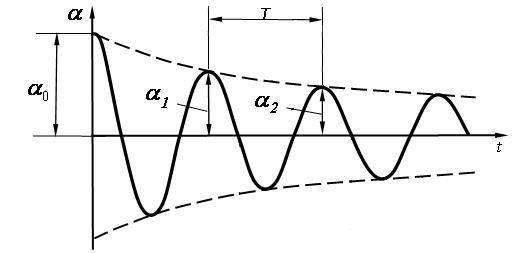
Рис. 3
Амплитуда свободных затухающих гармонических колебаний физического маятника со временем уменьшается в соответствии с уравнением:
, где
n – номер в последовательности затухающих колебаний (рис. 3),
Т – условный период колебаний.
Отношение амплитуд двух последовательных колебаний αn/αn+1 (рис. 3), соответствующих моментам времени, отличающихся на период Т, называется декрементом затухания D:
.
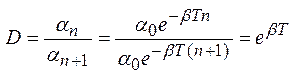Ряд убывающих амплитуд αn затухающих колебаний может быть записан в виде убывающей геометрической прогрессии, то есть:
.
Логарифм декремента затухания называется логарифмическим декрементом затухания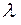 
: 
.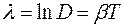