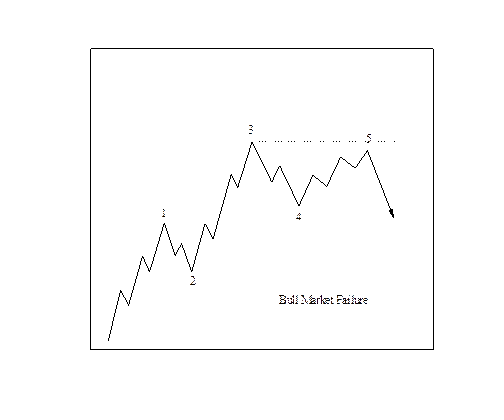До сих пор мы говорили, в основном, об импульсных волнах, которые совпадают с направлением основной тенденции. Теперь мы переходим к корректирующим волнам. Как правило, волны этого типа менее четко определены, и поэтому их выявление и анализ затруднен. Впрочем, им присуща одна характерная черта: корректирующие волны никогда не подразделяются на пять волн. За исключением треугольников, типичная корректирующая волна состоит из трех волн. Корректирующие волны образуют четыре модели: зигзаги (zig-zags), плоские волны (flats), треугольники, двойные и тройные тройки (double and triple threes).
Рис. П2.7 Модель "неудача" на бычьем рынке.
Зигзаги
"Зигзагом" называют трехволновую корректирующую конфигурацию, направленную против хода основной тенденции. Эта модель разбивается в последовательность: 5-3-5. На рис. П2.9 и П2.10 показаны примеры корректирующих зигзагов для бычьего рынка. Обратите внимание, что средняя волна В не достигает начальной точки волны А. Волна С, в свою очередь, значительно перекрывает уровень, на котором заканчивается волна А.
Рис. П2.8 Модель "неудача" на медвежьем рынке.
| Рис. П2.9 Зигзаг бычьего рынка | Рис. П2.10 Зигзаг медвежьего рынка (5-3-5). |
Менее распространенный вариант модели зигзаг известен под названием "двойной зигзаг". Пример такой модели мы видим на рис. П2.11. Эта конфигурация иногда встречается как часть больших корректирующих моделей. Фактически здесь мы имеем дело с двумя различными зигзагами 5-3-5, соединенными включенной в них конфигурацией a-b-c.
Плоские волны
Плоская коррекция, в отличие от зигзагообразной, образует конфигурацию 3-3-5. Обратите внимание, что на примерах волна А состоит из трех волн, а не из пяти. В целом плоская волна является скорее кон фигурацией консолидации, чем коррекции. Она свидетельствует о силе бычьего рынка. На рис. П2.12, П2.13 показаны примеры плоских классических волн.
|
|
Так, на бычьем рынке в ходе оживления волна В достигает вершины волны А, демонстрируя более высокий рыночный потенциал. Завершающая волна С заканчивает свой ход у основания волны А или чуть ниже - в отличие от модели зигзаг, которая опускается гораздо ниже.
Рис. П2.11 Двойной зигзаг.
Встречаются два исключения плоской классической конфигурации коррекции. Первый тип такого исключения показан на рис. П2.14 и П2.15. Обратите внимание, что на бычьем рынке вершина волны В превосходит вершину волны А, а волна С, в свою очередь, опускается ниже основания волны А.
| Рис. П2.12 Нормальная плоская коррекция бычьего рынка. | Рис. П2.13 Нормальная плоская коррекция бычьего рынка (3-3-5) |
| Рис. П2.14"Неправильная" плоская коррекция бычьего рынка. | Рис. П2.15 "Неправильная" плоская коррекция бычьего рынка (3-3-5) |
Второе исключение происходит, когда волна В достигает вершины волны А, в то время как волна С так и не опускается до уровня основания волны А. Естественно, в этом случае бычий рынок обладает более высоким рыночным потенциалом. Примеры такого отклонения от правил для бычьего рынков показаны на рис. П2.16 и П2.17.
| Рис. П2.16Перевернутая "неправильная" плоская коррекция бычьего рынка | Рис. П2.17Перевернутая "неправильная" плоская коррекция бычьего рынка (3-3-5) |
|
|
Рис. П2.18. Плоская "бегущая" коррекция (3-3-5).
Последний вариант плоской коррекции свидетельствует о наличии еще большего рыночного потенциала. Он называется "бегущей" (running) коррекцией.
Пример "бегущей" коррекции бычьего рынка показан на рис. П2.18.
Обратите внимание, что волна b поднимается гораздо выше вершины волны а, а волна с остается выше вершины волны 1, которая, напомним, является импульсной. Данная корректирующая конфигурация встречается довольно редко, она характерна для рынка, потенциал которого настолько значителен, что коррекции так и не удается полностью сформироваться.
Треугольники
Треугольники обычно появляются на четвертой волне, предшествуя последнему движению в направлении основной тенденции (они также могут появиться на волне b, входящей в корректирующую конфигурацию а-b-с). Таким образом, при восходящей тенденции треугольники можно охарактеризовать как бычью и медвежью модель одновременно. Мы называем ее бычьей потому, что треугольники показывают возобновление тенденции роста. А медвежьи они потому, что сигнализируют также о приближении цен к вершине, что, как правило, происходит после еще одной волны роста.
Принципы интерпретации треугольников по Эллиоту почти не отличаются от классического анализа этих моделей. Однако теория волн позволяет делать это более точно. Треугольник обычно является моделью продолжения тенденции - именно так его описывает и Эллиот. Треугольник подразделяется на пять волн, причем каждая из них в свою очередь складывается из трех волн. Эллиот также выделяет четыре различных типа треугольников - восходящий, нисходящий, симметричный и расширяющийся. На рис. П2.19 вы видите примеры всех четырех разновидностей модели для тенденций роста и падения.
|
|
A. Восходящий (верхняя линия горизонтальная, нижняя – поднимающаяся).
B. Нисходящий (верхняя линия опускающая, нижняя – горизонтальная).
C. Симметричный (верхняя линия опускающая, нижняя – поднимающаяся).
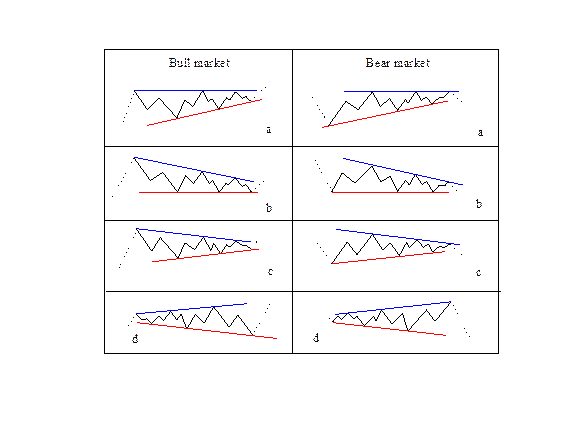D. Расширяющийся (верхняя линия поднимающаяся, нижняя – опускающая).
Рис. П2.19. Треугольники корректирующих волн (горизонтальные).
Двойные и тройные тройки
Последней разновидностью корректирующих волн является сравнительно редко встречающаяся на графиках сложная конфигурация, состоящая из двух или трех простых моделей (рис. П2.20, П2.21). На первом примере (рис. П2.20) мы видим семь волн, представляющих собой комбинацию двух конфигураций типа а-b-с. На рис. П2.21 три конфигурации а-b-с, соединяясь, образуют одиннадцать волн.
Рис. П2.20. Двойная тройка.
На этом мы заканчиваем обзор основных моделей теории волн Эллиота. Далее мы должны коснуться двух важных особенностей волнового анализа - во-первых, так называемого "правила чередования" и, во-вторых, закономерностей построения ценового канала.