Графоаналитическое решение основной задачи линейного программирования (ОЗЛП).
Постановка ОЗЛП:
Вариант 8.






Ограничения:




 ,
, 
Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом) (рисунок 1).

Рисунок 1. Полуплоскости, заданные неравенствами ограничений.
Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.
Обозначим границы области многоугольника решений (рисунок 2).

Рисунок 2. Область допустимых решений ОЗЛП.
Рассмотрим целевую функцию задачи  .
.
Построим прямую, отвечающую значению функции. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации. Начало вектора – точка (0; 0), конец – точка (0.5; 3). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике (рисунок 3) эта прямая обозначена пунктирной линией.

Рисунок 3. Графическое решение ОЗЛП.
Прямая φ(x) = const пересекает область в точке F. Так как точка F получена в результате пересечения прямых (1) и (2), то ее координаты удовлетворяют уравнениям этих прямых:

Решив систему уравнений, получим: x1 = 4, x2 = 2.
Откуда найдем максимальное значение целевой функции:
φ = 0.5*4 + 3*2 = 8.
Задание 2б.
Вариант 8.

Ограничения:
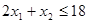


 ,
,  .
.
Необходимо найти минимальное значение целевой функции F = x1+2x2 → min,при системе ограничений:
2x1+x2≤18,
x1-2x2≤10,
x1+2x2≥14,
x1 ≥0
x2 ≥0
Введем
2x1 +1x2 +1x3 +0x4 +0x5 +0x6 =18
1x1-2x2 +0x3 +1x4 +0x5 +0x6 =10
1x1 +2x2 +0x3 +0x4-1x5 +1x6 =14
2y1+y2+y3≤1
y1-2y2+2y3≤2
18y1+10y2+14y3 → max
y1 ≤ 0
y2 ≤ 0
y3 ≥ 0
| Исходная задача I | Двойственная задача II | |
| x1 ≥ 0 | ↔ | 2y1+y2+y3≤1 |
| x2 ≥ 0 | ↔ | y1-2y2+2y3≤2 |
| x1+2x2 → min | ↔ | 18y1+10y2+14y3 → max |
| 2x1+x2≤18 | ↔ | y1 ≤ 0 |
| x1-2x2≤10 | ↔ | y2 ≤ 0 |
| x1+2x2≥14 | ↔ | y3 ≥ 0 |
Переменные yj называются допустимым решением двойственной задачи. Переменные yj называются оптимальными, если они допустимые и на них целевая функция достигает максимальное значения.
Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи.
Оптимальный план двойственной задачи равен:
y1 = 0, y2 = 0, y3 = 1
Z(Y) = 18*0+10*0+14*1 = 14
Шаг №1. Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).
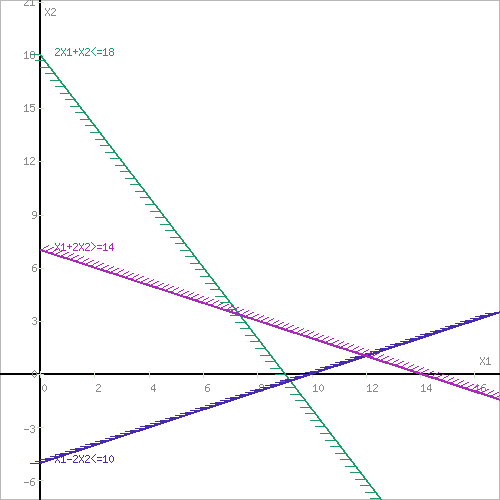
Шаг №2. Границы области допустимых решений.
Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.
Обозначим границы области многоугольника решений.

Шаг №3. Рассмотрим целевую функцию задачи F = x1+2x2 → min.
Построим прямую, отвечающую значению функции F = 0: F = x1+2x2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (1; 2). Будем двигать эту прямую параллельным образом. Поскольку нас интересует минимальное решение, поэтому двигаем прямую до первого касания обозначенной области. На графике эта прямая обозначена пунктирной линией.

Прямая F(x) = const пересекает область в точке C. Так как точка C получена в результате пересечения прямых (1) и (3), то ее координаты удовлетворяют уравнениям этих прямых:
2x1+x2=18
x1+2x2=14
Решив систему уравнений, получим: x1 = 7.3333, x2 = 3.3333
Откуда найдем минимальное значение целевой функции:
F(X) = 1*7.3333 + 2*3.3333 = 14
Поскольку функция цели F(x) параллельна прямой (3), то на отрезке CA функция F(x) будет принимает одно и тоже минимальное значение.
Для определения координат точки A решим систему двух линейных уравнений:
x1+2x2=14
x1=0
Решив систему уравнений, получим: x1 = 0, x2 = 7
Откуда найдем минимальное значение целевой функции:
F(X) = 1*0 + 2*7 = 14
Решение задачи 2 на Matlab.
>> A=[1,-1.5;-0.5,2;1,-2;-2,2];
>> b=[1;2;0.5;1];
>> c=[0.5,3];
>> [x,fval]=linprog(c,A,b)
Optimization terminated successfully.
x =
-1.5000
-1.0000
fval =
-3.7500