Физика, часть II
Задание{{ 9-1 }}
Если в колебательном контуре заряд на обкладках конденсатора изменяется по закону:
q=13,5 e–2 t cos(340 t + π/4) (Кл), то добротность контура равна:
−: 30
−: 16
−: 11
−: 85
−: 44
@
Задание{{ 9-2 }}
Если в колебательном контуре заряд на обкладках конденсатора изменяется по закону:
q=13,5 e–4 t cos(325 t + π/4) (Кл), то добротность контура равна:
−: 30
−: 16
−: 11
−: 85
−: 41
@
Задание{{ 9-3 }}
Если в колебательном контуре заряд на обкладках конденсатора изменяется по закону:
q=13,5 e–5 t cos(300 t + π/4) (Кл), то добротность контура равна:
−: 30
−: 16
−: 11
−: 85
−: 44
@
Задание{{ 9-4 }}
Если в колебательном контуре заряд на обкладках конденсатора изменяется по закону:
q=13,5 e–10 t cos(320 t + π/4) (Кл), то добротность контура равна:
−: 30
−: 16
−: 11
−: 85
−: 44
@
Задание{{ 9-5 }}
Если в колебательном контуре заряд на обкладках конденсатора изменяется по закону:
q=13,5 e–15 t cos(330 t + π/4) (Кл), то добротность контура равна:
−: 30
−: 16
−: 11
−: 85
−: 44
@
Задание{{ 9-6 }}
Если в колебательном контуре L= 2,3 мкГн, С=3,3нФ (см. рис.), ток в цепи изменяется по закону I =0,23 cos(1,15х107 t + π/4) (А), то величина максимального заряда на конденсаторе равна (в нКл):
−: 19,3
−: 20,0
−: 32,7
−: 42,8
−: 53,9
@
Задание{{ 9-7 }}
Если в колебательном контуре L= 2,2 мкГн, С=3,2 нФ (см. рис.), ток в цепи изменяется по закону I =0,23 cos(1,19х107 t + π/4) (А), то величина максимального заряда на конденсаторе равна (в нКл):
−: 19,3
−: 21,7
−: 32,7
−: 42,8
−: 53,9
@
Задание{{ 9-8 }}
Если в колебательном контуре L=2,6мкГн, С=3,7 нФ (см. рис.), ток в цепи изменяется по закону I =0,55 cos(1,02х107 t + π/4) (А), то величина максимального заряда на конденсаторе равна (в нКл):
|
|
−: 19,3
−: 21,7
−: 32,7
−: 42,8
−: 53,9
@
Задание{{ 9-9 }}
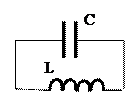Если в колебательном контуре L= 2,5мкГн, С=3,5нФ (см. рис.), ток в цепи изменяется по закону I =0,45cos(1,05х107 t + π/4) (А), то величина максимального заряда на конденсаторе равна (в нКл):
−: 19,3
−: 21,7
−: 32,7
−: 42,8
−: 53,9
@
Задание{{ 9-10 }}
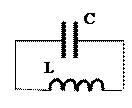Если в колебательном контуре L= 2,4мкГн, С=3,4нФ (см. рис.), ток в цепи изменяется по закону I =0,36 cos(1,1х107 t + π/4) (А), то величина максимального заряда на конденсаторе равна (в нКл):
−: 19,3
−: 21,7
−: 32,7
−: 42,8
−: 53,9
@
Задание{{ 9-11 }}
Если в колебательном контуре с индуктивностью L= 49,69Гн совершаются установившиеся колебания по закону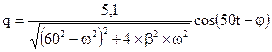 
(Кл), то электроемкость конденсатора в контуре равна (в мкФ):
−: 7,6
−: 5,1
−: 6,7
−: 4,6
−: 5,59
@
Задание{{ 9-12 }}
Если в колебательном контуре с индуктивностью L= 41,46 Гн совершаются установившиеся колебания по закону 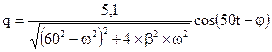(Кл), то электроемкость конденсатора в контуре равна (в мкФ):
−: 7,6
−: 5,1
−: 6,7
−: 4,6
−: 5,95
@
Задание{{ 9-13 }}
Если в колебательном контуре с индуктивностью L= 36,55Гн совершаются установившиеся колебания по закону 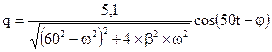(Кл), то электроемкость конденсатора в контуре равна (в мкФ):
−: 7,6
−: 5,1
−: 6,7
−: 4,6
−: 5,95
@
Задание{{ 9-14 }}
Если в колебательном контуре с индуктивностью L= 60,39Гн совершаются установившиеся колебания по закону 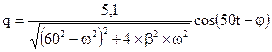(Кл), то электроемкость конденсатора в контуре равна (в мкФ):
−: 7,6
−: 5,1
−: 6,7
−: 4,6
−: 5,95
@
Задание{{ 9-15 }}
Если в колебательном контуре с индуктивностью L= 54,47 Гн совершаются установившиеся колебания по закону 
(Кл), то электроемкость конденсатора в контуре равна (в мкФ):
|
|
−: 7,6
−: 5,1
−: 6,7
−: 4,6
−: 5,95
@
Задание{{ 9-16 }}
Если в колебательном контуре L=3,5 мкГн, С=2 нФ (см. рис.), заряд на конденсаторе изменяется по закону Q =1,85 cos(0,378 t + π/4) Кл, то амплитуда тока в цепи равна (в А):
−: 0,8
−: 0,7
−: 0,6
−: 1,3
−: 1,5
@
Задание{{ 9-17 }}
Если в колебательном контуре L=4 мкГн, С=3нФ (см. рис.), заряд на конденсаторе изменяется по закону Q =2,08 cos(0,289 t + π/4) Кл, то амплитуда тока в цепи равна (в А):
−: 0,8
−: 0,7
−: 0,6
−: 1,3
−: 1,5
@
Задание{{ 9-18 }}
Если в колебательном контуре L=4,5 мкГн, С=4 нФ (см. рис.), заряд на конденсаторе изменяется по закону Q =5,52 cos(0,236 t + π/4) Кл, то амплитуда тока в цепи равна (в А):
−: 0,8
−: 0,7
−: 0,6
−: 1,3
−: 1,5
@
Задание{{ 9-19 }}
Если в колебательном контуре L=2,5 мкГн, С=1 нФ (см. рис.), заряд на конденсаторе изменяется по закону Q =2,37 cos(0,63t + π/4) Кл, то амплитуда тока в цепи равна (в А):
−: 0,8
−: 0,7
−: 0,6
−: 1,3
−: 1,5
@
Задание{{ 9-20 }}
Если в колебательном контуре L=3мкГн, С=5нФ (см. рис.), заряд на конденсаторе изменяется по закону Q =3,1 cos(0,26 t + π/4) Кл, то амплитуда тока в цепи равна (в А):
−: 0,8
−: 0,7
−: 0,6
−: 1,3
−: 1,5
@
Задание{{ 9-21 }}
Если в колебательном контуре с электроемкостью С=111 мкФ совершаются установившиеся колебания по закону 
(Кл), то индуктивность цепи равна (в Гн):
−: 1,3
−: 1,5
−: 1,8
−: 2,1
−: 2,5
@
Задание{{ 9-22 }}
Если в колебательном контуре с электроемкостью С= 185 мкФ совершаются установившиеся колебания по закону (Кл), то индуктивность цепи равна (в Гн):
|
|
−: 1,3
−: 1,5
−: 1,8
−: 2,1
−: 2,5
@
Задание{{ 9-23 }}
Если в колебательном контуре с электроемкостью С= 154 мкФ совершаются установившиеся колебания по закону (Кл), то индуктивность цепи равна (в Гн):
−: 1,3
−: 1,5
−: 1,8
−: 2,1
−: 2,5
@
Задание{{ 9-24 }}
Если в колебательном контуре с электроемкостью С= 214 мкФ совершаются установившиеся колебания по закону 
(Кл), то индуктивность цепи равна (в Гн):
−: 1,3
−: 1,5
−: 1,8
−: 2,1
−: 2,5
@
Задание{{ 9-25 }}
Если в колебательном контуре с электроемкостью С= 132 мкФ совершаются установившиеся колебания по закону (Кл), то индуктивность цепи равна (в Гн):
−: 1,3
−: 1,5
−: 1,8
−: 2,1
−: 2,5
@
Задание{{ 9-26 }}
Если в колебательном контуре заряд на обкладках конденсатора изменяется по закону:
q=13,5 e–1,1·t cos(370t + π/4) (Кл), то логарифмический декремент затухания контура равен:
−: 0,021
−: 0,0034
−: 0,009
−: 0,019
−: 0,025
@
Задание{{ 9-27 }}
Если в колебательном контуре заряд на обкладках конденсатора изменяется по закону:
q=13,5 e–0,3·tcos(200t + π/4) (Кл), то логарифмический декремент затухания контура равен:
−: 0,021
−: 0,0034
−: 0,009
−: 0,019
−: 0,025
@
Задание{{ 9-28 }}
Если в колебательном контуре заряд на обкладках конденсатора изменяется по закону:
q=13,5 e–0,2·t cos(350t + π/4) (Кл), то логарифмический декремент затухания контура равен:
−: 0,021
−: 0,0034
−: 0,009
−: 0,019
−: 0,025
@
Задание{{ 9-29 }}
Если в колебательном контуре заряд на обкладках конденсатора изменяется по закону:
q=13,5 e–1,5·t cos(380 t + π/4) (Кл), то логарифмический декремент затухания контура равен:
−: 0,021
−: 0,0034
−: 0,009
−: 0,019
−: 0,025
@
Задание{{ 9-30 }}
Если в колебательном контуре заряд на обкладках конденсатора изменяется по закону:
q=13,5 e–1·t cos(300 t + π/4) (Кл), то логарифмический декремент затухания контура равен:
−: 0,021
−: 0,0034
−: 0,009
−: 0,019
−: 0,025
@
Задание{{ 9-31 }}
Если при свободных электрических колебаниях сопротивление R=1 Ом, индуктивность
L= 0,5 Гн, то коэффициент затухания равен (в с-1):
−: 35
−: 12,5
−: 5
−: 2,5
−: 1
@
Задание{{ 9-32 }}
Если при свободных электрических колебаниях сопротивление R=2 Ом, индуктивность
L= 0,4 Гн, то коэффициент затухания равен (в с-1):
−: 35
−: 12,5
−: 5
−: 2,5
−: 1
@
Задание{{ 9-33 }}
Если при свободных электрических колебаниях сопротивление R=3Ом, индуктивность
L= 0,3 Гн, то коэффициент затухания равен (в с-1):
−: 35
−: 12,5
−: 5
−: 2,5
−: 1
@
Задание{{ 9-34 }}
Если при свободных электрических колебаниях сопротивление R=7Ом, индуктивность
L= 0,1 Гн, то коэффициент затухания равен (в с-1):
−: 35
−: 12,5
−: 5
−: 2,5
−: 1
@
Задание{{ 9-35 }}
Если при свободных электрических колебаниях сопротивление R=5 Ом, индуктивность
L= 0.2 Гн то коэффициент затухания равен (в с-1):
−: 35
−: 12,5
−: 5
−: 2,5
−: 1
@
Задание{{ 9-36 }}
Если в колебательном контуре с сопротивлением R=3 Ом и индуктивностью L = 0,6Гн циклическая частота свободных затухающих электрических колебаний равна ω= 3рад/с, то добротность контура равна:
−: 0,17
−: 0,2
−: 0,6
−: 0,23
−: 0,625
@
Задание{{ 9-37 }}
Если в колебательном контуре с сопротивлением R= 6 Ом и индуктивностью L = 0,2 Гн циклическая частота свободных затухающих электрических колебаний равна ω= 5рад/с, то добротность контура равна:
−: 0,17
−: 0,2
−: 0,6
−: 0,23
−: 0,625
@
Задание{{ 9-38 }}
Если в колебательном контуре с сопротивлением R=8 Ом и индуктивностью L = 0,4 Гн циклическая частота свободных затухающих электрических колебаний равна ω= 4рад/с, то добротность контура равна:
−: 0,17
−: 0,2
−: 0,6
−: 0,23
−: 0,625
@
Задание{{ 9-39 }}
Если в колебательном контуре с сопротивлением R= 7 Ом и индуктивностью L = 0,8 Гн циклическая частота свободных затухающих электрических колебаний равна ω= 2 рад/с, то добротность контура равна:
−: 0,17
−: 0,2
−: 0,6
−: 0,23
−: 0,625
@
Задание{{ 9-40 }}
Если в колебательном контуре с сопротивлением R= 4 Ом и индуктивностью L = 1 Гн циклическая частота свободных затухающих электрических колебаний равна ω= 2.5 рад/с, то добротность контура равна:
−: 0,17
−: 0,2
−: 0,6
−: 0,23
−: 0,625
@
Задание{{ 9-41 }}
Если в колебательном контуре с сопротивлением R= 4 Ом и индуктивностью L = 1 Гн циклическая частота свободных затухающих электрических колебаний равна ω= 2.5 рад/с, то добротность контура равна:
−: 0,17
−: 0,2
−: 0,6
−: 0,23
−: 0,625
@
Задание{{ 9-42 }}
Если в колебательном контуре заряд на обкладках конденсатора изменяется по закону
q= 2·cos(4,19·t + π/6) (Кл), то период собственных колебаний контура равен (в с):
−: 0,52
−: 30
−: 1,5
−: 0,67
−: 8,4
@
Задание{{ 9-43 }}
Если в колебательном контуре заряд на обкладках конденсатора изменяется по закону
q= 2·cos(4,19·t + π/6) (Кл), то начальная фаза равна (в рад):
−: 0,52
−: 30
−: 1,5
−: 0,67
−: 8,4
@
Задание{{ 9-44 }}
Если в колебательном контуре заряд на обкладках конденсатора изменяется по закону
q= 2·cos(4,19·t + π/6) (Кл), то частота колебаний равна (в Гц):
−: 0,52
−: 30
−: 1,5
−: 0,67
−: 8,4
@
Задание{{ 9-45 }}
Если в колебательном контуре заряд на обкладках конденсатора изменяется по закону
q= 2·cos(4,19· t + π/6) (Кл), то начальная фаза равна (в градусах):
−: 0,52
−: 30
−: 1,5
−: 0,67
−: 8,4
@
Задание{{ 9-46 }}
Если в колебательном контуре заряд на обкладках конденсатора изменяется по закону
q= 2·cos(4,19·t + π/6) (Кл), то максимальное значение тока в цепи равно (в А):
−: 0,52
−: 30
−: 1,5
−: 0,67
−: 8,4
@
Задание{{ 9-47 }}
В колебательном контуре, представленном на рисунке, если L= 8 мГн, C= 2 мкФ, то колебательный процесс перейдет в апериодический при сопротивлении (в Ом):
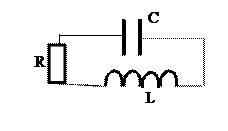−: 100
−: 109,5
−: 89,4
−: 77,5
−: 126,5
@
Задание{{ 9-48 }}
В колебательном контуре, представленном на рисунке, если L=6 мГн, C= 2 мкФ, то колебательный процесс перейдет в апериодический при сопротивлении (в Ом):
−: 100
−: 109,5
−: 89,4
−: 77,5
−: 126,5
@
Задание{{ 9-49 }}
В колебательном контуре, представленном на рисунке, если L= 3 мГн, C= 2 мкФ, то колебательный процесс перейдет в апериодический при сопротивлении (в Ом):
−: 100
−: 109,5
−: 89,4
−: 77,5
−: 126,5
@
Задание{{ 9-50 }}
В колебательном контуре, представленном на рисунке, если L= 5 мГн, C= 2 мкФ, то колебательный процесс перейдет в апериодический при сопротивлении (в Ом):
−: 100
−: 109,5
−: 89,4
−: 77,5
−: 126,5
@
Задание{{ 9-51 }}
В колебательном контуре, представленном на рисунке, если L=4 мГн, C= 2 мкФ, то колебательный процесс перейдет в апериодический при сопротивлении (в Ом):
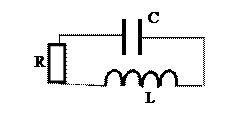−: 100
−: 109,5
−: 89,4
−: 77,5
−: 126,5
@
Задание{{ 9-52 }}
В колебательном контуре, представленном на рисунке, R=1 Ом, L=2 мГн, C=10 мкФ. Период колебаний равен (в мс):
−: 51,1
−: 0,889
−: 6,28
−: 0,949
−: 2,98
@
Задание{{ 9-53 }}
В колебательном контуре, представленном на рисунке, R=10 Ом, L=2 мГн, C=10мкФ. Период колебаний равен (в мс):
−: 51,1
−: 0,889
−: 6,28
−: 0,949
−: 2,98
@
Задание{{ 9-54 }}
В колебательном контуре, представленном на рисунке, R=27 Ом, L=2 мГн, C=10мкФ. Период колебаний равен (в мс):
−: 51,1
−: 0,889
−: 6,28
−: 0,949
−: 2,98
@
Задание{{ 9-55 }}
В колебательном контуре, представленном на рисунке, R=28 Ом, L=2 мГн, C=10мкФ. Период колебаний равен (в мс):
−: 51,1
−: 0,889
−: 6,28
−: 0,949
−: 2,98
@
Задание{{ 9-56 }}
В колебательном контуре, представленном на рисунке, R=28,28 Ом, L=2 мГн, C=10мкФ. Период колебаний равен (в мс):
−: 51,1
−: 0,889
−: 6,28
−: 0,949
−: 2,98
@
Задание{{ 9-57 }}
Если в колебательном контуре с индуктивностью L= 5 Гн совершаются установившиеся колебания по закону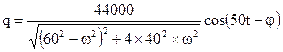 
(Кл), то электроемкость контура равна (в мкФ):
−: 7,96
−: 20
−: 0,4
−: 220
−: 55,5
@
Задание{{ 9-58 }}
Если в колебательном контуре с индуктивностью L= 5 мГн совершаются установившиеся колебания по закону 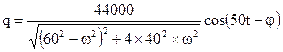(Кл), то активное сопротивление контура равно (в Ом):
−: 7,96
−: 20
−: 0,4
−: 220
−: 55,5
@
Задание{{ 9-59 }}
Если в колебательном контуре с индуктивностью L= 5 Гн совершаются установившиеся колебания по закону 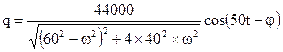(Кл), то электроемкость контура равна (в мкФ):
−: 7,96
−: 20
−: 0,4
−: 220
−: 55,5
@
Задание{{ 9-60 }}
Если в колебательном контуре с индуктивностью L= 5 мГн совершаются установившиеся колебания по закону 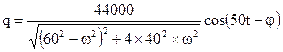(Кл), то частота колебаний контура равна (в Гц):
−: 7,96
−: 20
−: 0,4
−: 220
−: 55,5
@
Задание{{ 9-61 }}
Если в колебательном контуре с индуктивностью L= 5 мГн совершаются установившиеся колебания по закону 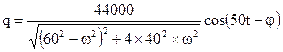(Кл), то резонансная частота равна (в рад/с):
−: 7,96
−: 20
−: 0,4
−: 220
−: 55,5
@