Часть 1. Вступление
Над вопросом «что такое жизнь» люди размышляют веками, наверное, с того самого момента, как люди лишь появились. Вопросы «откуда мы» и «для чего мы тут» крутятся в голове с того самого момента, как только любой из нас начинает осмысленно размышлять.
Сама философия зародилась для решения этого нерешаемого вопроса.
В том, что такое жизнь, как она появилась, как проходит и т.д., мы с вами и попробуем разобраться в данном ЭССЕ.
Часть 2. Мое понимание
На разных этапах моей жизни я имела разные представления и понимания концепции мироздания и истоков всего. На данной ступени моего развития, на которой я стою сейчас, мне удалось разработать более-менее подробную схему представления устройства мира и жизни в нем. Понимания того, как зарождается жизнь, по каким принципам она в нем находится, и чем таким эта «жизнь» является.
Своим следующим описанием этого понимания я откровенно предоставляю вашей оценке свои размышления, длиною в мою 20,5-летнюю жизнь.
Так же я всегда открыта к обсуждению и уточнению этой и иных теорий существования всего.
А теперь меньше слов, больше дела. Приступим.
Глава 1. Как формируется жизнь?
Что же такое «жизнь» в моем понимании?
Жизнь – это абстрактная сущность, имеющаяся в мире вне простора нашего понимания, обладающая некоторыми компонентами (Рисунок 1):
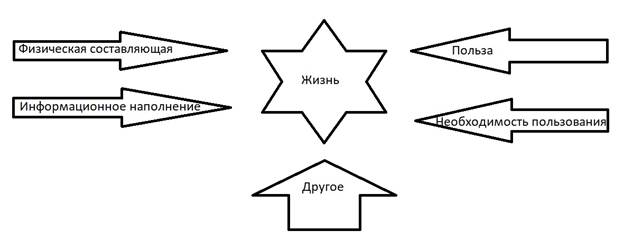
Рисунок 1
Ø Физическая составляющая – это материальная оболочка любой сущности, обладающей собственной жизнью;
Ø Информационное наполнение – это доля информации, которую несет в себе сущность для восприятия иными сущностями;
Ø Польза – какой-то коэффициент полезности, что несет в себе сущность;
Ø Необходимость пользования – необходимость к воздействию с этой сущностью иными сущностями;
Ø Другое – иные факторы, которые на текущий момент мне не удалось описать.
Данная схема описывает принцип создания, сохранения и поддержания жизни, как непрекращающегося процесса, постоянного и цикличного. В следующей главе мы разберем подробнее это понятие.
Глава 2. Как жизнь существует?
Свою концепцию я условно назвала «теория пустого множества» или другое ее название «теория зеркала». У нее есть множество пунктов и подпунктов, уточняющий предыдущие понятия и углубляющиеся в них.
Самым первым и самым главным принципом является следующее:
v «Существуем не «мы», как конкретное значение, а «мы», как пустое, обладающее свойством заполняться, множество».
Объясню на примере, близком мне по духу. Компьютер и двоичная система счисления. 0 – значит информации нет, 1 – информация есть. В этой позиционной системе счисления очень простая логика. Существует пустая ячейка, имеющая свойство заполняемости (т.е. вариант быть 0 или 1) и эта ячейка, при определенном намерении, как раз становится заполненной, либо продолжает быть пустой.
Отсюда сразу появляется вопрос, можно ли измерить это множество?
В моем понимании так же прописан следующий принцип:
v «Мы» неизмеримо, т.е. не обладает конкретной единицей.
И если та же двоичная система счисления способна быть описанной, то в моем понимании понятие несет условный, неописуемый характер.
Вот тут мы и приближаемся к тому, что же такое «принцип зеркала».
Помочь описать сам принцип нам может следующая схема:
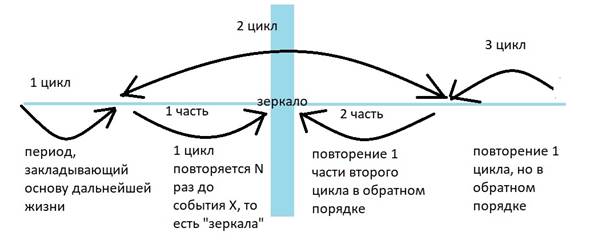
Рисунок 2
Из нее мы видим следующее:
· Понятие «жизнь» несет в себе 3 цикла, у каждого из которых имеется определенное описание
· 1 цикл характеризуется как период, происходящие события в процессе которого закладывают фундамент для второго цикла
· 2 цикл делится на две части
· В первой части второго цикла события первого цикла повторяются N (неопределенное) количество раз до события X, то есть «зеркала»
· Зеркало характеризуется тем, что все события после него носят обратный характер
· Во второй части второго цикла события первой части второго цикла разворачиваются в обратном порядке
· В заключительном 3 цикле события 1 цикла повторяются в обратном порядке
Для упрощенного понимания этой схемы так же вернемся к терминологии двоичной системы счисления. Представим перед собой ячейку информации, например 1 байт. В одном байте находится 8 бит, т.е. 8 ячеек, каждая из которых может иметь значения 1 или 0.
Таблица 1
По принципу зеркала мы вводим в эту схему понятие единицы, т.е. 1 и далее начинаем продвигать ее в условно пустые ячейки, получая следующее:
Таблица 2
Мы видим матрицу, в которой каждая ячейка в конечном итоге (исключая промежуточные варианты) заполняется 1, то есть информацией.
Как только происходит полное заполнение этих ячеек (при повторении N раз), происходит событие X (зеркало), которое запускает обратный процесс, то есть:
Таблица 3
Таким образом мы возвращаемся в изначальное положение, «очищая» свое множество, превращая его в первоначальное «пустое множество».
Схема с зеркалом не будет полной без следующего уточнения:
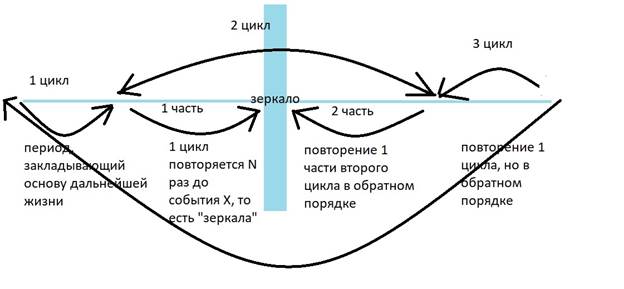
Рисунок 3
Стрелка как бы «возвращает» нас в начало, то есть создает опять же цикл. Который вновь повторяется какое-то M количество раз.