Тема 1. Аксиомы стереометрии и следствия из них.
Стереометрия - это раздел геометрии, в котором изучаются фигуры в пространстве. Основными фигурами являются: точка, прямая и плоскость.
· Точки обозначаются прописными буквами: А, В, С…
· Прямые обозначаются одной строчной или двумя прописными буквами: а или АВ.
· Плоскости обозначаются греческими буквами:  …
…
В основе каждого курса геометрии лежат аксиомы - утверждения, которые принимаются без доказательств. С помощью этих утверждений определяются остальные объекты и их свойства.
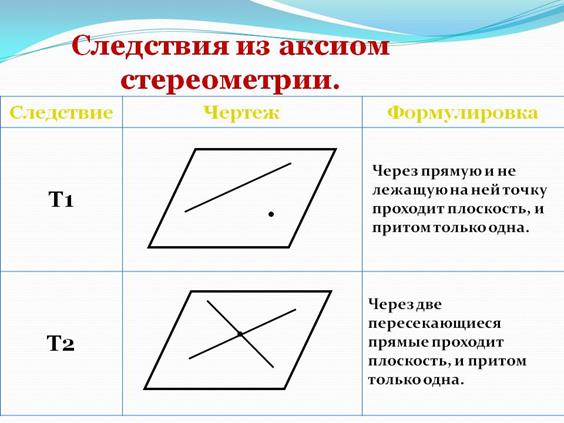
Аксиомы стереометрии.
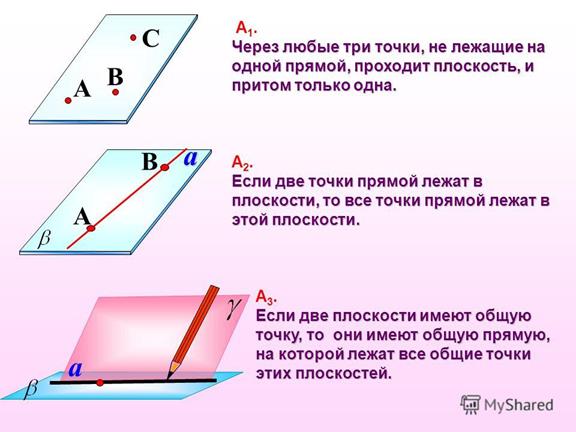
Некоторые обозначения
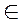 - принадлежит (точка)
- принадлежит (точка)
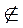 - не принадлежит
- не принадлежит
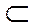 - лежит (прямая)
- лежит (прямая)
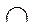 - пересекает
- пересекает
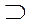 - проходит через
- проходит через
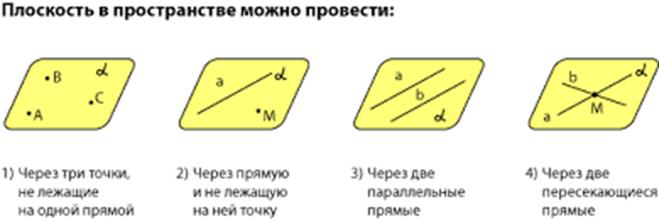
Практические упражнения:
Из учебника «Геометрия 10-11» (автор Л.С. Атанасян): стр 7-8, задачи № 1,2.
Тема 2. Взаимное расположение прямых в пространстве
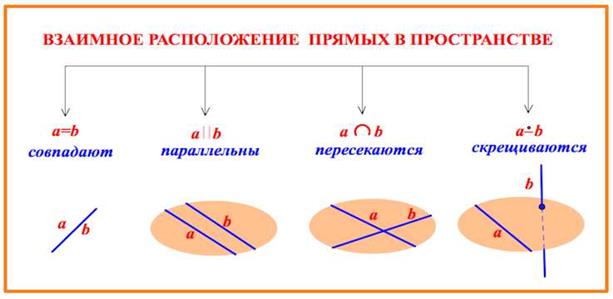
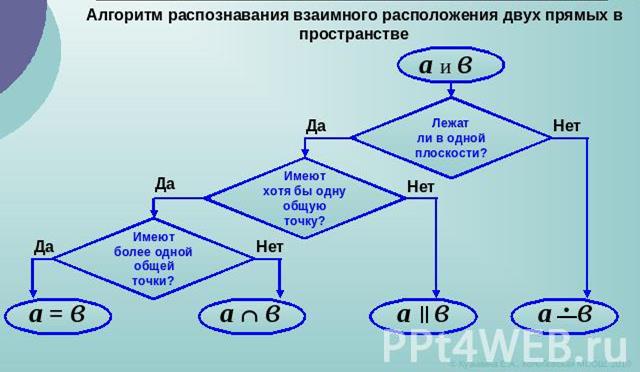
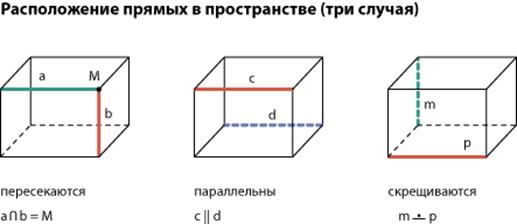
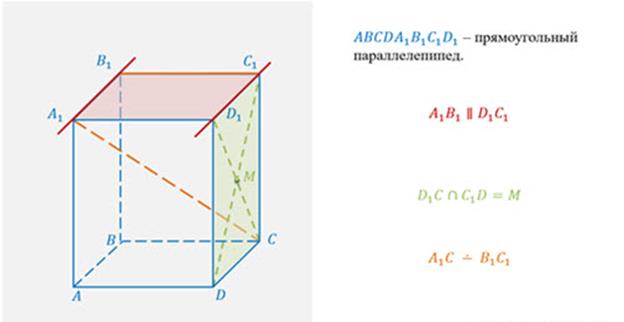
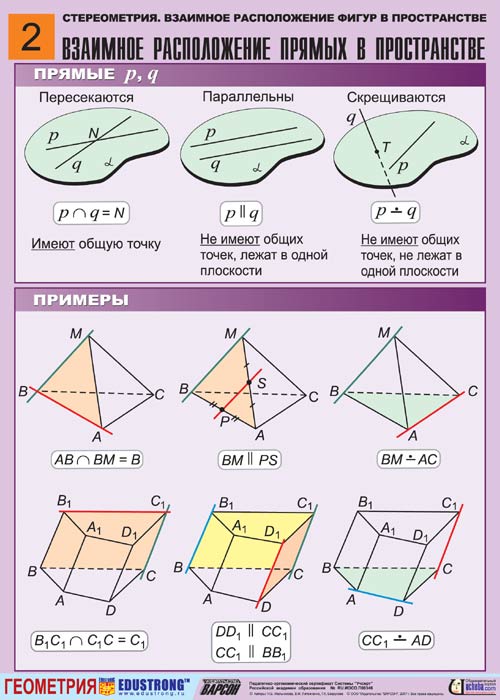
Упражнения:
Выполните чертёж по условию. Дано: АВСД – параллелограмм, О  (АВСД),
(АВСД),
М – середина ОД, К – середина ОС. Определите взаимное расположение прямых:
А) АВ и МК
Б) ОМ и ДМ
В) МК и АД
Г) АО и МД
Д) АВ и ОС
Тема 3. Скрещивающиеся прямые.
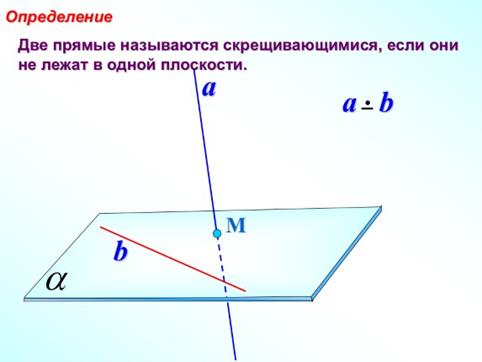
Теорема
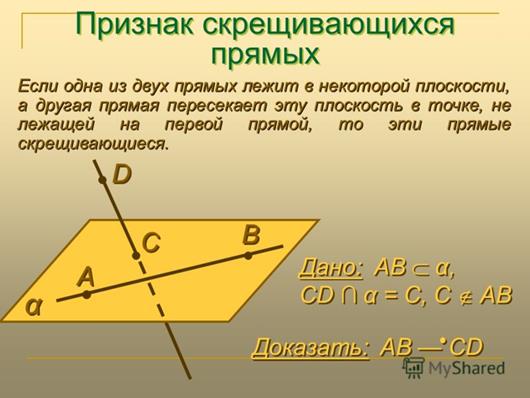
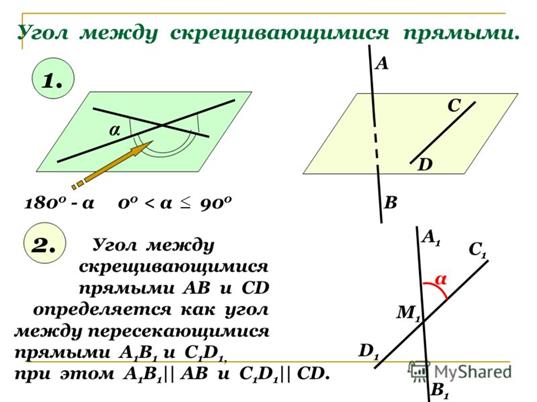
Пример. Дано: АВСД – параллелограмм, 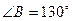 , О
, О  (АВСД), М – середина ОД, К – середина ОС. (рис1). А) Доказать: МК
(АВСД), М – середина ОД, К – середина ОС. (рис1). А) Доказать: МК 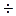 АД. (прямые скрещивающиеся).
АД. (прямые скрещивающиеся).
Б) Найти угол между МК и АД.
А) Доказательство: МК 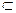 (ДОС), АД
(ДОС), АД  (ДОС)=Д, Д
(ДОС)=Д, Д  МК
МК 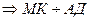 - по признаку скрещивающихся прямых.
- по признаку скрещивающихся прямых.
Б) Решение: МК  СД, значит угол между МК и АД соответственно равен
СД, значит угол между МК и АД соответственно равен
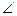 АДС=
АДС= 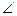 В=130
В=130 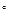
О
|

Тема 4. Параллельность прямой и плоскости.
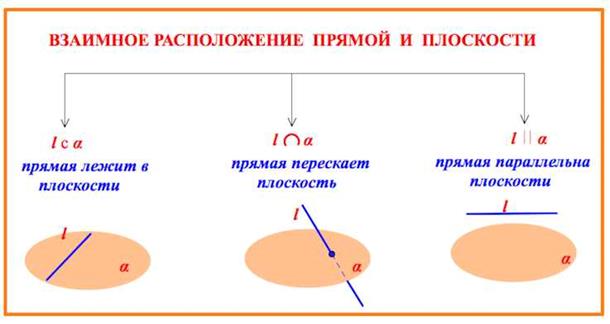
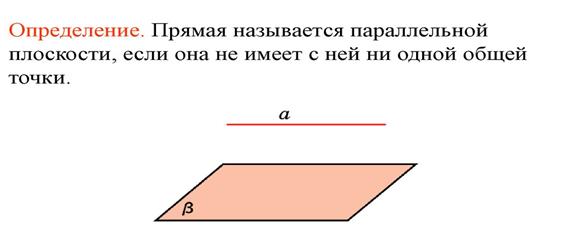
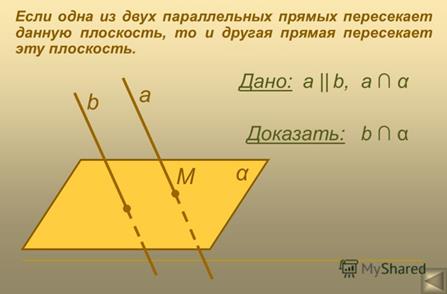
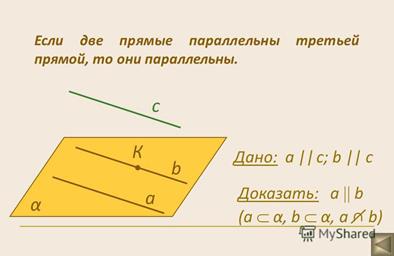
Теорема
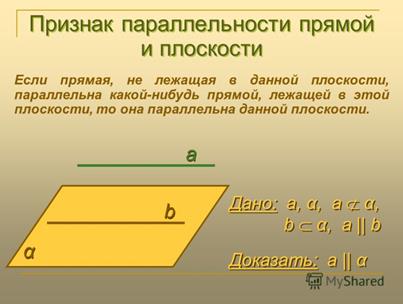
Следствия из теоремы:
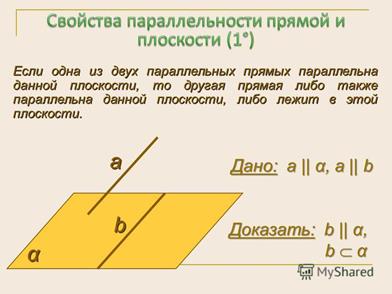
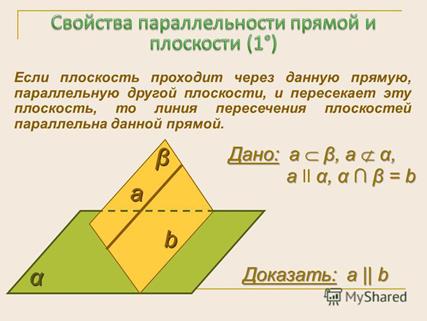
ПРИМЕР. Дано: АВСД – параллелограмм, О  (АВСД), М – середина ОД,
(АВСД), М – середина ОД,
К – середина ОС. (рис1). Доказать: МК 
 (АВСД).
(АВСД).
Док-во: МК 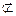 (АВСД), МК
(АВСД), МК  СД (так как средняя линия
СД (так как средняя линия 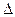 ДОС), СД
ДОС), СД 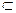 (АВСД)
(АВСД) 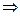
МК  (АВСД) – по признаку параллельности прямой и плоскости.
(АВСД) – по признаку параллельности прямой и плоскости.
Практические упражнения:
Из учебника «Геометрия 10-11» (автор Л.С. Атанасян): стр 13, № 22, 23, 24.
Тема 4. Параллельность плоскостей.
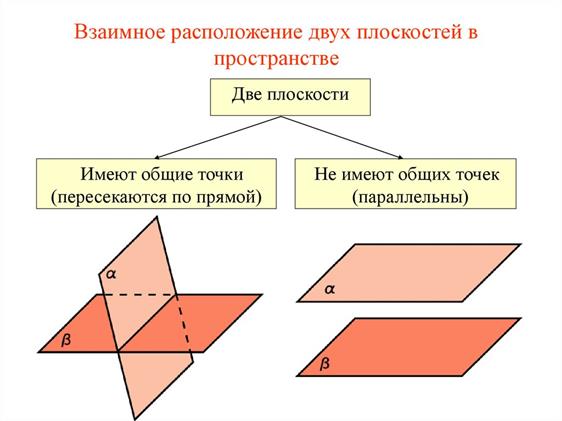
Теорема.

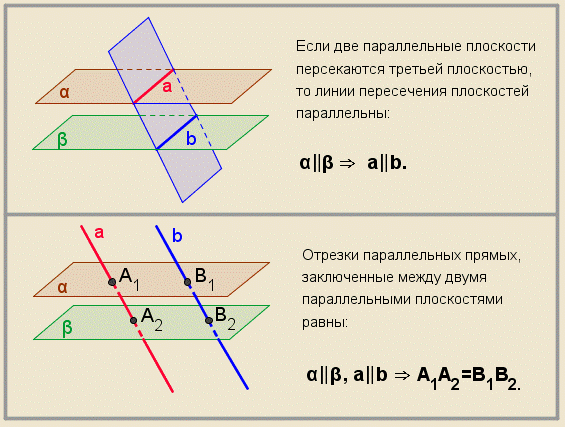
Свойства параллельных плоскостей
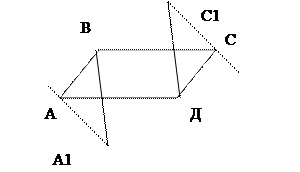
ПРИМЕР. Дано: АВСД- параллелограмм, АА1  СС1. Доказать: (АА1В)
СС1. Доказать: (АА1В)  (СС1Д).
(СС1Д).
Док-во: АА1  СС1 (по условию), АВ
СС1 (по условию), АВ  СД(т.к АВСД- парал-м),
СД(т.к АВСД- парал-м),
(АА1 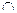 АВ)
АВ) 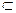 (АА1В), (СС1
(АА1В), (СС1 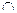 СД)
СД) 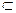 (СС1Д)
(СС1Д) 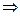 (АА1В)
(АА1В)  (СС1Д)- по признаку параллельности плоскостей.
(СС1Д)- по признаку параллельности плоскостей.
Практические упражнения:
1. Через вершины А и С параллелограмма АВСД проведены параллельные прямые АА1 и СС1, не лежащие в плоскости параллелограмма. Докажите, что (А1АВ)  (С1СД).
(С1СД).
2. Параллелограммы АВСД и АВС1Д1 (общее ребро АВ) не лежат в одной плоскости. Докажите, что (СВС1)  (ДАД1).
(ДАД1).
3. Из учебника «Геометрия 10-11» (автор Л.С. Атанасян): стр 22, № 54(а).
Тема 5. Тетраэдр и параллелепипед.
Самостоятельное изучение из учебника «Геометрия 10-11» (автор Л.С. Атанасян). стр 24-26. Сделать конспект в тетрадь (состав, основные понятия и свойства фигур).
Практические упражнения.
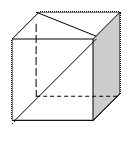
Рис 1.
1. ДАВС – тетраэдр (АВС- основание), М – середина АВ, N – середина ВС.
Докажите, что МN  (ДАС).
(ДАС).
2. (по рис 1) АВСД- нижнее основание, А1В1С1Д1 –верхнее основание соответственно.
Найдите: а) (АДД1) 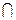 (АВВ1) =.. Б) АВ1
(АВВ1) =.. Б) АВ1 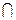 (ВСД) = …
(ВСД) = …
В) Каким плоскостям принадлежит точка А? Г) В каких плоскостях лежит прямая ДД1?
3. (по рис 1). Определите взаимное расположение прямых:
а) АД и В1С1 б) В1С1 и ДС в) АД1 и АД г) АД и Д1С1 д) АВ и ДС.
4. (по рис 1). Найдите угол между АД и Д1С1, если 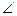 АДС = 140
АДС = 140 
5. Параллелограмм АВСД и трапеция МВСК лежат в разных плоскостях и имеют общую сторону ВС. А) Докажите, что МК  (АДС)
(АДС)
б) Докажите, что прямые МК и ДС скрещивающиеся.
В) Найдите угол между МК и ДС, если  А = 60
А = 60