МИНОБРНАУКИ РОССИИ
федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Санкт-Петербургский государственный технологический институт (технический университет)»
(СПбГТИ(ТУ))
Факультет Информационных технологий и управления
Кафедра Систем автоматизированного проектирования и управления
ОТЧЕТ
По дисциплине
«Планирование исследований и анализ экспериментальных данных»
Вид занятия: самостоятельная работа
Тема №2: Формирование структуры статистических связей переменных на базе корреляционного анализа
Шепелев А.С.
Группа № 424
Проверил: проф. Большаков А.А.
Дата: 06.03.15
Оценка: отлично
Санкт-Петербург
2015
Оглавление
Введение. 3
Методика решения. 3
Основная часть. 3
Заключение. 6
Библиографический список. 7
Введение
Цельработы – определить связи между случайными величинами на входе и на выходе и проверить гипотезу о том, что коэффициент корреляции значимо отличается от 0. Методика решения задачи содержится в [1].
Методика решения
1. Для определения связи переменных служит коэффициент корреляции, который определяется по формуле(1):
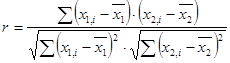 , (1)
, (1)
где x1 и x2 – заданные переменные, а 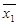 и
и 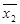 – их средние значения. Коэффициент является линейным и изменяется в пределах [-1; 1].
– их средние значения. Коэффициент является линейным и изменяется в пределах [-1; 1].
2. Чтобы доказать гипотезу, что коэффициент корреляции значимо отличается от 0 вычисляется значение тестовой статистики по формуле (2):
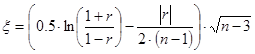 , (2)
, (2)
которая сравнивается с табличным значением критерия распределения Стьюдента при бесконечном числе опытов и вероятностью 0.95. Он равен 1.96.
3. В случае, если тестовая статистика больше критерия Стьюдента, то коэффициент корреляции значимо отличается от 0, в противном случае – не значимо. Формулы взяты из [2].
Основная часть
1. В задаче берутся 3 физические величины одного объекта – человека: возраст, вес и количество невусовна теле. Обозначим их, соответственно, x 1, x 2 и y. Проводятся 20 экспериментов и получившиеся данные заносятся в таблицу 1.
Таблица 1 –Экспериментальные данные
| Параметр | ||
| x 1 | x 2 | y |
2. Необходимо рассчитать средние значения для каждого из параметров:
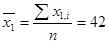 ;
;  и
и 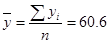 .
.
Образуем всевозможные пары значений результатов измерений и для каждой пары найдём коэффициент корреляции, используя формулу (1).
Между x 1и y: 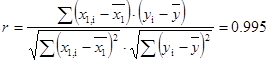 .
.
Между x 2и y: 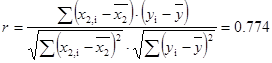 .
.
Между x 1и x 2: 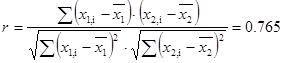 .
.
Из формулы (1) видно, что при перестановке переменных местами, результат остается прежним. Об этом свидетельствует произведение в числителе и квадраты в знаменателе. Следовательно, для пар { x 2; x 1}, { y; x 1} и { y; x 2} значения уже вычислены.
Для связей переменной с собой, коэффициент корреляции равен 1.
Получившиеся результаты заносятся в таблицу 2.
Таблица 2 – Корреляционная матрица
| x 1 | x 2 | y | |
| x 1 | 0.765 | 0.995 | |
| x 2 | 0.765 | 0.774 | |
| y | 0.995 | 0.774 |
Доказывается гипотеза о том, что коэффициент корреляции значимо отличается от 0.
Считается тестовая статистика по формуле (2):
Пара { x 1; y } и { y; x 1}:
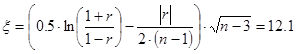
Пара { x 2; y } и { y; x 2}:
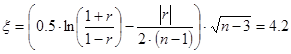
Пара { x 1; x 2} и { x 2; x 1}:
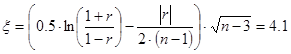
3. Сравниваем каждое из этих значений с критерием Стьюдента, 12.1>1.69, 4.2>1.6, 4.1>1.69, получаем, что все коэффициенты корреляции значимо отличаются от 0.
Заключение
Определенызначения коэффициентов корреляции, показывающие зависимости исходных величин, которые наглядно представлены в таблице 1. Гипотеза о том, что коэффициент корреляции значимо отличается от 0 доказана, так как все полученные коэффициенты значимо отличаются от 0.
Библиографический список
1 Белов, Е. А. Расчетные задания по математической статистике: методические указания / Е. А. Белов, В. О. Поляков. – СПб.:СПбГТИ(ТУ), 2001. – 38с.
2 Статистика в аналитической химии [Электронный ресурс]– Режим доступа:https://www.chemstat.com.ru, свободный. – Загл. с экрана.