Перенесем на функции нескольких переменных основные понятия дифференциального исчисления функций одной переменной, а, именно, понятия производной и дифференциала. Для функций нескольких переменных придется определять несколько производных, точнее, столько производных, сколько независимых переменных у данной функции.
Пусть функция 
определена в некоторой окрестности точки 
. Придадим переменной 
приращение 
, а значение переменной 
менять не будем, то есть перейдем на плоскости от точки к точке 
( таково, что точка 
принадлежит окрестности точки М). При этом значение функции 
также изменится. Назовем это изменение частным приращением функции 
по переменной : 
.
Аналогично можно составить частное приращение по переменной :
.
Определение. Если существует конечный предел
,
то он называется частной производной по переменной (по переменной ) от функции в точке .
Частные производные обозначаются одним из следующих символов: 
, или 
, или 
, или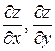 
. Если нужно явно указать, в какой точке вычислена частная производная, то пишут, например, так: 
, или 
.
Из определения следует, что частная производная функции двух переменных равна обычной производной функции одной переменной, полученной при условии, что вторая независимая переменная сохраняет постоянное значение. Следовательно, правила и формулы отыскания частных производных те же, что и правила и формулы обычных производных функций одной переменной.
Найти частные производные следующих функций:
Пример 1. 
.
Функция определена в области 
. Фиксируя переменную , находим частную производную по переменной : 
.
Фиксируя переменную , получаем частную производную по переменной :
.
Пример 2. 
.
Функция определена при условии 
. Фиксируя переменную , находим частную производную по переменной : 
.
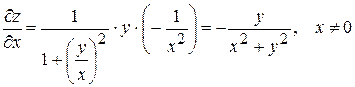Фиксируя переменную , получаем частную производную по переменной :
.
Пример 3. 
. Доказать, что 
.
Функция определена при 
. Найдем частные производные:
.
.
Проверим, справедливо ли равенство, для этого вычислим величину выражения 
, подставив туда найденные частные производные:
,
то есть действительно равенство верно.
Пример 4.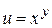 
. Доказать, что 
.
Функция определена при .
. Вычислим:
.
Следовательно, равенство верно.
Можно ввести понятие частной производной порядка выше первого. Так как частные производные 
и 
какой-либо функции двух переменных 
сами являются, вообще говоря, функциями двух переменных, то от них опять можно брать частные производные по и . Результат дифференцирования называется частной производной второго порядка (или просто второй частной производной). Если от взять частную производную по , то есть вычислить 
, то результат обозначается 
или 
. От частной производной можно взять частную производную по : 
. Результат дифференцирования называется смешанной частной производной второго порядка и обозначается: 
или 
.
Таким же образом можно вычислить частные производные второго порядка 
и 
, полученные от дифференцирования частной производной по и по соответственно.
Справедливо утверждение: если смешанные частные производные, отличающиеся порядком дифференцирования, непрерывны, то они не зависят от порядка дифференцирования, то есть 
.
Пример 5. Найти частные производные второго порядка функции 
.
Найдем частные производные первого порядка:
;
.
Находим частные производные от этих:
;
;
.
Так как смешанная производная второго порядка непрерывна на 
, то она не зависит от порядка дифференцирования, то есть .
Можно определить и производные более высоких порядков. Так для функции можно написать восемь частных производных третьего порядка:
(или 
), 
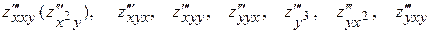, шестнадцать частных производных четвертого порядка и так далее.
Если рассматривать функцию трех переменных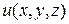 
, то для нее имеем три частные производные первого порядка 
, девять частных производных второго порядка 
и так далее.
Заметим, что смешанные производные любого порядка при условии их непрерывности не зависят от порядка дифференцирования, например 
.