Постановка задачи. Минимизация схемы в булевом базисе сводится к поиску минимальной дизъюнктивной формы, которой соответствует минимальное покрытие. Общее число букв, входящих в нормальную форму, выражается ценой покрытия 
, где 
— число 
- кубов, образующих покрытие данной функции от п переменных. Минимальное покрытие характеризуется наименьшим значением его цены.
Обычно задача минимизации решается в два шага. Сначала ищут сокращенное покрытие, которое включает все -кубы максимальной размерности, но не содержит ни одного куба, покрывающегося каким-либо кубом этого покрытия. Соответствующею дизъюнктивную нормальную форму называют сокращенной, а ее минитермы - простыми импликантами. Для данной функции сокращенное покрытие является единственным, но оно может быть избыточным вследствие того, что некоторые из кубов покрываются совокупностями других кубов.
На втором шаге осуществляется переход от сокращенной к тупиковым дизъюнктивным нормальным формам, из которых выбираются минимальные формы. Тупиковые формы образуются путем исключения из сокращенного покрытия всех избыточных кубов, без которых оставшаяся совокупность кубов еще образует покрытие данной функции, но при дальнейшем исключении любого из кубов она уже не покрывает множества всех вершин, соответствующих единичным значениям функции, т. е. перестает быть покрытием.
Куб сокращенного покрытия, который покрывает вершины данной функции, не покрываемые никакими другими кубами, не может оказаться избыточным и всегда войдет в минимальное покрытие. Такой куб, как и соответствующая ему импликанта, называют экстремалью (существенной импликантой), а покрываемые им вершины - отмененными вершинами. Множество экстремалей образует ядро покрытия, ясно, что при переходе от сокращенного покрытия к минимальному прежде всего следует выделить все экстремали. Если множество экстремалей не образует покрытия, то оно дополняется до покрытия кубами из сокращенного покрытия.
Приведенные определения иллюстрируются на рис. 3.9, где сокращенное покрытие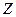 
(см. рис. 3.9а, ) и минимальные покрытия 
(рис. 3.9б) и 
(см. рис. 3.9, б) выражаются следующим образом:
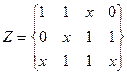
Рис. 3.9 Сокращенное (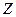) и минимальные покрытия (, ) функции 
(а – сокращенное, б, в - минимальные)
Сокращенная форма представляет собой дизъюнкцию четырех простых импликант, т. е.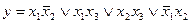 
Экстремалями являются простые импликанты 
и 
,которым соответствуют 1-кубы (
) и (
), а отмеченные вершины - 
и 
или соответственно (100) и (010).
Метод Квайна – Мак-Класки. Этот метод используется в случаях, когда функция задана в дизъюнктивной совершенной форме (или таблицей истинности). Приведение в сокращенной форме осуществляется последовательным применением операций склеивании 
, где 
– конъюнкции переменных, отличных от 
. Множеству конституент единицы, представленных в исходной форме, соответствует совокупность 0-кубов К0, а операции склеивания – объединения двух 0-кубов, которые отличаются только одной координатой. Результатом такого объединения является 1-куб, в котором различные координаты исходных 0-кубов заменены символом 
. Сравнивая попарно все 0-кубы. Получаем множество 1-кубов К1. Применяя к К1 операцию склеивания, находим множество 2-куюов К2 и т. д. Этот процесс продолжается до тех пор, пока получаемое из К s очередное К s+1 не окажется пустым множеством. В результате множество К0 преобразуется в комплекс кубов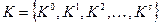 
, причем 
.
Для выделения из 
множества простых импликант 
при каждой операции склеивания необходимо отмечать каким-либо знаком (например, меткой 
) те кубы, которые объединяются в кубы высшей размерности. Очевидно, неотмеченные кубы и образуют множество простых импликант 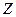. Чтобы уменьшить число сравниваемых пар при операции объединения целесообразно разбить множество К s на классы, в каждом из которых содержаться s -кубы с одинаковым числом единиц (или нулей), и упорядочить эти классы по возрастающему числу единиц. Так как объединяться когут только такие s -кубы, число единиц в которых точно на одну больше или менше, то достаточно ограничится попарным сравнением s -кубов одного класса с s -кубами соседнего.
На втором шаге при извлечении экстремалей и образовании минимального покрытия используется таблица покрытия. Ее строки соответствуют простым импликантам, а столбцы – конституентам единицы дизъюнктивной совершенной нормальной формы данной функции, которые представляются 0-кубами (вершинами) комплекса кубов. В клетку таблицы записывается метка, если простая импликанта в данной строке покрывает вершину в данном столбце. Экстремалям соответствуют те строки таблицы, которые содержат единственную метку в каком-либо столбце. Удаляя строки экстремалей и все ее столбцы, в которых эти строки имеют метки, получаем более простую таблицу. На основе этой таблицы выбираем простые импликанты, которые дополняют выделенное множество экстремалей до минимального покрытия функции.
Пример минимизации функции методом Квайна. Рассмотрим в качестве примера функцию от четырех переменных:
Множество кубов после разбиения и упорядочения записывается следующим образом
Объединяя кубы и отмечая те из них, которые покрываются кубами большей размерности, имеем (слева от фигурных скобок стоят метки, обозначающие операции склеивания):
.
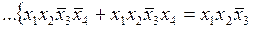
Простым импликантам соответствуют неотмеченные кубы. Составляем таблицу покрытия 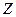, которому соответствует сокращенная форма:
 |
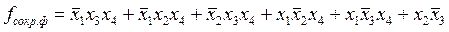
Извлекаем единственную экстремаль (
), которой соответствует минтерм 
(экстремалей в таблице может быть несколько). Экстремаль это строка, имеющая единственную метку в каком либо столбце. Экстремаль забирает за собой все столбцы, в которых она имеет метки (выделены серым цветом). Тогда упрощаем таблицу:
 |
Какие кубы выбрать в качестве дополнительных? В каждом столбце мы должны выбрать по одной метке. Если мы в первом столбце выбираем метку, соответствующую (
), то в третьем столбце также нужно выбрать метку, соответствующему этому же однокубу. Тогда во втором и в четвертом столбцах целесообразно выбрать метку, соответствующую однокубу (
). Выбранные дополнительные однокубы совместно с экстремалью () образуют покрытие функции, минимальная форма которой имеет вид: 
.
Минимизируем эту функцию с помощью карты Карно. Нетрудно заметить, что мы получили тот же результат.
Данная функция имеет две минимальные формы, о чем говорит наличие двух меток в каждом столбце в упрощенной таблице. Если мы выберем в первом столбце метку, соответствующую (
), то в четвертом столбце также нужно выбрать метку, соответствующему этому же однокубу. Тогда во втором мы выберем (
), а третьем - (
). Тогда вторая минимальная форма имеет вид:
На карте Карно контура будут следующими:
Ясно, что первый вариант предпочтительней, т.к. в него входит меньшее количество слагаемых.
Метод сочетания индексов. Заполним таблицу истинности, в которой дополнительные столбцы нечто иное, как коды из всех упорядоченных сочетаний индексов переменных, от которых зависит функция 
Приведем пример для той же функции.
Все коды на строках, заканчивающиеся нулевыми значениями функции, исключаются автоматически. Если эти коды попадают на строки, заканчивающиеся единичными значениями функции, то они также не учитываются. Остаются только те коды, которые расположены на строках с единичным значением функции (эти коды затемнены серым цветом).
 |
Для того чтобы функция приняла значение равное единице, достаточно того, чтобы только какая-нибудь одна импликанта на строке приняла единичное значение.
Прежде всего оставляем минимальную импликанту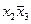 
(10), которая перекрывает единицы в строках 2,3,10,11. Затем обращаемся к 9-ой строке, что отвечает импликанте 
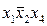(101). Осталось рассмотреть 12, 13 и 14 строки. Общей для них является импликанта 
(011).
3.2. Задание
1. В таблице 1 заданы номера конституент, на которых логическая функция принимает значение, равное единице (номера конституент соответствуют функции 
). Необходимо провести ее минимизацию следующими методами:
- непосредственных преобразований (с использованием законов);
- с помощью n – мерного куба;
- карты Карно;
- таблиц Квайна.
Ррезультаты для всех методов минимизации должны совпасть.
2. Построить логические схемы в базисах {не-или, не-и} для минимальной формы.
Таблица 2.-
| № | Номера конституент 1 | |||||||
| - | ||||||||
| - | ||||||||
| - | ||||||||
| - | ||||||||
| - | ||||||||
| - | ||||||||
3. Логическую функцию вашего варианта табл.2 запишите в СКНФ номерами конституент 0. Как нужно модифицировать методы минимизации чтобы приспособить их к СКНФ? Произведите минимизацию вашей функции, записанной в СКНФ методами Карно и Квайна.
4. В табл.3 задана функция от пяти переменных 
номерами конституент 0 (номера конституент взять из самостоятельно составленной таблицы истинности для функции). Необходимо провести ее минимизацию методом Карно и Квайна (результаты методов минимизации должны совпасть). Построить логические схемы в базисах {не-или, не-и} для минимальной формы.
Таблица 3.-
| № | Номера конституент 0 | |||||||
| - | - | - | - | |||||
| - | - | - | - | |||||
| - | - | - | ||||||
| - | - | - | - | |||||
| - | - | - | - | |||||
| - | - | - | ||||||
| - | - | - | ||||||
| - | - | - | ||||||
| - | - | - | ||||||
| - | - | - | ||||||
| - | - | - | ||||||
| - | - | - | ||||||
| - | - | - | ||||||
| - | - | - | ||||||
| - | - | |||||||
| - | - | |||||||
| - | - | - | ||||||
| - | - | |||||||
| - | - | - | ||||||
| - | - | |||||||
| - | - | - | ||||||
| - | - | - | ||||||
| - | - | - | ||||||
| - | - | |||||||
| - | - | - |
3.3. Контрольные вопросы
3.3.1. Дайте определение логической однородной функции.
3.3.2. Приведите таблицу булевой функции одной переменной.
3.3.3. Какая операция (закон) лежит в основе всех методов минимизации.
3.3.4. Дайте определение логического элемента. Что такое базис?
Лабораторная работа № 4
Тема: «Конечные автоматы с памятью»
Цель: Приобретение практических навыков синтеза конечных автоматов.
4.1. Теоретические сведения [1].
Основные определения.
Комбинационные схемы - логические схемы, значения выходных переменных которых определяются только комбинацией значений переменных на входах в данный момент времени.
Если входные и выходные принимают значения из конечных алфавитов, то к омбинационная схема называется конечным автоматом.
Пусть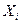 
– алфавит входной переменной , а 
– алфавит выходной переменной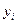 
. Конечный автомат с n входами и m выходами характеризуется входным алфавитом 
и выходным алфавитом 
, причем символами входного алфавита служат слова 
длины n, а символами выходного алфавита – слова 
длины m, где 
и 
.
Особого внимания заслуживают конечные автоматы с двузначным структурным алфавитом, зависимость между входными и выходными переменными которых выражаются булевыми функциями. Их значение обусловлено тем, что любая информация может быть представлена в двоичных кодах (двоично-десятичные коды чисел и т. п.). В то же время при технической реализации автоматов используются преимущественно двоичные элементы и двузначная логика.
В реальных условиях сигналы представляются непрерывными функциями времени, чтобы новые значения на входах появлялись после окончания переходных процессов, связанных с предыдущими значениями. При рассмотрении логической структуры автоматов обычно отвлекаются от существа этих процессов и считают, что переменные изменяются непрерывно, а мгновенно в некоторые моменты времени, называемые тактами. Интервалы между тактами могут быть различными, но без потери общности их можно терять равными 
. Предполагается, что тактовые моменты 
определяются синхронизирующими сигналами. Таким образом, вводится понятие дискретного автоматного времени 
, причем переменные зависят не от физического времени, а от номера такта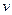 
, т. е. вместо непрерывной функции 
рассматриваются дискретные значения 
.
Состояния. Кроме входных и выходных переменных, можно выделить некоторую совокупность промежуточных переменных, которые связаны с внутренней структурой автомата. В комбинационных схемах промежуточные переменные непосредственно не участвуют в соотношениях вход – выход. Напротив, выходные функции последовательностных схем в качестве своих аргументов, кроме входных переменных, обязательно содержат некоторую совокупность промежуточных переменных 
, характеризующих состояние схемы. Набор всех возможных состояний, которые присущи данной схеме, называются множеством состояний. Если 
– конечные алфавиты переменных состояния , то множество состояний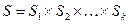 
также является конечным множеством.
Строгое определение понятия состояния связывается с той ролью, которое оно играет при описании конечных автоматов. Во-первых, значения совокупности выходных переменных на v -м такте 
однозначно определяется значениями входных переменных 
и состоянием 
на том же такте, т. е. 
. Во-вторых, состояние 
в следующем 
-м такте однозначно определяется выходными переменными 
и состоянием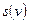 
в предыдущем такте, т. е. 
.
Таким образом, состояние конечного автомата в любой тактовый момент характеризуется значениями такой совокупности переменных, которая вместе с заданными значениями входных переменных позволяет определить выходные переменные в данный тактовый момент и состояние в следующий тактовый момент.
Ясно, что последовательные схемы должны обладать способность сохранять предыдущее состояние до следующего такта, в связи с чем их называют также автоматами с памятью или последовательностными машинами. В качестве памяти могут использоваться элементы задержки, на выходах которых повторяются входные воздействия со сдвигом во времени на интервал между тактами . Широко применяются также различные запоминающие элементы, например, триггеры, способные сохранять состояния на выходах то тех пор, пока оно не изменяется в результате воздействия на их входы.
Типы конечных автоматов. В технике с понятием автомата обычно связывается некоторое устройство, способное выполнять определенные функции без вмешательства человека или с его ограниченным участием. Однако такое понятие является слишком узким. В широком смысле конечный автомат – это математическая модель, отображающая физические или абстрактные явления самой разнообразной природы. Такая модель успешно используется как в технике (проектирование электронных вычислительных машин, систем управления и связи), так и в других областях – психологии и физиологии (исследования деятельности нервной системы человека и простейших видов поведения животных), лингвистике (анализ синтаксиса русского, английского и других языков, расшифровка древних рукописей), теории и практике административного управления и т. п. Универсальность теории автоматов позволяет рассматривать с единой точки зрения различные объекты, устанавливать связи и аналогию между ними, переносить результаты из одной области в другую.
Конечный автомат М определяется двумя характеристическими функциями:
;
,
называемыми соответственно функцией переходов и функцией выходов. Общая блок-схема конечного автомата (рис. 4.1) может быть представлена в виде комбинационной схемы, реализующей характеристические функции 
и 
, и памяти, сохраняющая на один такт предыдущее состояние автомата.
 |
Рис.4.1 Блок-схема конечного автомата
В определении автомата участвует три конечных множества 
, 
, 
и две функции и , задающими некоторые отношения между элементами этих множеств.
Приведенное вначале этого параграфа определение связывают обычно с автоматом первого рода, называемым также автоматом Мили. Если выходные переменные являются функцией только состояния, то имеем автомат второго рода или автомат Мура.
Для комбинационных схем функция перехода не имеет смысла, а функция выходов вырождается к виду 
. Их называют автоматами без памяти или тривиальными автоматами. Мы рассматривали такой тривиальный автомат на примере устройства, решающего задачу принятия решения при голосовании трех человек.
Представления конечных автоматов. Автомат может быть задан различными способами, например, путем словесного описания его функционирования или перечислением элементов множеств , , , с указанием отношений между ними. При анализе и синтезе конечных автоматов используют стандартные формы представления: таблицы, графы и матрицы. Элементы множества , , удобно пронумеровать порядковыми числами, начиная с нуля, например: 
, 
и 
. Тогда характеристические функции и можно представить двумя таблицами, строки которых соответствуют состояниям, а столбцы – входам. Первая таблица, называемая таблицей переходов, соответствует функции 
, и ее клетки заполняются номерами состояний 
, в которые переходит автомат при воздействии , и состоянию 
в данный тактовый момент. Вторая таблица, называемая таблицей выходов, соответствует функции 
, и ее клетки заполняются номерами выходов 
в данный тактовый момент, которые соответствуют воздействию и состоянию в тот же момент. Например, для заданных множеств , , такие таблицы могут иметь вид:
|
| ||||||||||
|
| |||||||||
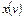
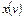
Обе таблицы можно объединить в общую таблицу переходов, если условиться записывать в клетках пары чисел (номера следующего состояния в числителе и номер выхода в знаменателе), т. е.
|
| ||||
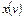
| 3/0 3/1 3/1 3/0 | 2/0 2/0 2/0 0/0 | 1/0 1/0 2/1 0/1 | 3/0 3/1 3/1 1/1 |
Граф автомата строится таким образом, что его вершины соответствуют состояниям, а направленные дуги обозначаются как дизъюнкцию входов, под воздействием которых совершается переход из одного состояния в другое по направлению дуги. В знаменателях записываются номера входов, соответствующие этим переходам.
На рис. 4.2 показан граф, построенный в соответствии с приведенной выше таблицей переходов. Так как из состояния 0 автомат переходит в состоянии 1,2 и 3, то из вершины 0 графа исходят дуги к вершинам 1, 2 и 3. При этом переход в состояние 1 совершается под воздействием 2 и ему соответствует выход 0, поэтому дуга из вершин 0 и 1 помечается как 2/0. Переход в состояние 2 совершается под воздействием 1 и ему соответствует выход 0, поэтому дуга из вершины 0 в 2 помечается как 1/0. Переходы в состояние 3 совершаются под воздействиями 0 и 3 и им обоим соответствует выход 0, поэтому дуга из вершины 0 в 3 помечается как дизъюнкция 
. Аналогично определяются и другие дуги графа. Так рассматриваемый автомат переходит из состояния 2 в 2 под воздействиями 1 и 2, которым соответствуют выходы 0 и 1. Следовательно, петля при вершине 2 помечается как 
.
Синтез конечных автоматов. Реализация конечных автоматов сводится к синтезу соответствующей комбинационной схемы, преобразующей входные переменные и в выходные переменные 
и в соответствии с заданными характеристическими функциями и . Для сохранения состояния до следующего такта в цепь обратной связи вводится необходимое количество элементов памяти.
При реализации автоматов в двоичном структурном алфавите необходимо закодировать состояние схемы и представить характеристические функции в виде булевых функций двоичных переменных. Такое кодирование можно осуществить преобразованием общей таблицы перехода автомата к таблице соответствия в двоичном структурном алфавите. Если элементы множеств , и пронумерованы порядковыми числами, начиная с нуля, то им соответствуют коды, представляющие собой двоичные эквиваленты этих чисел. Например, для автомата, заданного в предыдущем пункте, таблицу переходов можно преобразовать к виду:
|
| |||||||||||||||||||
|
|
Заменяя десятичные числа их двоичными эквивалентами, читаемыми сверху вниз, получаем таблицу соответствия. В которой значения функций и представлены двоичными кодами:
| |||||||||||||||||||
| |||||||||||||||||||
Отсюда видно, что комбинационная схема должна иметь четыре входа, соответствующие входным переменным 
, 
и переменным состояния 
, 
, а также три выхода, соответствующие переменным состояния 
, 
и выходной переменной 
. Синтезировав комбинационную схему, соответствующую полученной таблице и введя два элемента задержки ЭЗ1 и ЭЗ2, получим структурную схему автомата (рис. 4.3).
Рис. 4.3 Структурная схема конечного автомата
Моделирование памяти. Триггер - класс электронных устройств, обладающих способностью длительно находиться в одном из двух или более устойчивых состояний и чередовать их под воздействием внешних сигналов. Каждое состояние триггера легко распознаётся по значению выходного напряжения. По характеру действия триггеры относятся к импульсным устройствам - их активные элементы (транзисторы, лампы) работают в ключевом режиме, а смена состояний длится очень короткое время.
Отличительной особенностью триггера как функционального устройства является свойство запоминания двоичной информации. Под памятью триггера подразумевают способность оставаться в одном из двух состояний и после прекращения действия переключающего сигнала. Приняв одно из состояний за «1», а другое за «0», можно считать, что триггер хранит (помнит) один разряд числа, записанного в двоичном коде.
Характеристическое уравнение триггера: 
, где
- значение выходной переменной на (
) - м такте;
- знач