Критерий полноты системы функций алгебры логики.
Опр: Функцией алгебры-логики 
, зависящей от переменных 
, будем называть функцию
Опр: Пусть имеется непустая система функций алгебры-логики B, будем говорить что система B полная, если каждая функция алгебры логики может быть представлена в виде формулы над B.
Примеры полных систем:
-
– множество всех функций алгебры логики. - B –
Теорема: О полноте.
Утверждение: О несамодвойственной функции.
Пусть 
, тогда путём подстановки вместо независимых переменных функции вида 
или 
можно получить из функции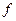 
константу.
Утверждение: О немонотонной функции.
Пусть функция 
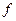, тогда путём подстановки вместо констант и функций вида можно получить из отрицание .
Утверждение: О нелинейной функции.
Пусть функция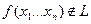 
, тогда путём подстановки вместо независимых переменных функций вида 
или 
и констант, а также путём возможного перехода к самой функции можно получить из функции 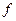конъюнкцию.
Критерий полноты:
Пусть 
, B – непустая система функций из ,
Тогда B – полная ó B – не содержится целиком ни в одном из следующих классов: 
Замечание:
класс всех булевых функций , сохраняющих константу 0. Т.е. функций для которых выполнено 
.
класс всех булевых функций , сохраняющих константу 1. Т.е. функций для которых выполнено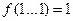 
.
класс самодвойственных функций, т.е. функций 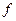на 
таких, что 
.
М – множество всех монотонных функций. L – класс линейных функций.
Док-во:
(=>) Пусть B – полная система и B содержится в каком-то из перечисленных классов, т.е. 
, но тогда мы получи следующую цепочку включений: 
. Получили противоречие.
(<=) Пусть B – не содержится ни в одном из перечисленных классов, тогда
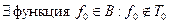
Эти функции необязательно различны. Покажем, что подмножество 
является полной системой (воспользуемся теоремой о полных системах).
Шаг 1. Получение констант.
Покажем, что константы 0 и 1 могут быть представлены в виде формулы над 
. Рассмотрим функции 
возможны 4-е случая:
1) 
, 
2) , 
3) 
,
4) ,
Введём вспомогательные функции: 
и 
В случае 1) получим:
(т.к. 
),
,
, 
Т.о. отрицание представляется в виде формулы над , но тогда использую функцию 
по утверждению о несамодвойственной фцнкуции, можно получить в виде формулы над какую-нибудь константу 
(0 или 1). Вторая константа 
получается из с помощью уже полученного отрицания, т.е. 
.
В случае 2) получим:
, 
т.к.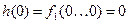 
, 
В случае 3) получим:
, 
, 
В случае 4) получим:
, 
, 
Шаг 2. Получение отрицания.
Если отрицание не было получено на первом шаге (случай 3), то представим его в виде формулы над , используя функцию 
и это можно сделать благодаря утверждению о немонотонной функции.
Шаг 3. Получение конъюнкции.
Конъюнкцию можно получить из функции 
по утверждению о нелинейной функции. Т.о. мы получили, что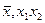 
представляются в виде формулы над , а т.к. система 
- полная, то по теореме о полных системах мы получили, что и - полная и =>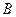 
- полная.
Примеры полных систем функций к-значной логики с доказательством полноты.
Опр: Система функций 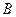К -значной логики наз. полной, если замыкание совпадает со всеми 
, т.е:
Теорема: О полных системах.
Пусть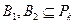 
для которых выполняются условия:
1) 
– полная система;
2) Каждая функция 
Тогда система 
– полная.
Теорема: Пример полной системы к-значной логики.
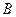– система функций, состоящая: 
, тогда эта система полна.
Док-во:
Рассмотрим систему 
– эта система полная. Выразим каждую функцию этой системы через функции системы .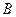
Шаг 1. Получение константы. Рассмотрим функции:
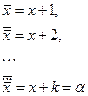
Очевидно, что эти функции 
и рассмотрим функцию:
=> 
. Используя отрицание, получим из константы
k-1 все остальные константы: 
Шаг 2. Получение функций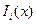 
.
, рассмотрим функцию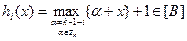 
Если 
, то среди элементов 
есть элемент 
, но тогда => 
, но тогда 
, если 
, то 
и => 
, т.е. 
Шаг 3. Получение функций 
.
Рассмотрим функция 
Если 
, то 
, тогда 
тогда 
Если , то 
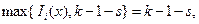, тогда 
тогда 
=>
Шаг 4. Получение произвольной функции от одной переменной.
Рассмотрим произвольную функцию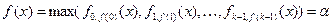 
Шаг 5. Получение конъюнкции.
На 4-ом этапе мы получили все функции от одной переменной в виде формулы над 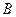, в частности отрицание тоже представляется в виде формулы над 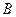,но тогда конъюнкцию можно получить следующим образом: 
=> система полная по теореме о полной системе.