Леммы: о свойствах существенных функций.

Лемма 1: Пусть – существенная функция, принимающая значений. Пусть – её существенная переменная. Тогда найдутся два таких набора и что

и принимает значение, отличное и от и от

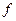Лемма 2: Пусть – существенная функция, принимающая значений, то найдутся n подмножеств множества таких, что и на множестве наборов т.е. на функция принимает 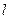значений.

Лемма 3: Пусть – существенная функция, принимающая значений. Тогда найдётся квадрат (* – далее), на котором 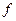принимает либо более двух значений, либо два значения, причём одно из них только в одной его точке.

Теорема: Пусть система B функций из , содержит все функции одной переменной, принимающие не более k – 1 значений. Тогда для полноты системы B необходимо и достаточно, чтобы B содержало существенную функцию , принимающую все к значений.

Док-во: (Н е о б х о д и м о с т ь)

Пусть B – полная система. Предположим, что B не содержит существенной функции, принимающую все к значений. Очевидно, что из B нельзя получить существенной функции, принимающей все к значений. Мы пришли к противоречию. Значит B содержит существенную функцию, принимающую все к значений.

(Д о с т а т о ч н о с т ь)

Пусть B удовл. условию теоремы и содержит существенную функцию , принимающую все к значений. Покажем, пользуясь индукцией, что B полна.

1) Б а з и с и н д у к ц и и.

Покажем, что из B можно получить все функции из , принимающие два значения.

На основании леммы 3 найдётся квадрат:

(*)

где на котором функция 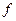принимает не менее двух значений, причём одно из них, , – в одной точке. Возьмём функцию 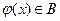такую, что:

Пусть . Функция на квадрате принимает два значения, 0 и 1, причём значения 0 в одной точке; обозначим её . Осуществляя неполную нормировку так чтобы (0,0) отображалось в , а квадрат {(0,0)(0,1)(1,1)(1,0)} – в указанный выше квадрат, получим функцию 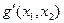, где , . Функция 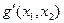, очевидно есть максимум на мн-ве {0,1}x{0,1}. Обозначим её через . Т.к. система содержит функции , где

, то есть минимум на мн-ве {0,1}x{0,1}. Пусть , произвольная функция, принимающая два значения, 0 и 1; тогда

Таким образом, функция может быть получена из системы B. Так как B содержит все функции одной переменной, принимающие любые два значения, то мы можем также получить из B все функции, принимающие любые два значения.

2) Пусть из B построены все функции, принимающие не более значений, . Покажем что тогда можно построить все функции из , принимающие l значений.

Возьмём функцию . На основании леммы 2 найдутся n подмножеств и на 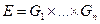функция 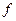принимает 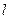значений . Пусть эти значения принимаются соотв. на наборах из :

т.е.

Покажем что их системы B можно построить произвольную функцию , принимающую значения

В самом деле, функцию можно задать при помощи таблицы 1, в которой . Определим функцию так, как указано в таблице 2.

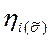
Таблица 1 Таблица 2

Тогда ибо

Имея все функции с заданными 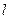значениями можно в случае получить при помощи функций одной переменной, принимающих менее k значений, остальные функции с 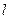значениями. Таким образом применяя этот приём мы дойдём до 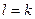, и тогда построим все функции из .