Элементы математической логики.

 

Математическая логика – разновидность формальной логики, т.е. науки, которая изучает умозаключения с точки зрения их формального строения.

 

Определение. Высказыванием называется предложение, к которому возможно применить понятия истинно или ложно.

 

В математической логике не рассматривается сам смысл высказываний, определяется только его истинность или ложность, что принято обозначать соответственно И или Л.

*Замечание: Равнозначными указанным обозначениям И и Л являются 1, что соответствует истине и 0 - высказывание ложно.

 

Понятно, что истинные и ложные высказывания образуют соответствующие множества. С помощью простых высказываний можно составлять более сложные, соединяя простые высказывания союзами “и”, “или”.

Таким образом, операции с высказываниями можно описывать с помощью некоторого математического аппарата.

 

Вводятся следующие логические операции (связки) над высказываниями

 

1) Отрицание. Отрицанием высказывания Р называется высказывание, которое истинно только тогда, когда высказывание Р ложно.

Обозначается Р или .

 

Соответствие между высказываниями определяется таблицами истинности. В нашем случае эта таблица имеет вид:

 

P	Р
И	Л
Л	И

 

2) Конъюнкция. Конъюнкцией двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинны оба высказывания.

Обозначается P&Q или РÙQ.

 

P	Q	P&Q
И	И	И
И	Л	Л
Л	И	Л
Л	Л	Л

3) Дизъюнкция. Дизъюнкцией двух высказываний P и Q называется высказывание, ложное тогда и только тогда, когда оба высказывания ложны.

Обозначается PÚQ.

 

P	Q	PÚQ
И	И	И
И	Л	И
Л	И	И
Л	Л	Л

 

4) Импликация. Импликацией двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда высказывание Р истинно, а Q – ложно.

Обозначается PÉQ (или РÞQ). Высказывание Р называется посылкой импликации, а высказывание Q – следствием.

 

P	Q	PÞQ
И	И	И
И	Л	Л
Л	И	И
Л	Л	И

 

5) Эквиваленция. Эквиваленцией двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинности высказываний совпадают.

Обозначается Р~Q или РÛQ.

 

P	Q	P~Q
И	И	И
И	Л	Л
Л	И	Л
Л	Л	И

 

С помощью этих основных таблиц истинности можно составлять таблицы истинности сложных формул.

 

Пример. С помощью таблиц истинности проверить, являются ли эквивалентными формулы j и y.

Составим таблицы истинности для каждой формулы:

 

p	r		(pÙr)
И	И	Л	И	И
И	Л	Л	Л	И
Л	И	И	Л	Л
Л	Л	И	Л	Л

 

p	r
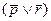
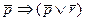
И	И	Л	Л	Л	И
И	Л	Л	И	И	И
Л	И	И	Л	И	И
Л	Л	И	И	И	И

 

Данные формулы не являются эквивалентными.

 

Пример. С помощью таблиц истинности проверить, являются ли эквивалентными формулы j и y.

 

Составим таблицы истинности для заданных формул.

 

p	q	r	pÛq	(pÛq)Úr
И	И	И	И	И
И	И	Л	И	И
И	Л	И	Л	И
И	Л	Л	Л	Л
Л	И	И	Л	И
Л	И	Л	Л	Л
Л	Л	И	И	И
Л	Л	Л	И	И

 

 

p	q	r	pÞq	qÞp	(pÞq)Ú(qÞp)	(pÞq)Ú(qÞp)Úr
И	И	И	И	И	И	И
И	И	Л	И	И	И	И
И	Л	И	Л	И	И	И
И	Л	Л	Л	И	И	И
Л	И	И	И	Л	И	И
Л	И	Л	И	Л	И	И
Л	Л	И	И	И	И	И
Л	Л	Л	И	И	И	И

 

Из составленных таблиц видно, что данные формулы не равносильны.

 

 

Основные равносильности.

 

Для любых формул А, В и С справедливы следующие равносильности:

 

A & B º B & A; A & A º A; A & (B & C) º (A & B) & C;

 

A Ú B º B Ú A; A Ú A º A; A Ú (B Ú C) º (A Ú B) Ú C;

 

A Ú (B & C) º (A Ú B) & (A Ú C); A & (B Ú C) º (A & B) Ú (A & C);

 

A & (A Ú B) º A; A Ú (A & B) º A; ØØA º A; Ø(A & B) º ØA Ú ØB;

 

A º (A & B) Ú (A & ØB); A º (A Ú B) & (A Ú ØB);

 

Булевы функции.

 

Определение. Булевой функцией f(X₁, X₂, …, X_n) называется произвольная n – местная функция, аргументы и значения которой принадлежат множеству {0, 1}.

 

Вообще говоря, между логическими высказываниями, логическими связками и булевыми функциями просматривается явная аналогия. Если логические функции могут принимать значения истинно или ложно, то для булевой функции аналогами этих значений будут значения 0 или 1.

Для булевых функций также можно составить таблицы значений, соответствующим основным логическим операциям.

 

X1	X2	ØX1	X1&X2	X1ÚX2	X1ÞX2	X1ÛX2

 

 

Исчисление предикатов.

 

Определение. Предикатом P(x₁, x₂, …, x_n) называется функция, переменные которой принимают значения из некоторого множества М, а сама функция принимает два значения: И (истина) и Л (ложь), т.е.

Предикат от п аргументов называется п – местным предикатом. Высказывания считаются нуль – местными предикатами.

Над предикатами можно производить обычные логические операции, в результате которых получаются новые предикаты.

 

Кроме обычных логических операций к предикатам применяются также специальные операции, называемые кванторами.

Кванторы бывают двух видов:

 

1) Квантор общности. Обозначается (" х) Р(х). Квантором общности называется высказывание истинное, когда Р(х) истинно для каждого элемента х из множества М, и ложное – в противном случае.

 

2) Квантор существования. Обозначается ($ х) Р(х). Квантором существования называется высказывание, истинное, когда существует элемент из множества М, для которого Р(х) истинно, и ложное в противном случае.

 

Операцию связывания квантором можно применять и к предикатам от большего числа переменных.

 

Для формул логики предикатов сохраняется справедливость всех правил равносильных преобразований логики высказываний. Кроме того, справедливы следующие свойства:

 

1) Перенос квантора через отрицание.

Ø(" x) A (x) º ($ x)Ø A (x); Ø($ x) A (x) º (" x)Ø A (x);