Критерий согласия Пирсона χ2 – один из основных, который можно представить как сумму отношений квадратов расхождений между теоретическими (fТ) и эмпирическими (f) частотами к теоретическим частотам:

k–число групп, на которые разбито эмпирическое распределение,
fi–наблюдаемая частота признака в i-й группе,
fT–теоретическая частота.
Для распределения χ2 составлены таблицы, где указано критическое значение критерия согласия χ2 для выбранного уровня значимости α и степеней свободы df (или ν).
Уровень значимости α – вероятность ошибочного отклонения выдвинутой гипотезы, т.е. вероятность того, что будет отвергнута правильная гипотеза. Р — статистическая достоверность принятия верной гипотезы. В статистике чаще всего пользуются тремя уровнями значимости:
α=0,10, тогда Р=0,90 (в 10 случаях из 100)
α=0,05, тогда Р=0,95 (в 5 случаях из 100)
α=0,01, тогда Р=0,99 (в 1 случае из 100) может быть отвергнута правильная гипотеза
Число степеней свободы df определяется как число групп в ряду распределения минус число связей: df = k –z. Под числом связей понимается число показателей эмпирического ряда, использованных при вычислении теоретических частот, т.е. показателей, связывающих эмпирические и теоретические частоты. Например, при выравнивании по кривой нормального распределения имеется три связи. Поэтому при выравнивании по кривой нормального распределения число степеней свободы определяется как df =k–3. Для оценки существенности, расчетное значение сравнивается с табличным χ2табл
При полном совпадении теоретического и эмпирического распределений χ2=0, в противном случае χ2>0. Если χ2расч> χ2табл, то при заданном уровне значимости и числе степеней свободы гипотезу о несущественности (случайности) расхождений отклоняем. В случае, если χ2расч< χ2табл то гипотезу принимаем и с вероятностью Р=(1-α) можно утверждать, что расхождение между теоретическими и эмпирическими частотами случайно. Следовательно, есть основания утверждать, что эмпирическое распределение подчиняется нормальному распределению. Критерий согласия Пирсона используется, если объем совокупности достаточно велик (N>50), при этом, частота каждой группы должна быть не менее 5.
15. Группировка, все виды средних и дисперсий при однофакторной группировке, теорема о сложении дисперсий. Задача о влиянии группировочного признака (фактора) и ее решение (критерий Фишера).
Виды дисперсий
В зависимости от того, как представлены статистические данные (единая совокупность или несколько совокупностей), различают следующие виды дисперсии: групповая; внутригрупповая; межгрупповая; общая.
Групповая дисперсия  измеряет вариацию признака внутри группы (выборки) и по своей сути является выборочной дисперсией для данной группы значений. Групповая дисперсия отражает изменчивость, которая возникает только за счет причин, действующих внутри группы (см. табл. 1).
измеряет вариацию признака внутри группы (выборки) и по своей сути является выборочной дисперсией для данной группы значений. Групповая дисперсия отражает изменчивость, которая возникает только за счет причин, действующих внутри группы (см. табл. 1).
Внутригрупповая дисперсия  является средней из групповых дисперсий и отражает случайную вариацию признака, которая происходит под влиянием всех прочих факторов, за исключением фактора, положенного в основание группировки.
является средней из групповых дисперсий и отражает случайную вариацию признака, которая происходит под влиянием всех прочих факторов, за исключением фактора, положенного в основание группировки.
Межгрупповая дисперсия  (дисперсия групповых средних) характеризует систематическую вариацию признака, которая обусловлена влиянием фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней.
(дисперсия групповых средних) характеризует систематическую вариацию признака, которая обусловлена влиянием фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней.
Общая дисперсия  измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, определяющих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений от общей средней. Можно доказать, что общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий.
измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, определяющих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений от общей средней. Можно доказать, что общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий.
Таблица 1. Формулы для расчета дисперсий
| Групповая средняя | Групповая дисперсия | Внутригрупповая дисперсия | Обозначения |

| 
| 
|  – частота значения – частота значения 
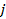 – номер группы – номер группы
 –объем группы –объем группы 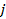
 – объем всей совокупности – объем всей совокупности
|
| Общая средняя | Межгрупповая дисперсия | Общая дисперсия | |

| 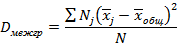
| 
|
Правило сложения дисперсий
Согласно правилу сложения дисперсий, общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий.

Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью – неизвестную. Чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группировочного признака на изучаемый признак. Поэтому в статистическом анализе широко используется эмпирический коэффициент детерминации - показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации:

При отсутствии связи эмпирический коэффициент детерминации равен нулю, а при функциональной связи – единице. Эмпирическое корреляционное отношение (см. пример) – это корень квадратный из эмпирического коэффициента детерминации:

Он показывает тесноту связи между группировочным и результативным признаками. Эмпирическое корреляционное отношение может принимать значения от 0 до 1. Если связь отсутствует, то корреляционное отношение равно нулю, т.е. все групповые средние будут равны между собой, межгрупповой вариации не будет. Значит, группировочный признак никак не влияет на образование общей вариации. Если связь функциональная, то корреляционное отношение будет равно единице. В этом случае дисперсия групповых средних равна общей дисперсии, т.е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком определяет вариацию изучаемого результативного признака. Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимости связь между признаками.
Дисперсионный анализ дает возможность установить влияние группировочного признака и влияние случайных величин на результативный признак. При этом общая дисперсия результативного признака  расчленяется на факторную
расчленяется на факторную  и остаточную (или случайную)
и остаточную (или случайную)  ; факторную дисперсию сравнивают со случайной с учетом степеней свободы. Число степеней свободы: для общей дисперсии – число значений варьирующего результативного признака без одного (n–1), для факторной дисперсии – число групп без одной (I–1), для случайной дисперсии – число значений результативного признака без числа групп (n–1). Обозначив сумму квадратов отклонений через D2, получим дисперсию на одну степень свободы:
; факторную дисперсию сравнивают со случайной с учетом степеней свободы. Число степеней свободы: для общей дисперсии – число значений варьирующего результативного признака без одного (n–1), для факторной дисперсии – число групп без одной (I–1), для случайной дисперсии – число значений результативного признака без числа групп (n–1). Обозначив сумму квадратов отклонений через D2, получим дисперсию на одну степень свободы:
– общую  ; (24)
; (24)
– факторную  ; (25)
; (25)
– случайную  . (26)
. (26)
Общая дисперсия определяется по формуле  . (27)
. (27)
Далее вся совокупность делится на однородные группы. Для каждой группы рассчитывают среднюю и дисперсию. В результате получают внутригрупповую и межгрупповую дисперсии. Общая дисперсия показывает влияние всех условий (факторов) на вариацию признака Внутригрупповая (случайная) дисперсия показывает влияние случайных, не учитываемых условий (факторов) на вариацию признака, то есть зависит от группировочного признака. Она представляет собой среднюю из частных (групповых) дисперсий ( ) и рассчитывается по формуле:
) и рассчитывается по формуле:
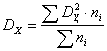 , (28)
, (28)
а частные (групповые) дисперсии рассчитываются следующим образом:
 . (29)
. (29)
Межгрупповая дисперсия характеризует вариацию признака под влиянием определяющих условий, связанных с группировочным признаком. Она представляет собой средний квадрат отклонения групповых средних от общей средней и вычисляется по формуле:
 . (30)
. (30)
Оценка достоверности влияния факторного признака на результативный производится с помощью рассчитанного значения F-критерия (критерия Фишера). Критерий Фишера есть отношение факторной и случайной дисперсий, рассчитанных на одну степень свободы:
 . (31)
. (31)
Величина рассчитанного критерия сравнивается с его табличным значением, установленным для 1- и 5-процентного уровня значимости, если значение FФАКТ < FТАБЛ.
Регрессионный анализ позволяет определить меру интенсивности направленного влияния факторов при формировании уровня производительности труда в конкретных условиях места и времени. Вначале устанавливается тип и вид функции уравнения связи. Конкретное выражение формы связи зависит от характера объективно существующей зависимости исследуемых явлений, т.е. определяется материальной природой объекта.
Количественная определенность параметров уравнения связи устанавливается чаще всего по методу наименьших квадратов. При этом находятся такие численные значения коэффициентов при факторных признаках в уравнении регрессии, при которых сумма квадратов отклонений эмпирических значений результативного показателя от аналогичных им величин, рассчитанных по теоретическому уравнению регрессии, давала бы минимальную величину.
Корреляционный анализ дает возможность измерить взаимосвязь (тесноту связи) факторного и результативного признаков. Для этого предварительно устанавливается для каждой группы центр интервала по размеру производительности труда, а затем рассчитывается коэффициент корреляции по формуле:
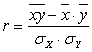 , (32)
, (32)
где  ;
;  ;
;  ;
;
 ;
;
 ;
;
X – группировочный (факторный) признак;
Y – результативный признак;
N – численность совокупности;
M – математическое ожидание;
h – среднее квадратичное отклонение.
Вычисление коэффициента корреляции является наиболее точным, если оно проводится по всему массиву не сгруппированных первичных данных.
Неравенство Крамера-Рао-Фреше. Эффективные оценки в регулярном случае. Информация Фишера и ее св-ва СКТ 224.
Информацией Фишера для плотности p(x, q) называют математическое ожидание  .
.