Распределение вероятностей называют равномерным, если на интервале которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.
Плотность вероятности равномерного распределения
Таблица №5
| Математическое ожидание | |
| Дисперсия |
Показательное распределение
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины X, которое описывается:
где λ>0.
Таблица №6
| Математическое ожидание | |
| Дисперсия |
Контрольные задания
• Оформите титульный лист к лабораторной работе, согласно требованиям СФМЭИ (ТУ). Укажите название лабораторной работы. Фамилию, Имя, группу, номер студента в журнале (см. Приложение 1).
• Создайте документ Maple. Напишите заголовок 14 кеглем, полужирно, с выравниванием по центру: «Лабораторная работа №_». Далее с выравниванием по правому краю, курсивом, 14 кеглем укажите полностью Фамилию, Имя, номер в журнале.
• Выполните задания из своего варианта, определяемого номером в журнале. Каждое задание должно быть оформлено в отдельной секции (пиктограммы 
) с заголовком «Задание №_». Завершать секцию должен развернутый ответ.
• Распечатайте лабораторную работу из под программы Maple на листах формата А4 (односторонняя печать).
При выполнении контрольных заданий студенту необходимо подставить вместо буквенных параметров индивидуальные анкетные характеристики:
- число букв в фамилии студента,
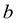- число букв в полном имени студента,
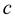- номер студента по списку в журнале.
В отчете на титульном листе необходимо обязательно указать, какие анкетные данные использовались при выполнении контрольных заданий (имя, фамилия, номер варианта).
Задания.
Задача №1.
Стрелок стреляет 9 раз по мишени. Вероятность попадания в цель при одном выстреле Написать в виде таблицы (матрицы) закон распределения случайной величины X – число попаданий по мишени. Проверить, что сумма всех вероятностей в таблице равна 1. Найти по формулам (1) и (2) математическое ожидание и дисперсию. Подтвердить полученные результаты по формулам из таблицы №1. Найти среднее квадратическое отклонение. Найти вероятность того, что стрелок попадет не менее 5 раз по мишени. Указать наивероятнейшее число попаданий.
Задача №2.
Из орудия производится стрельба до первого попадания. Вероятность попадания в цель X – дискретная случайная величина числа испытаний. Составить таблицу (матрицу) распределения для X=1,2,…10. Найти по формулам (1) и (2) математическое ожидание и дисперсию. Подтвердить полученные результаты по формулам из таблицы №2. Найти среднее квадратическое отклонение. Сколько раз надо сделать выстрелов, чтобы с вероятностью 0,999 попасть по мишени?
Задача №3.
Пусть в группе 40 студентов из них a+b отличники. Из группы случайно отбирают с+a студентов для прохождения тестирования (каждый студент может быть отобран с одинаковой вероятностью). Обозначим через Х случайную величину – m отличников среди отобранных. Найти по формулам (1) и (2) математическое ожидание и дисперсию. Подтвердить полученные результаты по формулам из таблицы №3. Найти среднее квадратическое отклонение. Найти наивероятнейшее число отличников, попавших на тестирование.
Задача №4
Валики, изготовляемые на конвейере фабрики, считаются годными, если отклонение диаметра валика от проектного размера не превышает a (мм). Случайные отклонения диаметра валиков подчиняется нормальному закону со средним квадратическим отклонением мм и математическим ожиданием m=0. Сколько годных валиков изготовляет фабрика? Дать графическую интерпретации решению задачи.
Задача №5
Цена деления шкалы амперметра равна 0,1 A. Показания округляют до ближайшего целого деления. Найти вероятность того, при отсчете будет сделана ошибка превышающая А.
Задача №6
Плотность случайной величины ξ задана законом
Вычислить значение параметра A. Построить функцию распределения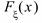 
случайной величины 
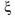. Определить случайную величину. Найти вероятности попадания случайной величины 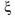в интервал (0,), (). 4) Найти числовые характеристики по определению, проверить результаты по таблице №6.