ЛАБОРАТОРНАЯ РАБОТА
«Дискретные и непрерывные случайные величины»
Оглавление
Цель...................................................................................................................................................... 1
Дискретные случайные величины........................................................................................................ 1
Непрерывные случайные величины.................................................................................................... 3
Биноминальное распределение.......................................................................................................... 5
Распределение Пуассона...................................................................................................................... 7
Геометрическое распределение.......................................................................................................... 7
Гипергеометрическое распределение................................................................................................ 9
Нормальное распределение.............................................................................................................. 11
Равномерное распределение............................................................................................................ 13
Показательное распределение.......................................................................................................... 13
Контрольные задания......................................................................................................................... 13
Цель
Целью лабораторной работы №4 является знакомство с возможностями программы Maple для расчеты распределения случайной величины по условию задачи, по нахождению ее числовых характеристик, таких как математическое ожидание, дисперсия и среднее квадратическое отклонение..
Дискретные случайные величины
Определение. Случайной величиной  называется величина, которая в результате опыта, принимает числовое значение, являющееся случайным событием этого опыта. Множество всех таких значений будем называть множеством возможных значений случайной величины
называется величина, которая в результате опыта, принимает числовое значение, являющееся случайным событием этого опыта. Множество всех таких значений будем называть множеством возможных значений случайной величины 
Определение. 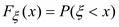 называется функцией распределения случайной величины
называется функцией распределения случайной величины 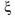 .
.
Свойства функции распределения:
1) 0<=  <=1;
<=1;
2) P{ 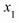 <=
<= 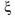 <
< 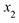 }=
}= 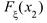 -
- 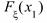 ;
;
3)  <=
<= 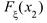 , если
, если 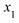 <
< 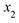 ;
;
4) 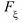 (-
(- 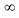 )=0,
)=0, 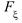 (+
(+ 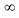 )=1.
)=1.
5) P(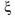 =
=  ) =
) = 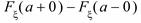
Определение. Рядом (или законом распределения) дискретной случайной величины 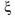 называют таблицу, в первой строке которой возможные значения
называют таблицу, в первой строке которой возможные значения 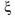 , а во второй - соответствующие вероятности
, а во второй - соответствующие вероятности 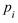 =P{
=P{ 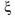 =
= 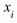 };
}; 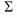
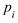 =1.
=1.
Характеристиками положения случайной величины являются математическое ожидание, мода и медиана.
Определение. Средним значением, или математическим ожиданием дискретной случайной величины  называют
называют
M[  ]=
]= 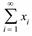
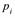 (1)
(1)
Свойства математического ожидания:
1) M[C]=C, где С - const;
2) M[C  ]=CM[
]=CM[  ];
];
3) M[ 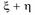 ]=M[
]=M[  ]+M[
]+M[ 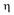 ], где
], где  и
и 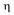 - любые случайные величины;
- любые случайные величины;
4) M[ 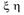 ]=M[
]=M[  ] M[
] M[ 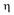 ], если
], если  и
и 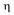 - независимые случайные величины.
- независимые случайные величины.
Случайные величины  и
и 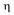 называются независимыми, если для любых x и y имеет место равенство F(x,y) =
называются независимыми, если для любых x и y имеет место равенство F(x,y) = 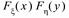 ,т.е. P({
,т.е. P({  <x,
<x, 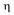 <y})=P({
<y})=P({  <x})P({
<x})P({ 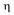 <y}).
<y}).
Модой ( ) дискретной случайной величины называется ее наиболее вероятное значение.
) дискретной случайной величины называется ее наиболее вероятное значение.
Начальные и центральные моменты k-го порядка случайной величины  определяются соответственно формулами:
определяются соответственно формулами:
 =M[
=M[  ] и
] и 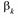 =M[
=M[ 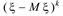 ].
].
Если  дискретная случайная величина, то
дискретная случайная величина, то 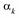 =
= 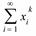
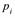 ,
, 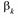 =
= 
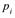 .
.
Первый начальный момент  является математическим ожиданием случайной величины
является математическим ожиданием случайной величины 
Второй центральный момент 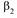 является дисперсией случайной величины
является дисперсией случайной величины  :
:
D[  ]=M[
]=M[ 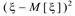 ]=
]= 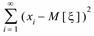
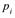 (2)
(2)
Для вычислений удобна следующая формула:
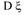 =M[
=M[ 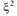 ]-
]- 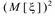 .
.
Свойства дисперсии:
1) D[C]=0, где C-const;
2) D[C  ]=
]=  D[
D[  ];
];
3) если  и
и 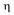 - независимые случайные величины, то D[
- независимые случайные величины, то D[  +
+ 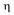 ]=D[
]=D[  ]+D[
]+D[ 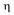 ].
].
Непрерывные случайные величины
Пусть 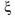 - непрерывная случайная величина и ее функция распределения
- непрерывная случайная величина и ее функция распределения 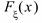 непрерывна на множестве действительных чисел.
непрерывна на множестве действительных чисел.
Определение. Плотностью вероятности назовем функцию  =
= 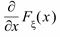
Свойства плотности вероятности:
1) 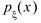 >=0;
>=0;
2) 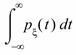 =1;
=1;
3)  =
= 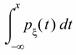
4) P{ 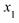 <
< 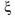 <
< 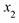 }=
}= 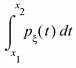
Непрерывная случайная величина задается либо функцией распределения 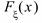 , либо плотностью вероятности
, либо плотностью вероятности 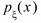 . Заметим, что функцию
. Заметим, что функцию 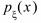 называют еще плотностью распределения случайной величины
называют еще плотностью распределения случайной величины 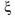 .
.
Определение. Средним значением, или математическим ожиданием непрерывной случайной величины  называют число
называют число
M[  ]=
]= 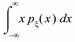 , причем предполагается, что интеграл сходятся абсолютно.
, причем предполагается, что интеграл сходятся абсолютно.
Определение. Дисперсией случайной величины  называется число
называется число
D[  ]=M[
]=M[ 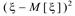 ]
]
Для непрерывной случайной величины дисперсию можно найти по формуле
D[  ]=
]=  , причем предполагается, что интеграл сходятся абсолютно.
, причем предполагается, что интеграл сходятся абсолютно.
Начальные и центральные моменты k-го порядка случайной величины  определяются соответственно формулами:
определяются соответственно формулами:
 =M[
=M[ 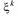 ] и
] и 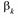 =M[
=M[ 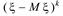 ].
].
Если  непрерывная случайная величина, то
непрерывная случайная величина, то
 =
= 
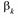 =
= 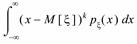
Первый начальный момент  является математическим ожиданием случайной величины
является математическим ожиданием случайной величины 
Второй центральный момент 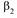 является дисперсией случайной величины
является дисперсией случайной величины  :
:
Заметим, что размерность величин 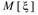 и
и  совпадает с размерностью самой случайной величины
совпадает с размерностью самой случайной величины  , а размерность
, а размерность 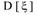 равна квадрату размерности
равна квадрату размерности  .
.