Определение. Квадратная матрица Р порядка m называется подобной матрице А, если она представлена в виде
,
где S - невыродженная квадратная матрица порядка m.
ТЕОРЕМА. Характеристический определитель исходной и подобной матрицы совпадают.
Доказательство.
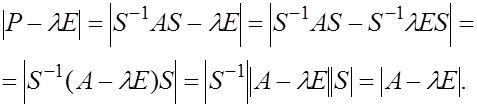
Идея метода Данилевского состоит в том, что матрица А подобным преобразованиям приводится, к так называемой нормальной форме Фробениуса
.
Характеристическое уравнение для матрицы Р имеет простой вид
т.е. коэффициенты при степенях 
характеристического полинома непосредственно выражаются через элементы первой строки матрицы Р.
Приведение матрицы А к нормальной форме Фробениуса Р осуществляется последовательно построкам, начиная с последеней строки.
Приведем матрицу А
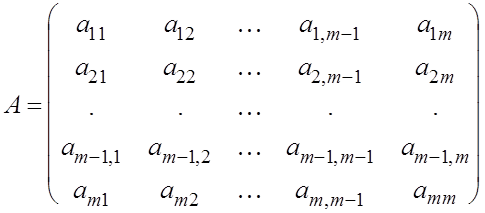
подобным преобразование к виду
Пусть 
Можн проверить,что такой вид имеет матрица 
, которая равна
где
Слудующий шаг - приведение матрицы 
подобным преобразованием к виду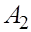 
, где и вторая снизу строка имеет единицу в 
-ом столбце, а все остальные элементы строки равны нулю:
Если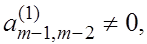 
то можно проверить, что такой вид имеет матрица :
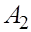где 
Таким образом
Далее процедура аналогичная, если на кождом шаге в очередной строке, на месте которого подобным преобразованием нужно получить единицу, не равную нулю.
В этом случае (будем называт его регулярным) нормальная формула Фробениуса будет получена за (m -1) шагов и будет иметь вид
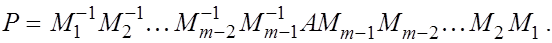
Рассмотрим нерегулярный случай, когда матрица, полученная в результате подобных преобразований приведена уже к виду
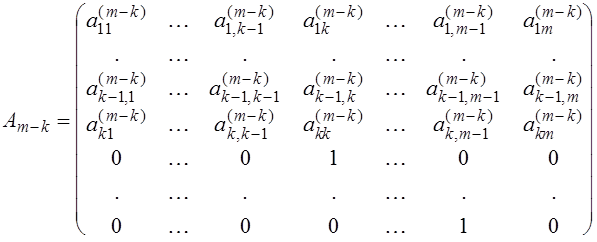и элемент 
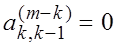. Таким образом обычная процедура метода Данилевского не подходит из-за необходимости деления на ноль.
В этой ситуации возможно два случая. В первом случае к-й
строке левее элемента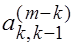 
есть элемент 
Тогда домножая матрицу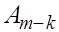 
слева и справа на элементарную матрицу перестановок 
, получаем матрицу
,
у которой по сравнению с матрицей 
переставлены l -я и (k-1)- я строка l- й и (k-1)- й стодбец. В результате на необходимом нам месте оказывается ненулевой элемент 
, уже преобразованная часть матрицы не меняется, можно применять обычный шаг метода Данилевского к матрице 
. Она подбна матрице (и, следовательно, исходной матрице А), т.к. елементарная матрица перестановок совпадает со своей обратной, т.е. 
Рассмотрим второй нерегулярный случай, когда в матрице ýлемент 
и все элементы этой строки, которые тоже находятся левее его, тоже равны нулю. В этом случае характеристический определитель матрицы можно представить в виде
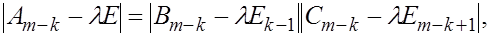
где 
і 
- единичные матрицы соответствующей размерности, а квадратные матрицы 
и 
имееют вид:
Обративм внимание на то, что матрица уже нормальную форму Фробениуса, и поэтому сомножитель 
просто развертывается в виде многочлена с коэффциентами, равными элементам первой строки.
Сомножитель 
, åñòü характеристический определитель матрицы . Для развертывания можн опять применять метод Данилевского, приводя матрицу 
подобными преобразованиями к нормальной форме Фробениуса.
Предположим теперь, что матрица А подобным преобразованиям
уже приведена к нормальной форме Фробениуса. Решая характеристическое уравнение
,
находим одним из известных методов его корни 
которые являются собственными значениями матрицы Р и исходной матрицы А.
Теперь стоит задача отыскать собственные векторы, соответствующие этим собственным значениям, т.е. векторы 
такие, что
Решим ее следующим образом: найдем собственные векторы матрицы Р, а затем по определенному соотношению я пересчитаем собственные векторы матрицы А. Это соотношение дает следующая теорема.
ТЕОРЕМА. Пусть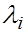 
є есть собственное значение, а 
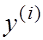есть соответствующий собственный вектор матрицы Р, которая подобна матрице А, т.е.
Тогда 
есть собственный вектор матрицы А, соответствующий собственному значению 
Доказательство. Тривиально следует из того, что
Домножая левую и правую часть этого равенства слева на S,
имеем
А это и означает, что 
-собственный вектор матрицы А,
отвечающий собственному значению
Íàéäåì ñîáñòâåííûé вектор матрицы Р, которая имеет нормальную форму Фробениуса и подобна матрице А. Записывая 
в развернутой форме, имеем
или
В этой системе одна из переменных может быть сделана свободной и ей может быть придано произвольное значение. В качестве таковой возьмем 
и положим 
Тогда последовательно находим
,
т.е. искомый собственный вектор матрицы Р имеет вид
.
Если процесс приведения матрицы А к форме Р был регулярным, то
 ñîîòâåòñòâèè ñ òåîðåìîé ñîáñòâåííûì âåêòîðîì ìàòðèöû А для собственного значения 
будет вектор
Таким образом, задача вычисления собственных векторов матрицы А решена.
ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ.
Пусть имеется функция 
которую необходимо продифференцировать несколько раз и найти эту производную в некоторой точке.
Если задан явный вид функции, то выражение для производной часто оказывается достаточно сложным и желательно его заменить более простым. Если же функция задана только в некоторых точках (таблично), то получить явный вид ее производных ввобще невозможно. В этих ситуациях возникает необходимость приближенного (численного) дифференцирования.
Простейшая идея численного дифференцирования состоит в том, что функция заменяется интерполяционным многочленом (Лагранжа, Ньютона) и производная функции приближенного заменяется соответствующей производной интерполяционного многочлена
Рассмотрим простейшие формулы численного дифференцирования, которые получаются указанным способом.
Будем предполагать, что функция задана в равностоящих узлах
Ее значения и значения производных в узлах будем обозначать
Пусть функция задана в двух точках 
и 
ее значения 
Посстроим интерполяционный многочлен первой степени
Производная 
равна
Производную функцию 
в точке 
приближенно заменяем производной интерполяционного многочлена
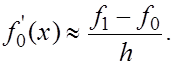(1)
Величина 
называется первой разностной производной.
Пусть 
задана в трех точках 
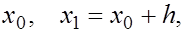
Интерполяционный многочлен Ньютона второй степени имеет вид
Берем производную
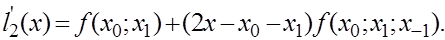
В точке она равна
Получаем приближенную формулу
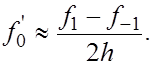(2)
Величина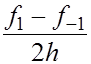 
называется центральной разностной производной.
Наконец, если взять вторую производную
получаем приближенную формулу.
(3)
Величина 
называется второй разностной производной.
Формулы (1)-(3) называются формулами численного дифференцирования.
Предполагая функцию 
достаточное число раз непрерывно дифференцируемой, получим погрешности приближенных формул (1)-(3).
В дальнейшем нам понадобится следующая лемма.
Лемма 1. Пусть 
произвольные точки, 
Тогда существует такая точка 
что
Доказательство. Очевидно неравенство
По теореме Больцано-Коши о промежуточных значениях непрерывной функции на замкнутом отрезке она принимает все значения между 
и 
Значит существует такая точка 
что выполняет указанное в лемме равенство.
Погрешности формул численного дифференцирования дает следующая лемма.
Лемма 2.
1.Предположим, что 
Тогда существует такая точка 
, что
(4)
2. Если 
то существует такая точка 
, что
(5)
3. Когда 
то существует такая, что
(6) Доказательство. По формуле Тейлора
откуда следует (4).
Если 
то по формуле Тейлора
(7)
где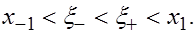 
Подставим (7) в 
Получаем
Заменяя в соответствии с леммою 1
получаем
Откуда и следует (6).
Равенство (5) доказывается аналогично (доказательство провести самостоятельно).
Формулы (4)-(6) называются формулами численного дифференцирования с остаточными членами.
Погрешности формул (1)-(3) оцениваются с помощью следующих неравенств, которые вытекают из соотношений (4)-(6):
Говорят, что погрешность формулы (1) имеет первый порядок относительно 
(или порядка 
), а погрешность формул (2) и (3) имеет второй порядок относительно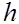 
(или порядка 
). Также говорят, что формула численного дифференцирования (1) первого порядка точности (относительно ), а формулы (2) и (3) имеют второй порядок точности.
Указанным способом можно получать формулы численного дифференцирования для более старших производных и для большего количества узлов интерполирования.
Выбор оптимального шага. Допустим, что граница абсолютной погрешности при вычислении функции 
в каждой точке удовлетворяет неравенству
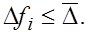(8)
Пусть в некоторой окрестности точки 
производные, через которые выражаются остаточные члены в формулах (5), (6), непрерывны и удовлетворяют неравенствам
(9)
где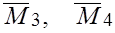 
- некоторые числа. Тогда полная погрешность формул (2), (3) (без учета погрешностей округления) в соответствии с (5), (6), (8), (9)не превосходит соответственно величин 
Минимизация по 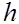этих величин приводит к следующим значениям :
(12)
при этом
(13)
Если при выбранном для какой-либо из формул (2), (3) значении отрезок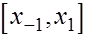 
не выходит за пределы окрестности точки 
, в которой выполняется соответствующее неравенство (9), то найденное 
есть оптимальным и полная погрешность численного дифференцирования оценивается соответствующей величиной (13).