КАЗАНСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. А.Н.ТУПОЛЕВА-КАИ
ИСПЫТАНИЯ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ
ЛАБОРАТОРНЫХ РАБОТ
Казань 2016
Составители: доцент И.А. Горбунов, проф. Ф.А. Карамов
УДК
Методические указания к выполнению лабораторных работ/Казан. нац. исслед. техн. ун-т; Сост. доцент И.А. Горбунов, проф. Карамов Ф.А., Казань, 2016 г./.
Пособие предназначено для проведения лабораторных работ с использованием методов математической статистики:
1. ОЦЕНКА РЕЗУЛЬТАТОВ ИСПЫТАНИЙ
2. ИСКЛЮЧЕНИЕ ГРУБЫХ ОШИБОК
3. ОЦЕНКА ВИДА РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
4. 4 ИСПЫТАНИЯ НА НАДЁЖНОСТЬ#
Табл. __. Ил. __. Библиограф.: __ назв.
ОЦЕНКА РЕЗУЛЬТАТОВ ИСПЫТАНИЙ
1. Точечные и интервальные оценки
Результат испытаний может быть дискретной или непрерывной случайной величиной. Так, количество дефектных изделий в выборке - дискретная случайная величина, поскольку это может быть только целое число.
Непрерывная случайная величина может принимать любое значение в некотором конечном или бесконечном интервале (например, разрывная длина бумаги). При испытаниях часто получают выборку значений непрерывной случайной величины с некоторым распределением вероятности получения того или иного значения. Наиболее часто встречается нормальное распределение. Точнее, реальные распределения в большинстве случаев достаточно близки к нормальному.
Основные параметры нормального распределения – математическое ожидание М случайной величины и её генеральное среднеквадратическое отклонение (СКО) σ (или генеральная дисперсия σ2). Математическое ожидание – это центр группировки результатов испытаний, при отсутствии систематических погрешностей соответствует количественной характеристике объекта испытаний. Дисперсия (или СКО) – мера рассеяния результатов испытаний. Найти их значения абсолютно точно невозможно. Однако при объёме выборки n не менее 25…30 обычно считают, что точечные оценки параметров нормального распределения с приемлемой точностью равны параметрам. Кроме того, можно достаточно точно рассчитать генеральную дисперсию при проведении серий испытаний, в которых генеральная дисперсия не меняется (вычисление дисперсии по текущим измерениям), например, при приёмо-сдаточных испытаниях.
Применяется также мера рассеяния, называемая коэффициентом вариации. Генеральный коэффициент вариации
γ=σ/M; (1.1)
Выборочный коэффициент вариации
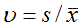(1.2)
Точечной оценкой математического ожидания М является среднее значение выборки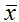 
(В Excel функция СРЗНАЧ):
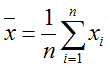
Точечной оценкой генеральной дисперсии является выборочная несмещенная дисперсия (функция ДИСП):
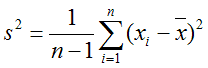
По текущим измерениям дисперсия может быть вычислена по формуле
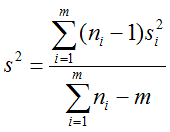
Здесь ni – объем испытаний (объём выборки) в каждой серии, si2 – дисперсии в соответствующих сериях, m – количество серий.
Оценка генерального СКО - выборочное СКО (функция СТАНДОТКЛОН):
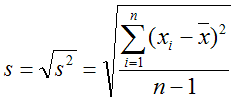
Точечные оценки малоинформативны, поскольку являются случайными величинами и могут значительно отличаться от оцениваемо-го параметра. Для повышения информативности используют интер-вальные оценки (рассчитывают доверительные интервалы).
При достаточно точно известной генеральной дисперсии σ2) доверительный интервал для математического ожидания определяют из соотношения
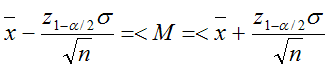(1.3)
или
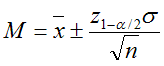
Здесь уровень значимости α=1-Р (Р -доверительная вероятность), z1-α/2 – квантиль стандартного нормального распределения (функция НОРМСТОБР), n – объём испытаний (объём выборки).
Если генеральная дисперсия неизвестна, доверительный интервал для математического ожидания определяют из соотношения
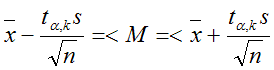
Здесь tα;k – коэффициент Стьюдента (СТЬЮДРАСПОБР), k=n-1 – число степеней свободы. Доверительный интервал для дисперсии определяют из соотношения:
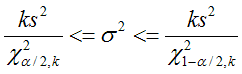
Здесь χ2 - критерий распределения хи-квадрат (функция ХИ2ОБР), k=n-1 – число степеней свободы.
Извлекая из всех частей неравенства квадратный корень, можно получить интервальную оценку СКО.
Пример 1.1. Проведены испытания на разрыв образцов дюралюминиевого профиля. Полученные значения предела прочности образцов (МПа) приведены в табл. 1.1.
Таблица 1.1.
Найти точечные и интервальные оценки параметров распределения предела прочности при доверительной вероятности 0,95.
Фрагмент выполнения примера 1.1 показан на рис.1.1.
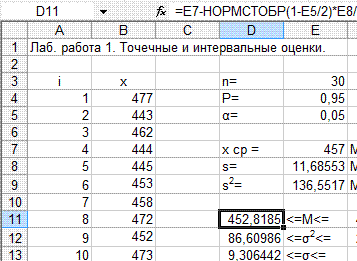
Рис. 1.1. Фрагмент расчёта для примера 1.1.
В ячейки В4:В33 вводим значения предела прочности, в ячейки А4:А33 номера соответствующих данных. В ячейке Е3 рассчитываем объём испытаний (объём выборки) функцией СЧЁТ. При этом в диалоговом окне функции СЧЁТ в строке Значение 1 вводим интервал от В4 примерно до В1000, не до В33. Это необходимо для того, чтобы электронная таблица была пересчитываема, т.е. при последующем введении других данных в другом количестве (большем или меньшем) все расчётные значения автоматически пересчитывались бы для этих новых данных. Так следует поступать и при использовании других функций.
В ячейку Е4 вводим значение доверительной вероятности. В ячейке Е5 рассчитываем уровень значимости (но не вводим в виде числа, чтобы при другой доверительной вероятности таблица автоматически пересчитывалась).
В ячейках Е7, Е8 и Е9 соответственно рассчитываем среднее значение предела прочности, его СКО и дисперсию по соответствующим статистическим формулам (поставьте размерности). В ячейках D11:D13 и F11:F13 рассчитываем соответственно нижние и верхние границы доверительных интервалов для математического ожидания, дисперсии и СКО. При этом, учитывая, что объём испытаний достаточно велик, т.е. σ примерно равно s, границы доверительного интервала для математического ожидания рассчитываем по формуле (1.3). При получении значений z и χ2 в диалоговых окнах функций НОРМСТОБР и ХИ2ОБР значения вероятностей следует получать расчётом со ссылками на ячейку со значением α, а не вводить в виде чисел, чтобы таблица была пересчитываемой. (Внимание! Адреса ячеек вводить в формулы и строки диалоговых окон следует путём указания мышью на эти ячейки., но не вводом с клавиатуры, который замедляет работу и увеличивает вероятность ошибок).
Примечания:
1. Величину доверительного интервала, в виде возможного при данном уровне значимости отклонения от среднего выборки, можно вычислить также при помощи статистической функции ДОВЕРИТ.
2. Чтобы ввести в ячейке часть текста в виде верхнего или нижнего индекса, следует в строке формул выделить необходимую часть текста, затем задать для неё верхний индекс командой Формат – Ячейки и отметкой в диалоговом окне Верхний индекс.
Задание.
1. Выполнить расчёты в соответствии с примером 1.1. Как изменяются доверительные интервалы (увеличиваются или уменьшаются) при уменьшении доверительной вероятности?
2. Найти точечные и интервальные оценки математического ожидания, дисперсии и СКО некоторой характеристики (табл. 1.2), полученной по результатам испытаний.
3. По результатам испытаний выборок из четырёх партий нанопленочных образцов получены значения разрывной длины этих образцов, представленные в табл. 1.3. Определить дисперсию по результатам испытаний всех партий (по текущим измерениям), учитывая, что генеральная дисперсия в разных партиях не меняется. Для партии 4 определить доверительный интервал для математического ожидания, используя рассчитанную дисперсию как генеральную, при доверительной вероятности 0,9.
Таблица 1.2.
| Вариант | Р | Значения характеристики | |||||||||
| 0,95 | 15,9 | 18,3 | 16,5 | 17,9 | 16,3 | 18,2 | 16,9 | 17,6 | 16,0 | 16,5 | |
| 0,90 | 7,41 | 7,50 | 7,25 | 7,63 | 7,55 | 7,66 | 7,43 | 7,38 | - | - | |
| 0,99 | - | ||||||||||
| 0,98 | 53,8 | 53,1 | 54,3 | 54,6 | 56,4 | 54,6 | 56,0 | 55,3 | 55,0 | 54,4 | |
| 0,97 | - | ||||||||||
| 0,95 | 5,6 | 5,7 | 5,8 | 5,4 | 5,9 | 5,6 | 5,5 | 5,7 | 5,5 | 5,7 | |
| 0,90 | 0,55 | 0,58 | 0,57 | 0,56 | 0,54 | 0,59 | 0,56 | 0,56 | - | - | |
| 0,99 | 8,5 | 8,7 | 8,3 | 8,7 | 8,7 | 8,9 | 8,4 | 8,9 | 9,0 | 8,6 | |
| 0,98 | 7,33 | 7,31 | 7,35 | 7,28 | 7,45 | 7,25 | 7,19 | 7,42 | - | - | |
| 0,97 | 7,51 | 6,43 | 6,34 | 7,38 | 6,96 | 7,10 | 6,88 | 7,52 | 6,56 | 6,77 | |
| 0,95 | 15,9 | 18,3 | 16,5 | 17,9 | 16,3 | 18,2 | 16,9 | 17,6 | 16,0 | 16,5 | |
| 0,90 | 7,41 | 7,50 | 7,25 | 7,63 | 7,55 | 7,66 | 7,43 | 7,38 | - | - | |
| 0,99 | - | ||||||||||
| 0,98 | 53,8 | 53,1 | 54,3 | 54,6 | 56,4 | 54,6 | 56,0 | 55,3 | 55,0 | 54,4 | |
| 0,97 | - | ||||||||||
| 0,95 | 5,6 | 5,7 | 5,8 | 5,4 | 5,9 | 5,6 | 5,5 | 5,7 | 5,5 | 5,7 | |
| 0,90 | 0,55 | 0,58 | 0,57 | 0,56 | 0,54 | 0,59 | 0,56 | 0,56 | - | - | |
| 0,99 | 8,5 | 8,7 | 8,3 | 8,7 | 8,7 | 8,9 | 8,4 | 8,9 | 9,0 | 8,6 | |
| 0,98 | 7,33 | 7,31 | 7,35 | 7,28 | 7,45 | 7,25 | 7,19 | 7,42 | - | - | |
| 0,97 | 7,51 | 6,43 | 6,34 | 7,38 | 6,96 | 7,10 | 6,88 | 7,52 | 6,56 | 6,77 | |
| 0,95 | 15,9 | 18,3 | 16,5 | 17,9 | 16,3 | 18,2 | 16,9 | 17,6 | 16,0 | 16,5 | |
| 0,90 | 7,41 | 7,50 | 7,25 | 7,63 | 7,55 | 7,66 | 7,43 | 7,38 | - | - | |
| 0,99 | - | ||||||||||
| 0,98 | 53,8 | 53,1 | 54,3 | 54,6 | 56,4 | 54,6 | 56,0 | 55,3 | 55,0 | 54,4 | |
| 0,97 | - | ||||||||||
| 0,95 | 5,6 | 5,7 | 5,8 | 5,4 | 5,9 | 5,6 | 5,5 | 5,7 | 5,5 | 5,7 | |
| 0,90 | 0,55 | 0,58 | 0,57 | 0,56 | 0,54 | 0,59 | 0,56 | 0,56 | - | - | |
| 0,99 | 8,5 | 8,7 | 8,3 | 8,7 | 8,7 | 8,9 | 8,4 | 8,9 | 9,0 | 8,6 | |
| 0,98 | 7,33 | 7,31 | 7,35 | 7,28 | 7,45 | 7,25 | 7,19 | 7,42 | - | - | |
| 0,97 | 7,51 | 6,43 | 6,34 | 7,38 | 6,96 | 7,10 | 6,88 | 7,52 | 6,56 | 6,77 |
Таблица 1.3.
| Партия | Номер образца | |||||||||
| Разрывная длина, м | ||||||||||
| - | - | |||||||||
| - |
Определение объёма испытаний
Чтобы при испытаниях получить оценку характеристики объекта испытаний с требуемой точностью и достоверностью, объем испытаний (объем выборки) должен быть не меньше некоторой величины.
Если испытания проводят для оценки математического ожидания, то при нормальном распределении характеристики минимально необходимый объем испытаний можно найти из соотношения:
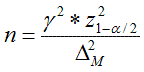(2.1)
или
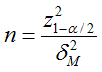(2.2)
Здесь γ - генеральный коэффициент вариации (см. формулу 1.1), z – квантиль стандартного нормального распределения, α=1-P - уровень значимости (Р - доверительная вероятность) ΔМ – максимальная относительная ошибка (допуск) при оценке математического ожидания в долях математического ожидания (или среднего значения), δМ – максимальная ошибка (допуск) при оценке математического ожидания в долях среднеквадратического отклонения.
Чаще всего генеральный коэффициент вариации неизвестен, и его заменяют выборочным коэффициентом вариации υ (ипсилон, см. формулу 1.2), полученным по предварительной информации по аналогичным объектам. Если такой информации нет, задают и уточняют в процессе эксперимента. При этом объем испытаний корректируют по формуле
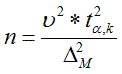(2.3)
Здесь tα,k - коэффициент Стьюдента (функция СТЬЮДРАСПОБР), k = n – 1 – число степеней свободы.
Допуск выбирают в зависимости от требуемой точности:
Низкая точность: ΔМ=γ δМ=1
Средняя точность: ΔМ=(0,4..0,5)γδМ=(0,4..0,5)
Высокая точность: ΔМ=(0,2..0,3)γδМ=(0,2..0,3)
Пример 2.1: Определить необходимый объем испытаний для оценки математического ожидания некоторой характеристики, если уровень значимости α = 0,1 и допуск ΔМ= 0,02. Данные о коэффициенте вариации отсутствуют.
Фрагмент выполнения примера 2.1 показан на рис.2.1.
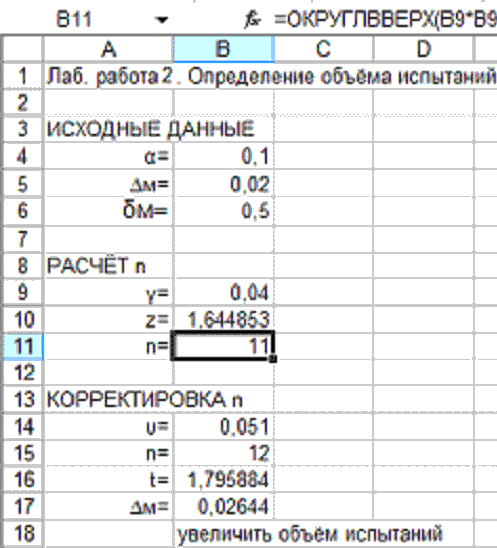
Рис. 2.1. Фрагмент расчёта для примера 2.1.
Задаемся, при средней точности, допуском ΔМ = 0,5γ, и, соответственно, δМ = 0,5. В ячейки А4, А5 и А6 вводим обозначения исходных данных α=, ΔМ= и δМ=, а в ячейки В4, В5 и В6 соответствующие значения. Приняв среднюю точность, вводим для δМ значение 0,5. Рассчитываем γ = ΔМ/δМ. Находим z1-α/2
Рассчитываем необходимый объём испытаний n по формуле (2.1). При этом, поскольку n должен быть целым числом, притом не меньшим, чем рассчитанное по (2.1) (чтобы обеспечить требуемую точность), необходимо значение, полученное по формуле (2.1), округлить до ближайшего большего целого (функция ОКРУГЛВВЕРХ). В результате расчёта получаем n = 11.
Допустим, по испытаниям 11-ти образцов выборочный коэффициент вариации υ = 0,051, что больше заданного γ. Тогда надо провести корректировку необходимого объема испытаний, т.е. увеличить его. Задаем υ = 0,051 в ячейке В14 и n = 12 в ячейке В15. Находим t0,1;11 = 1,795884 в ячейке В16. При этом в диалоговом окне функции СТЬЮДРАСПОБР в строке Вероятность делаем ссылку на значение α, а в строке Степени свободы рассчитываем k со ссылкой на заданное значение n.
После этого в ячейке В17 находим ΔМ из формулы (2.3). Если рассчитанный допуск будет больше заданного, необходимо задаваться ещё более высоким значением n, пока рассчитанное значение ΔМ не станет меньше или равно заданному. В этом случае заданное значение n принимаем как минимально необходимый объём испытаний.
Рассчитанное значение ΔМ можно сравнивать с заданным непосредственно, но для удобства это лучше сделать с помощью логической функции ЕСЛИ. Для этого в ячейку В18 вводим функцию ЕСЛИ. В диалоговом окне этой функции в строке Лог_выражение вводим необходимое логическое выражение, делая ссылки на соответствующие ячейки: B17>B5. В строке Значение_если_истина вводим фразу «Увеличить объём испытаний», в строке Значение_если_ложь вводим фразу "Объём испытаний достаточен". Если логическое выражение будет истинно, в ячейке В18 появится фраза «Увеличить объём испытаний». При этом в ячейке В15 задаём более высокое значение n, лучше всего на 1 больше. Так увеличиваем n до тех пор, пока не получим фразу "Объём испытаний достаточен".
Так, в нашем примере при n = 12 получаем ΔМ =0,02644 и вывод «Увеличить объём испытаний». Постепенно увеличивая n, получим минимально необходимый объём испытаний, и, соответственно, сколько образцов ещё надо испытать дополнительно к уже испытанным 11. Следует отметить, что после испытаний дополнительных образцов следует пересчитать выборочный коэффициент вариации и, подставив его значение в электронную таблицу, оценить, действиельно ли объём испытаний достаточен.
Если испытания проводят для оценки генерального среднеквадратичного отклонения σ (или генеральной дисперсии σ2) характеристики, то минимально необходимый объём испытаний (объём выборки) находят по формуле
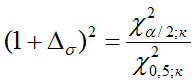(2.4)
Здесь Δσ – максимальная относительная ошибка (допуск) при оценке среднеквадратического отклонения в долях СКО; χ2α/2;k и χ20,5;k - квантили распределения Пирсона (или хи-квадрат распределения, ХИ2ОБР).
Допуск выбирают в зависимости от требований точности.
При низкой точности Δσ = 0,4...0,5
При средней точности Δσ = 0,25...0,35
При высокой точности Δσ = 0,1...0,2
Для определения минимального объёма испытаний подбирают χ2α/2;k и χ20,5;k с таким числом степеней свободы k при принятом α, чтобы выполнялось равенство (2.4). По найденному числу степеней свободы находят объем испытаний.
Пример 2.2. Определить минимально необходимый объем испытаний для оценки среднеквадратического отклонения некоторой характеристики при средней точности и доверительной вероятности 0,95.
Фрагмент выполнения примера 2.2 показан на рис.2.2.
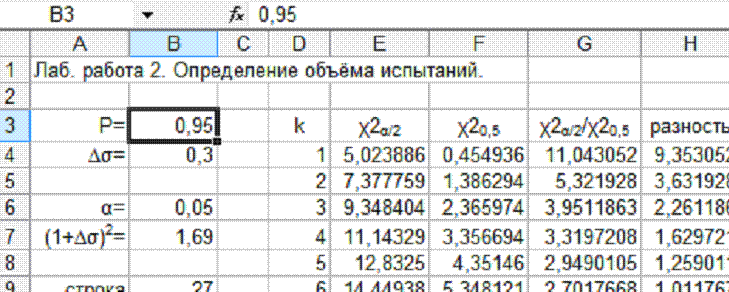
Рис. 2.2. Фрагмент расчёта для примера 2.2.
Вводим исходные данные в ячейки В3 и В4. При этом принимаем, для средней точности, Δσ = 0.3. Рассчитываем уровень значимости. Находим левую часть уравнения (2.4).
Далее возможно задать некоторое значение объёма испытаний, рассчитать правую часть уравнения (2.4), и затем подобрать минимально необходимый объём испытаний, соответствующий минимуму разности между левой и правой частями уравнения (2.4). Однако для автоматического определения необходимого объёма испытаний при вводе новых исходных данных лучше поступить так.
Вводим пять столбцов, для k, χ2α/2;k и χ20,5;k χ2α/2;k / χ20,5;k, а также для модуля (функция ABS) разности между левой и правой частями уравнения (2.4). В столбце для k вводим возможные значения степеней свободы: 1, 2, 3 и т.д., например, до 500. Для этого можно использовать команду Заполнить – Прогрессия. В остальных столбцах рассчитываем соответствующие значения, в тех же диапазонах, что и k.
Например, в столбце χ2α/2;k рассчитываем значение при k = 1 (ячейка Е4 на рис. 2.2), при этом в строках диалогового окна функции ХИ2ОБР вводим ссылку на k и формулу для расчёта α/2 со ссылкой на ячейку со значением α. Формулу из ячейки E4 копируем в диапазон Е4:E503 (этот диапазон соответствует диапазону значений k при максимальном k = 500). Однако сначала надо задать в формуле абсолютную адресацию для ячейки, в которой находится значение Α, поскольку при копировании ссылка на эту ячейку не должна меняться. Для задания абсолютной адресации перед именами строк и столбцов следует ввести символ $. Это можно сделать в строке формул вводом с клавиатуры, но более эффективно в строке формул выделить адрес нужной ячейки, нажать клавишу F4, а затем Enter. В результате, например, в ячейке Е4 должна быть получена формула =ХИ2ОБР($B$6/2;D4).
Получив значения в столбцах, следует найти номер строки, в которой находится минимальное значение модуля разности между левой и правой частями уравнения (2.4). По номеру строки можно найти число степеней свободы, а по нему – минимально необходимый объём испытаний.
Номер строки находится с использованием применяемого в Excel понятия массива. Для этого в ячейке, например, А9 вводим Строка =, в ячейке В9 вводим формулу:
=МИН(ЕСЛИ(H4:H503=МИН(H4:H503);СТРОКА(H4:H503);" "))
После этого, чтобы данная формула была формулой массива, нажимаем сочетание клавиш CTRL+SHIFT+ENTER (формула CSE), после чего формула будет заключена в фигурные скобки. Фигурные скобки указывают, что это формула массива. Следует иметь в виду, что ввод фигурных скобок с клавиатуры не даст нужного результата. Кроме того, при каждом переводе курсора в строку формулы массива необходимо заново нажимать CTRL+SHIFT+ENTER, иначе формула уже не будет восприниматься как формула массива. Эта формула массива работает так: в результате выполнения функции ЕСЛИ создается новый массив, соответствующий диапазону Н4:Н503. Если некоторая ячейка содержит минимальное значение в диапазоне (по внутренней функции МИН), массив будет содержать номер этой строки. Иначе массив содержит пустую строку (" "). Внешняя функция МИН использует полученный массив в качестве своего второго аргумента и выдаёт номер строки с минимальным значением в диапазоне Н4:Н503. Если диапазон Н4:Н503 содержит несколько одинаковых минимальных значений, формула выдаёт наименьший номер строки. Далее по номеру строки рассчитывают число степеней свободы и минимально необходимый объем испытаний для оценки среднеквадратического отклонения. В частности, для нахождения числа степеней свободы от найденного номера строки отнимают 3, поскольку значения в столбцах начинаются только с четвёртой строки.
Задание.
1. Выполнить расчёты в соответствии с примером 2.1.
2. Выполнить расчёты в соответствии с примером 2.2. Определить при этом минимально необходимый объём испытаний.
3. Рассчитать таблицу минимально необходимых объёмов испытаний для оценки математического ожидания при α, γ и ΔМ, указанных в табл. 2.1.
Таблица 2.1.
| Вариант | Уровень значимости | ΔМ | Генеральный коэффициент вариации | ||
| Минимальный | Максимальный | Шаг | |||
| 0,05 | 0,01 | 0,01 | 0,2 | 0,005 | |
| 0,1 | 0,02 | 0,02 | 0,3 | 0,005 | |
| 0,05 | 0,03 | 0,01 | 0,2 | 0,005 | |
| 0,1 | 0,04 | 0,02 | 0,3 | 0,005 | |
| 0,05 | 0,05 | 0,01 | 0,2 | 0,005 | |
| 0,1 | 0,01 | 0,02 | 0,3 | 0,005 | |
| 0,05 | 0,02 | 0,01 | 0,2 | 0,005 | |
| 0,1 | 0,03 | 0,02 | 0,3 | 0,005 | |
| 0,05 | 0,04 | 0,01 | 0,2 | 0,005 | |
| 0,1 | 0,05 | 0,02 | 0,3 | 0,005 | |
| 0,05 | 0,01 | 0,01 | 0,2 | 0,005 | |
| 0,1 | 0,02 | 0,02 | 0,3 | 0,005 | |
| 0,05 | 0,03 | 0,01 | 0,2 | 0,005 | |
| 0,1 | 0,04 | 0,02 | 0,3 | 0,005 | |
| 0,05 | 0,05 | 0,01 | 0,2 | 0,005 | |
| 0,1 | 0,01 | 0,02 | 0,3 | 0,005 | |
| 0,05 | 0,02 | 0,01 | 0,2 | 0,005 | |
| 0,1 | 0,03 | 0,02 | 0,3 | 0,005 | |
| 0,05 | 0,04 | 0,01 | 0,2 | 0,005 | |
| 0,1 | 0,05 | 0,02 | 0,3 | 0,005 | |
| 0,05 | 0,01 | 0,01 | 0,2 | 0,005 | |
| 0,1 | 0,02 | 0,02 | 0,3 | 0,005 | |
| 0,05 | 0,03 | 0,01 | 0,2 | 0,005 | |
| 0,1 | 0,04 | 0,02 | 0,3 | 0,005 | |
| 0,05 | 0,05 | 0,01 | 0,2 | 0,005 | |
| 0,1 | 0,01 | 0,02 | 0,3 | 0,005 | |
| 0,05 | 0,02 | 0,01 | 0,2 | 0,005 | |
| 0,1 | 0,03 | 0,02 | 0,3 | 0,005 | |
| 0,05 | 0,04 | 0,01 | 0,2 | 0,005 | |
| 0,1 | 0,05 | 0,02 | 0,3 | 0,005 |