Для осуществления активных операций коммерческие банки привлекают средства, проводя депозитные операции, которые являются обязательствами банка.
Задача 1. Проанализируйте структуру источников средств банка в динамике.
Таблица 3
млн.руб.
| Показатели | На начало периода | На конец периода | Отклонение (+;-) | ||
| сумма | В % к итогу | сумма | В % к итогу | ||
| Собственные источники | 1932,8 | ||||
| Уставный капитал | |||||
| Фонды | |||||
| Нераспределенная прибыль | 435,8 | 350,0 | |||
| Обязательства Кредиты, полученные от других банков | 2124,4 | 6624,1 | |||
| Остатки средств на расчетных текущих счетах предприятий и граждан | 4650,7 | 12763,4 | |||
| Средства на срочных депозитах | 382,0 | 1906,6 | |||
| Прочие | 40,9 | 68,4 | |||
| Всего источников средств | 9130,8 | 26480,3 |
За использование привлеченных средств банки выплачивают проценты, которые согласно договоренности могут выплачиваться по мере начисления или присоединяться к основной сумме долга (капитализация процентов). В зависимости от условий контрактов проценты могут начисляться на основе постоянной базы или последовательно изменяющейся (проценты на проценты). При постоянной базе начисляются простые проценты, при изменяющейся – сложные.
Основная формула наращения простых процентов имеет следующий вид:
 ,
,
где  –проценты за весь срок ссуды
–проценты за весь срок ссуды
 – первоначальная сумма долга
– первоначальная сумма долга
 – наращенная сумма или сумма в конце срока
– наращенная сумма или сумма в конце срока
 – ставка процента
– ставка процента
 – срок ссуды
– срок ссуды
При расчете простых процентов временная база K может быть равна 360 дней (12 месяцев по 30 дней), – обыкновенные проценты; 365 (366) дней (фактическая продолжительность года), - точные.
В процессе работы нередко приходится решать задачу, обратную наращению процентов, а именно, по заданной сумме S, которую требуется возвратить через определенный отрезок времени N, следует определить сумму полученной ссуды. При этом считается, что сумма S дисконтируется, а процесс начисления процентов и их изъятие называются учетом, удержанные проценты –дисконтом. Найденная в процессе исчисления величина P является новым значением суммы S. В зависимости от вида процентной ставки применяются два метода дисконтирования – математическое дисконтирование – используется ставка наращения и банковский учет – используется учетная ставка.
Математическое дисконтирование – это формальное решение следующей задачи: какую сумму ссуды требуется выдать, чтобы через определенный срок получить сумму S при начислении процентов по ставке I.
Формула
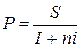 ,
,
где  – срок ссуды в годах.
– срок ссуды в годах.
Банковский учет - э то учет векселей или иного платежного обязательства, то есть приобретение банком данных бумаг до наступления срока платежа по цене, ниже стоимости, обозначенной в долговом обязательстве (с дисконтом). При наступлении срока платежа банк получает деньги и реализует дисконт.
Формула размера дисконта
 - дисконтный множитель
- дисконтный множитель
Простая учетная ставка может применяться при расчете наращенной суммы, в частности, при определении суммы, которая должна быть проставлена в векселе при заданной текущей сумме долга. В этом случае наращенная сумма определяется по формуле:

Множитель наращения 
Сложные проценты
В финансовой практике часто возникает ситуация, когда проценты не выплачиваются сразу после начисления, а присоединяются к сумме долга (капитализация процентов). В этом случае применяются сложные проценты, база для начисления которых не остается неизменной, как у простых процентов, а увеличивается по мере начисления процентов.
Для расчета наращенной суммы при условии, что проценты начисляются один раз в году, применяется следующая формула:

где i ставка наращения по сложным процентам
Проценты за этот период равны:

При условии, что проценты начисляются m раз в году, а годовая ставка равна g проценты начисляются по ставке f/m (номинальная ставка). Формула имеет следующий вид:

Использование сложных процентов осуществляется приначислении процентов на депозиты. В этом случае после очередного периода начисления, являющегося частью общего срока хранения депозита, не выплачиваются, а присоединяются к его сумме и, следовательно, на каждом последующем периоде начисления проценты будут начисляться исходя из суммы, равной первоначальной сумме депозита с начисленными за предыдущие периоды процентами.
Если проценты начисляются по сложной годовой ставке один раз в году, их сумма в конце первого года составит:
 .
.
Сумма депозита с процентами в конце первого года будет равна:
 .
.
Сумма депозита с процентами в конце второго года будет равна:
 .
.
Если срок хранения депозита n лет, то его сумма с процентами:
 .
.
Сумма начисленных процентов будет равна:
 .
.
Задача 2. Юридическое лицо открыло депозитный вклад в размере 1 млн. рублей сроком на 3 месяца в конце которого начисляются проценты из расчета 6% годовых. Определить сумму денег, которую вкладчик получит в конце указанного периода.
Задача 3. Клиент внес депозит в сумме 1000 рублей под 50% годовых. Определить сумму денег, полученных через 10 лет.
Задача 4. Депозитный вклад -1000 рублей вложен на 120 дней под 6%. Определить полученную клиентом сумму.
Задача 5. Вкладчик вложил в банк 15000 рублей, под 5% на восемь месяцев. Определить полученную им сумму.
Задача 6. Банк открыл депозит на полгода по ставке 10% годовых. Определить проценты, если сумма вклада составила 150% рублей.
Задача 7. Депозит в размере 500 тысяч рублей положен в банк на 3 года. Определить сумму начисления процентов при простой и сложной ставках процентов, равных 80% годовых.
Вопросы и задачи для индивидуальных занятий
1. Что такое проценты?
2. В чем особенности начисления процентов при использовании процентных ставок?
3. Как определяется наращенная сумма и коэффициент наращения при использовании простых процентных ставок?
4. Банк начисляет ежеквартально проценты на вклады по номинальной ставке 100% годовых. Определить сумму процентов, начисленных за 2 года на сумму 200 тысяч рублей.
5. Банк начисляет проценты на вклады по номинальной ставке сложных процентов 120% годовых. Определить доходность вкладов по эффективной годовой ставке процентов при их начислении а) по полугодиям; б) ежеквартально: в) ежемесячно.
6. На депозитный счет с начислением сложных процентов по ставке 80% годовых будут ежегодно вноситься суммы 500 тысяч рублей. Определить сумму процентов, которую банк выплатит владельцу счета, если суммы будут вноситься в конце и начале года в течение 5 лет.
Практическое занятие №3