Рациональной называется функция вида 
,
где 
и 
- многочлены степени 
и 
соответственно, 
. Поэтому интегрирование рациональных функций сводится к интегрированию многочлена и правильной рациональной дроби
, .
При этом можно считать коэффициент при 
равным единице.
Первым шагом при вычислении интеграла от функции такого вида является разложение знаменателя на множители
,
где 
- корни многочлена 
кратности 
соответственно, а трехчлены 
, 
не имеют действительных корней 
. При этом 
.
Следующим шагом является представление дроби в виде суммы простейших дробей:
.
Здесь 
- некоторые числа, которые находятся методом неопределенных коэффициентов. Заключается он в том, что правая часть последнего равенства приводится к общему знаменателю. В числителе получившегося выражения получается некоторый многочлен степени , коэффициенты которого, выраженные через искомые константы, надо приравнять к коэффициентам многочлена . Получается система 
линейного уравнения. Рассмотрим пример
.
.
Отсюда
.
Решая эту систему, получим значения 
, 
, 
, 
, 
. Поэтому
.
Есть другие методы нахождения коэффициентов разложения, которые не столь универсальны, как изложенный выше, но в в частных случаях бывают гораздо удобнее. Например, если знаменатель имеет только действительные простые (кратности один) корни, можно поступить следующим образом.
.
.
Положим поочередно 
. Получим равенства
.
Отсюда 
.
.
Если знаменатель имеет действительные корни, среди которых есть корни кратности больше единицы, то поступим так:
.
.
Положим 
, тогда 
. Теперь положим 
, получим 
. Осталось найти А. Продифференцируем предыдущее тождество:
.
Положим 
равным значению кратного корня, т.е. , тогда
.
.
Итак, разбивая правильную дробь на простейшие, мы ее интегрирование сводим к интегрированию дробей следующих видов:
1) 
; 2) 
; 3) 
; 4) 
.
Посчитаем интегралы от этих дробей:
1) 
; 2) 
;
3) 
.
Здесь надо заметить, что 
так как 
- дискриминант квадратного трехчлена 
, не имеющего действительных корней, а значит, отрицательный.
4) 
.
В последнем интеграле делается подстановка 
:
.
Вычисление такого интеграла рассмотрим в п. 6.
Еще один способ вычисления интеграла 
- использовать рекуррентное соотношение, которое сейчас установим.
.
Например, посчитаем интеграл
. Следовательно, вышеприведенный интеграл окончательно имеет вид:
.
Упражнение. Решить соответствующие задания из расчетно-графической работы.
Метод Остроградского
Пусть знаменатель несократимой дроби имеет вид
.
Метод Остроградского заключается в использовании формулы
.
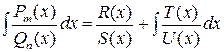В ней многочлены 
и 
имеют вид
,
соответственно и могут быть вычислены без разложения многочлена на произведение неприводимых множителей.
Действительно, является наибольшим общим делителем двух многочленов и 
, и может быть вычислен при помощи алгоритма Евклида, который излагается в курсе алгебры.
Остается вычислить многочлены 
и 
как многочлены с неопределенными коэффициентами степени на единицу ниже, чем и соответственно. Для вычисления указанных неопределенных коэффициентов следует продифференцировать формулу Остроградского, привести результат дифференцирования к общему знаменателю и сопоставить коэффициенты при одинаковых степенях х в числителях.
Метод Остроградского особенно эффективен, когда корни в основном являются кратными или когда вызывает затруднение нахождение корня .
Вычислим 
.
Имеем 
, 
.
Наибольший общий делитель этих многочленов равен
.
Поделив на «столбиком», найдем
.
и задаем как многочлены первой степени с неопределенными коэффициентами, и формула Остроградского принимает вид
Продифференцируем эту формулу:
.
Результат дифференцирования приводим к общему знаменателю, после чего сопоставляем числители. Получим
.
Сопоставляя коэффициенты при 
и 
, получим систему уравнений:
Решая эту систему, найдем 
. Таким образом формула Остроградского принимает вид:
.
Вычислим интеграл в правой части:
.
Окончательно имеем
.
Рассмотрим еще один пример.
Разложим знаменатель на множители:
.
Отсюда 
.
.
Приравнивая коэффициенты:
.
.
Упражнение. Применяя метод Остроградского найти соответствующие интегралы из расчетно-графической работы.