Ускорение при равномерном движении тела (точки) по окружности

В школьных учебниках физики для вывода формулы центро­стремительного ускорения чаще всего используют способ, основан­ный на предельном переходе. Однако ввиду отсутствия знаний у уча­щихся VIII класса о предельном переходе в курсе школьной механи­ки он является нестрогим и трудно усваивается учащимися. Поэтому наиболее продуктивно использовать следующий подход. Вначале следует обратить внимание на то обстоятельство, что при равномерном движении материальной точки по окружности вектор скорости непрерывно изменяется по направлению. Следовательно, за промежуток време­ни происходит некоторое изменение скорости 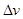. Таким образом, v ~ t. В этом случае движения возникает ускорение .

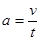Важно заметить, что здесь речь идет об ускорении в точке окружности, а значит промежуток времени берется достаточно малым. Чтобы определить направление вектора а, его модуль |а|, например, в точке А окружности (Рис. 3), ццелесообразно воспользоваться свойством двух векторов, имеющих равные модули и образу­ющих малый угол, и зависи­мостью между линейной и угловой скоростями.

Пусть за очень малый промежуток времени тело переместилось из точки А в точку В (см. Рис. 3). Тогда изменение вектора скорости 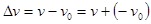. Следовательно, для определения 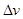достаточно к вектору 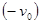прибавить вектор . Из рисунка видно, что вектор 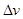, равный разности , направлен в сторону кривизны окружности в точке А. По свойству векторов модуль разности двух равных векторов, образующих малый угол , равен произведению модуля вектора на угол, т. е. . Кроме того, в этом случае вектор 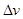должен быть перпендикулярен вектору (так как между векторами и угол мал). Вектор скорости (как и ) направлен по Касательной, а касательная перпендикулярна радиусу. Отсюда следует, что вектор 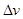должен быть направлен по радиусу окружности, и направлен к ее центру. Из формулы - следует, что вектор ускорения имеет такое же направление, что и вектор 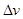(так как время – скалярная величина). Таким образом, учащиеся подводятся к выводу: вектор ускорения, возникающего при равномерном движении окружности тела или точки, всегда направлен по радиусу к центру окружности. Поэтому такое ускорение называется центростремительным.

Далее находят модуль центростремительного ускорения .

Необходимо обратить внимание учащихся еще на следующий факт. Так как | v | и R — постоянные величины, то модуль при равно­мерном движении тела по окруж­ности остается все время неиз­менным. Однако отсюда еще нельзя сделать заключение, что такое движение равноускорен­ное. Так как в процессе рав­номерного движения тела по ок­ружности вектор ускорения нап­равлен по радиусу к центру, то непрерывно изменяется его нап­равление. Таким образом, рав­номерное движение тела (точки) по окружности есть движение с переменным ускорением; оно не является равноускоренным .

При изучении движения по окружности нуждаются в конкрети­зации понятия «число оборотов в единицу времени», «линейная скорость» и особенно «центростремительное ускорение», которые для учащихся весьма абстрактны. Не ограничиваясь формальным опре­делением, полезно показать устройства с известными числами обо­ротов (лучше для начала с небольшими), например: электродвига­тель, центробежную машину с червячной передачей (число оборотов которой определяется демонстрационным тахометром), электробы­товые приборы, в первую очередь наиболее доступный из них – настольный вентилятор (число оборотов вентилятора берем из таб­лицы). После этого можно привести аналогичные данные о машинах и приборах, применяемых в технике (например, скорость вращения пропеллера самолета и вертолета). Для ребят интересно будет узнать, что винт вертолета вращается сравнительно медленно: всего в три раза быстрее, чем диск электропроигрывателя при максимальной скорости. Электро­проигрывателем, центробежной машиной и настольным вентилятором можно воспользоваться и для подсчёта линейных скоростей и цен­тростремительных ускорений конкретных точек. Например, при наращении диска со скоростью 33 об/мин центростремительное уско­рение его наиболее удаленных точек составляет около 1 м/с², что может служить своеобразным эталоном этой величины. Точка лопасти настольного вентилятора, отстоящая от оси вращения на 10 см, Движется со скоростью 12 м/с и с центростремительным ускорением 440 м/с².

Заключение

Формирование основных понятий вращательного движения, как составной части криволинейного движения, является довольно трудной для усвоения темой. Она нуждается во множестве примеров и демонстраций, вполне возможных для проведения на уроке. Полученные знания будут находить применение в последующих темах изучения физики. Ученик, свободно оперирующий понятиями вращательного движения, подготовлен к изучению динамики вращательного движения. Также знание понятий будет использоваться в теме колебаний. Следуя этапам, рекомендованным в данной работе, можно в достаточной степени закрепить у учащихся средней школы понимание рассматриваемых понятий, необходимое для дальнейшего изучения физики, формирования навыков решения задач кинематики вращательного движения, понимания использования данных понятий в быту.

Литература

1. С.У. Гончаренко «Фізика 9»

2. В. П. Орехова, А. В. Усовой «Методика преподавания физики 8-10 кл.» «Просвещение »1980 г.

3. Я.И. Перельман «Занимательная физика» Кн.2/под ред. А.В. Митрофанова; М. «Наука» 1986 г.