Важнейшими характеристиками случайных величин являются математическое ожидание и дисперсия.
Математическим ожиданием или средним значением дискретной с. в.  называется сумма произведений всевозможных значений с. в. на их вероятности:
называется сумма произведений всевозможных значений с. в. на их вероятности:
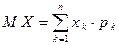 или
или 
в зависимости от того, конечнозначной или счётнозначной является данная с. в.
Математическим ожиданием непрерывной с. в.  называется интеграл
называется интеграл

при условии, что он сходится.
Свойства МХ:
1. 
2. 
3. 
4.  если
если  и
и  - независимые с. в.
- независимые с. в.
Рассеивание с. в.  характеризуется либо дисперсией, либо средним квадратическим отклонением.
характеризуется либо дисперсией, либо средним квадратическим отклонением.
Дисперсия с. в.  - это математическое ожидание квадрата отклонения с. в. от своего математического ожидания:
- это математическое ожидание квадрата отклонения с. в. от своего математического ожидания:

Свойства DX:
1. 
2. 
3. 
4.  для независимых с.в.
для независимых с.в.  и
и  .
.
Средним квадратическим отклонением с. в.  называется арифметический корень из дисперсии
называется арифметический корень из дисперсии

 Биномиальным называют закон распределения д.с.в. X – количества появлений события
Биномиальным называют закон распределения д.с.в. X – количества появлений события 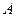 в серии
в серии  независимых повторных испытаний:
независимых повторных испытаний:






 0 1 2...
0 1 2...  ...
... 


 .
.


 ...
...  ...
... 
Здесь  - вероятность появления события
- вероятность появления события 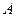 в каждом испытании, а
в каждом испытании, а  Числовые характеристики биномиального распределения:
Числовые характеристики биномиального распределения:

Говорят, что непрерывная случайная величина Х имеет экспоненциальное или показательное распределение, если плотность распределения имеет вид:

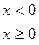 .
.
При этом
 ,
, 
 ,
,

 < 0
< 0


Пример 7.1. Пусть с.в.  - количество автомобилей, подъезжающих к АЗС в случайный момент времени
- количество автомобилей, подъезжающих к АЗС в случайный момент времени  имеет закон распределения
имеет закон распределения




 0 1 2 3 4
0 1 2 3 4


0,1 0,2 0,4 0,15 0,15
Найти 
Решение.

Составим закон распределения с.в. 
 |  |  |  |  |
0 1 4 9 16

 :
:
0,1 0,2 0,4 0,15 0,15
и найдём её математическое ожидание:


Тогда


Пример 7.2. Устройство состоит из трёх независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения с.в. X числа отказавших элементов в одном опыте.
Найти  Составить функцию распределения
Составить функцию распределения  и построить её график.
и построить её график.
Решение. С.в.  принимает следующие возможные значения:
принимает следующие возможные значения:
0 – не откажет ни один элемент;
1 – откажет один элемент из трёх;
2 – откажут два элемента;
3 – откажут все три элемента.
Поскольку отказы элементов происходят независимо один от другого, то для расчёта вероятностей числа отказов можно использовать формулу Бернулли, где 




Контроль: 0,729 + 0,243 + 0,027 + 0,001 = 1.
Запишем искомый биноминальный закон распределения:



 0 1 2 3
0 1 2 3
 Х:
Х:
0,729 0,243 0,027 0,001
(контроль: 0,729+0,243+0,027+0,001=1)
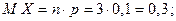

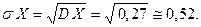
Функция распределения с.в. 
 рассчитывается таким образом:
рассчитывается таким образом:
Для 
 т. к. с.в.
т. к. с.в.  не принимает значений меньших 0.
не принимает значений меньших 0.
Далее: 

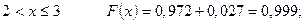

Итак, функция распределения с.в.  оказалась кусочно-постоянной, имеющей «ступенчатый» график (рис. 3)
оказалась кусочно-постоянной, имеющей «ступенчатый» график (рис. 3)
 Y
Y












 |
0 1 2 3 4 x
Рис. 3
Пример 7.3. Станок-автомат штампует детали. Вероятность того, что случайно отобранная деталь окажется бракованной, равна 0,01. Найти вероятность того, что среди 200 деталей бракованных окажется не больше трёх.
Решение. Вероятность искомого события А можно найти, применяя теорему сложения для независимых событий:
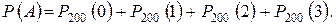
Поскольку число  велико, а вероятность появления бракованных деталей р мала, то все слагаемые, стоящие в правой части равенства, могут быть рассчитаны по формуле Пуассона:
велико, а вероятность появления бракованных деталей р мала, то все слагаемые, стоящие в правой части равенства, могут быть рассчитаны по формуле Пуассона:

В нашем случае  и, значит,
и, значит,


Таким образом, 
Пример 7.4. Время обслуживания в некоторой системе подчиняется экспоненциальному закону с интенсивностью 4 требования в час. Найти вероятность того, что время обслуживания окажется в интервале от 20 до 36 минут. Какова вероятность того, что требование будет обслужено в течение часа?
Решение. По условию, функция распределения времени обслуживания имеет вид:

Вероятность того, что время обслуживания T будет находиться в интервале 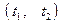 найдём по формуле
найдём по формуле
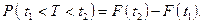
В нашем случае,  минутам
минутам  часа,
часа,  минутам = 0,6 часа. Значит,
минутам = 0,6 часа. Значит,

Аналогично,

Пример 7.5. Случайная величина Х называется равномерно распределённой на отрезке  , если плотность её распределения имеет вид:
, если плотность её распределения имеет вид:

Найти 
Решение.


Тогда,  а значит
а значит 
Пример 7.6. Дана функция распределения с.в. X:

Найти: 
Решение. По определению





Наконец,

Пример 7.7. С.в.  задана плотностью распределения
задана плотностью распределения

Найти коэффициент 
Решение. Для нахождения коэффициента  воспользуемся соотношением
воспользуемся соотношением

Имеем
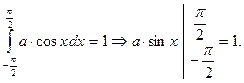

и, значит,

Тогда:

= 

Вероятность попадания с.в.  в заданный интервал находим в виде интеграла
в заданный интервал находим в виде интеграла

Задачи для самостоятельной работы
7.1. На автобазе 12 грузовиков. Вероятность выхода на линию каждого грузовика равна 0,9. Найти вероятность нормальной работы автобазы, если для этого необходимо, чтобы на линии было не менее 10 грузовиков. (Отв.: 0,889)
7.2. В цеху имеется две конвейерные линии, работающие независимо друг от друга. Вероятность того, что в случайный момент времени свободна 1-ая линия равна 0,2, что свободна 2-ая равна 0,1. Составить закон распределения с.в.  - числа свободных линий. Найти
- числа свободных линий. Найти  и
и  . (Отв.: 0,3; 0,5)
. (Отв.: 0,3; 0,5)
7.3. На аэродроме 5 взлётно-посадочных полос. Вероятность того, что в данный момент времени каждая полоса свободна, равна 0,3. Составить закон распределения с.в.  - числа свободных взлётно-посадочных полос.
- числа свободных взлётно-посадочных полос.
 |  |  |  |  |  |
 (Отв.: 0 1 2 3 4 5)
(Отв.: 0 1 2 3 4 5)
0,168 0,360 0,309 0,132 0,028 0,003
7.4. Устройство состоит из 1000 элементов, работающих независимо одно от другого. Вероятность отказа любого элемента в течение времени  равна 0,002. Найти вероятность того, что за время
равна 0,002. Найти вероятность того, что за время  откажут ровно три элемента. Найти вероятность того, что откажут не более трёх элементов.
откажут ровно три элемента. Найти вероятность того, что откажут не более трёх элементов.
(Отв.: 0,181; 0,861)
7.5. Время обслуживания требований в СМО подчиняется экспоненциальному закону с интенсивностью  требований в час. Найти вероятность того, что время обслуживания будет находиться в интервале от 6 до 24 минут. Какова вероятность того, что требование будет обслужено в течение часа? (Отв.: 0,455; 0,9975)
требований в час. Найти вероятность того, что время обслуживания будет находиться в интервале от 6 до 24 минут. Какова вероятность того, что требование будет обслужено в течение часа? (Отв.: 0,455; 0,9975)
7.6. Задана плотность распределения с.в. Х:

Найти 
(Отв.:  )
)
7.6. Дан закон распределения д.с.в.




 Х: -3 -2 1 2 4
Х: -3 -2 1 2 4
 0,3 0,2 0,1 0,3 0,1.
0,3 0,2 0,1 0,3 0,1.
Найти 
(Отв.: -0,2; 6,36; 0,6)
7.7. Функция распределения с.в.  задана
задана

Найти  (Отв.:
(Отв.: 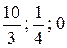 )
)
7.9. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудет не более трёх бракованных изделий. (Отв.: 0,98)
7.10 Функция распределения времени обнаружения затонувшего судна имеет вид: 
Найти среднее время поиска, необходимое для обнаружения судна. (Отв.:  ).
).
§8. Нормальное распределение
С.в.  называется нормально распределённой, если плотность вероятностей имеет вид
называется нормально распределённой, если плотность вероятностей имеет вид

График 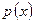 имеет форму «колокола» - симметричной кривой (рис.4), которую называют нормальной кривой или кривой Гаусса. Расчёты показывают, что
имеет форму «колокола» - симметричной кривой (рис.4), которую называют нормальной кривой или кривой Гаусса. Расчёты показывают, что
 , т.е. параметр
, т.е. параметр  - это среднее значение с.в.
- это среднее значение с.в.  , а параметр
, а параметр  -её среднее квадратическое отклонение. Поэтому, прямая
-её среднее квадратическое отклонение. Поэтому, прямая  является
является
осью симметрии графика, а  характеризует степень «крутизны» или «пологости» графика.
характеризует степень «крутизны» или «пологости» графика.
На рисунке 5 изображены графики двух нормальных распределений.

 Y
Y 
 |
 |
0 а х
Рис. 4








 у которых математическое ожидание
у которых математическое ожидание  одинаково, но у второго графика среднее квадратическое отклонение больше, чем у первого, т.е.
одинаково, но у второго графика среднее квадратическое отклонение больше, чем у первого, т.е. 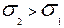 и, поэтому, график
и, поэтому, график  является более «пологим», чем
является более «пологим», чем  . Y Это означает, что с.в.
. Y Это означает, что с.в.  ,
,  плотность распределения которой
плотность распределения которой  , является более рассеянной относительно центра распределения
, является более рассеянной относительно центра распределения  (математического ожидания), чем с.в.
(математического ожидания), чем с.в.  , имеющая плотность распределения вероятностей
, имеющая плотность распределения вероятностей  . Заметим, что при любых
. Заметим, что при любых  и
и  0
0 
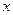 площадь под нормальной кривой Рис. 5 равна 1. Тот факт, что с.в.
площадь под нормальной кривой Рис. 5 равна 1. Тот факт, что с.в.  имеет
имеет
нормальное распределение с параметрами  и
и  коротко записывается так:
коротко записывается так:  .
.
Вероятность попадания нормально распределённой с.в.  в заданный интервал (α; β) находится по формуле
в заданный интервал (α; β) находится по формуле
 Ф
Ф  Ф
Ф  , (8.1)
, (8.1)
где Ф 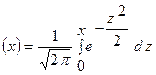 - функция Лапласа, значения которой находятся
- функция Лапласа, значения которой находятся
по таблице.
Свойства Ф  :
:
1. Ф (0) = 0;
2. Ф (х) – возрастающая функция;
3. Ф (x) 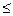 0,5 и Ф (x) = 0,5
0,5 и Ф (x) = 0,5  ;
;
4. Ф (-x) = - Ф (x).
Следующее равенство, вытекающее из (8.1), позволяет вычислить вероятность того, что отклонение нормально распределённой с.в.  от своего среднего значения не превосходит заданной величины. Если
от своего среднего значения не превосходит заданной величины. Если  , то
, то
 Ф
Ф  (8.2)
(8.2)
В частности, взяв  , получаем:
, получаем:
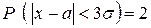 Ф(3)=0,9973.
Ф(3)=0,9973.
Таким образом, с вероятностью 0,9973, т.е. практически достоверно, можно утверждать, что абсолютная величина отклонения значений нормально распределённой с.в. от своего среднего не превышает 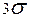 . Это утверждение называют правилом
. Это утверждение называют правилом  .
.
Пример 8.1.  . Найти
. Найти 
Решение. По формуле (8.1) имеем:
 Ф
Ф  Ф
Ф 
=Ф (2)-Ф (-2)=2Ф (2)= 
Пример 8.2. На станке изготавливается деталь. Её длина представляет с.в.  , распределённую по нормальному закону со средним значением а = 19,8 см. и
, распределённую по нормальному закону со средним значением а = 19,8 см. и
средним квадратическим отклонением  =0.2 см. Найти вероятность того, что длина детали окажется между 19,7 см. и 20,3 см.
=0.2 см. Найти вероятность того, что длина детали окажется между 19,7 см. и 20,3 см.
Решение. Вновь используем формулу (8.1):
 Ф
Ф  Ф
Ф  = Ф (2,5)+Ф (0,5) =
= Ф (2,5)+Ф (0,5) =
= 
Пример 8.3. При измерении диаметра валика микрометром случайная погрешность подчинена нормальному закону со средним отклонением 0,15 мм. Найти вероятность того, что измерение произойдёт с ошибкой, не превосходящей по абсолютной величине 0,2 мм.
Решение. Поскольку речь идёт о случайной погрешности с.в.  , то
, то  и, используя формулу (8.2), получаем:
и, используя формулу (8.2), получаем:
 Ф
Ф  2Ф (1,33) =
2Ф (1,33) = 
Случайная величина  называется нормированной, если
называется нормированной, если  и
и 
Если  - с.в., имеет
- с.в., имеет  и
и 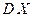 , то с ней можно связать нормированную с.в.
, то с ней можно связать нормированную с.в.  :
:

Рассмотрим с.в. 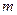 - число появлений события
- число появлений события 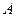 в серии
в серии  независимых повторных испытаний, в каждом из которых вероятность появления события
независимых повторных испытаний, в каждом из которых вероятность появления события 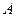 равна
равна  ,
, 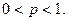 Известно, что с.в.
Известно, что с.в. 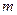 имеет биномиальное распределение с параметрами
имеет биномиальное распределение с параметрами 
Составим нормированную с.в. 

Интегральная теорема Лапласа
Если  и
и  достаточно большое число, то с.в.
достаточно большое число, то с.в.  подчиняется нормальному закону и справедливо асимптотическое1 равенство
подчиняется нормальному закону и справедливо асимптотическое1 равенство
 Ф
Ф  Ф
Ф  , где
, где  (8.3)
(8.3)
Пример 8.4. Вероятность изготовления качественной детали на данном станке равна 0,85. Найти вероятность того, что из 400 деталей качественных окажется не менее 330.
Решение. По условию: 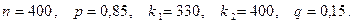
Для того чтобы воспользоваться формулой (8.3) подготовим:


Итак,
 Ф (8,4) - Ф (-1,4) = Ф (8,4) + Ф (1,4) = 0,5 + 0,4192 = 0,9192.
Ф (8,4) - Ф (-1,4) = Ф (8,4) + Ф (1,4) = 0,5 + 0,4192 = 0,9192.
Из формулы (8.3) получается ещё одно важное следствие: в серии  независимых повторных испытаний вероятность отклонения относительной частоты появления события
независимых повторных испытаний вероятность отклонения относительной частоты появления события 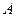 от его вероятности
от его вероятности  удовлетворяет соотношению:
удовлетворяет соотношению:
 (8.4)
(8.4)
Пример 8.5. Вероятность попадания в цель при одном выстреле равна 0,9. Найти вероятность того, что при 300 выстрелах относительная частота попадания отклонится от вероятности 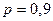 не более чем на 0,02.
не более чем на 0,02.
Решение. Воспользуемся формулой (8.4) с 
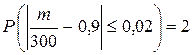 Ф
Ф  .
.
Пример 8.6. Вероятность того, что выпускаемая деталь окажется нестандартной, равна 0,05. Сколько деталей следует изготовить, чтобы с вероятностью 0,996 можно было бы утверждать, что относительная частота появления нестандартной детали отклонится от вероятности 0,05 не более чем на 0,02?
Решение. Мы вновь будем использовать формулу (8.4), но теперь искомой величиной является число испытаний  . Учитывая, что
. Учитывая, что
 мы получаем:
мы получаем:

Ф 
По условию 2Ф 
то есть Ф 
В таблице функции Ф(х), стр. 41-42 находим, что вероятности 0,498 соответствует значение аргумента, равное 2,88; поэтому
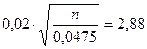
откуда 
и поскольку  должно быть целым, заключаем, что
должно быть целым, заключаем, что 
Вывод: для того, чтобы с вероятностью 0,996 быть уверенным в том, что относительная частота нестандартных деталей отклонится от вероятности 0,05 не более чем на 0,02, необходимо изготовить не менее 985 деталей.