Для того чтобы функция 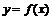 была бы дифференцируемой в точке
была бы дифференцируемой в точке 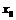 , необходимо и достаточно, чтобы она имела в этой точке конечную производную.
, необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Отметим, что при этом 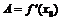 .
.
Из определения дифференцируемости непосредственно вытекает
Теорема.
Если функция дифференцируема в точке 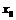 , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
Обратное утверждение неверно: достаточно рассмотреть функции 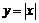 или
или 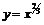 в точке
в точке 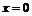 .
.
Пример 3. Пользуясь основными правилами дифференцирования и формулой для производной экспоненты, найти производные гиперболических функций.
1) 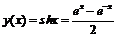
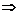
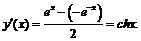
2) 
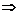
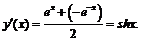
3) 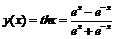
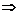

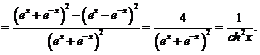
4) 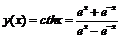
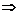
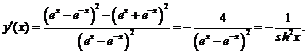
Рассмотрим ряд примеров на вычисление производных сложных функций.
Пример 4. 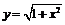 ,
, 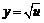 ,
,
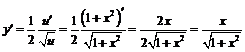 .
.
Пример 5. 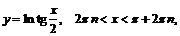
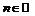 .
.
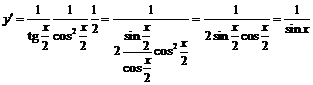 .
.
Пример 6. 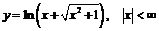 .
.
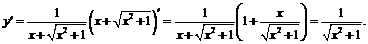
Пример 7. 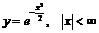 .
.
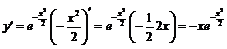 .
.
Если правило дифференцирования сложной функции применить для четной или нечетной функции, то приходим к ранее доказанным соотношениям:
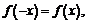
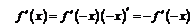 ;
;
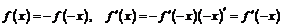 .
.
Теорема о производной обратной функции
Пусть функция 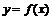 непрерывна и строго монотонна в некоторой окрестности точки
непрерывна и строго монотонна в некоторой окрестности точки 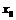 и в этой точке имеет отличную от нуля производную
и в этой точке имеет отличную от нуля производную 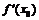 . Тогда обратная функция
. Тогда обратная функция 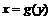 в соответствующей точке
в соответствующей точке 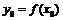 также имеет производную, равную
также имеет производную, равную 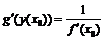 .
.
Пример 8. Найти производные обратных тригонометрических функций.
1) 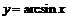 ,
, 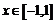 ; 2)
; 2) 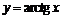 ,
, 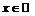 ;
;
3) 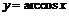 ,
, 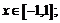 4)
4) 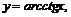
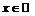 .
.
1) 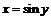 ,
, 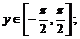

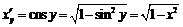
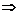
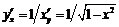 .
.
2) 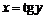 ,
, 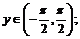

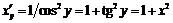
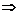
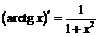 .
.
3)-4) В силу тождеств 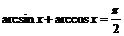 ,
,
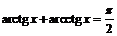
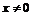 заключаем, что
заключаем, что
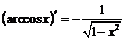 ,
, 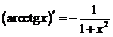 .
.
Результаты, полученные в примерах 1, 3, 8 приводят нас к таблице основных производных.
Таблица производных основных элементарных функций
Если 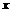 - независимая переменная, то
- независимая переменная, то
I. 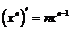 ,
, 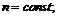
II. 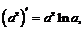
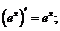
III. 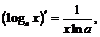
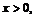
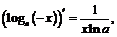
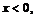
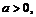
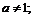
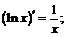
IV. 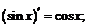 V.
V. 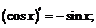
VI. 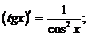 VII.
VII. 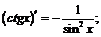
VIII. 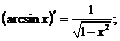 IX.
IX. 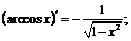
X. 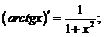 XI.
XI. 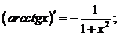
XII. 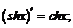 XIII.
XIII. 
XIV. 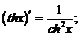 XV.
XV. 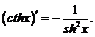
Пример 9. Найти производную функции 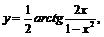
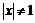 .
.
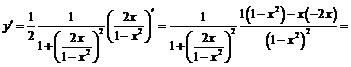
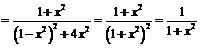 .
.
Пример 10. Найти производную функции 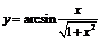 .
.
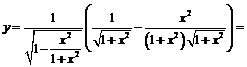
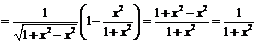 .
.
Как следствие примеров 9, 10 имеем тождества:
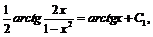
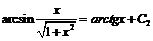 .
.
Если 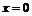 , то получим:
, то получим:  ,
, 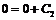 , откуда следует, что
, откуда следует, что 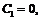
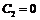 , и тождества примут вид:
, и тождества примут вид:
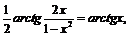
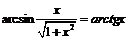 .
.
Пример 11. Найти производную функции
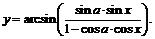
Функция определена, если 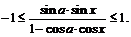 Это неравенство равносильно неравенствам:
Это неравенство равносильно неравенствам: 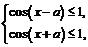 которые выполняются для
которые выполняются для 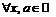 . Итак, функция определена на
. Итак, функция определена на 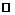 . Найдём её производную:
. Найдём её производную:
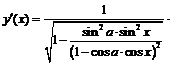
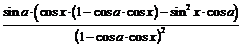 .
.
После преобразований подкоренного выражения
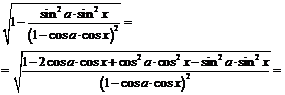
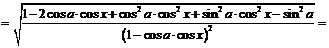
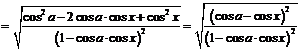 ,
,
получим:
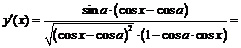
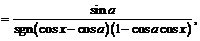
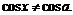
Таким образом, 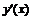 определена во всех точках, кроме
определена во всех точках, кроме 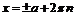 ,
, 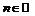 . В указанных точках
. В указанных точках 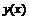 принимает значения
принимает значения 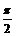 либо -
либо - 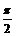 и не является дифференцируемой.
и не является дифференцируемой.
Если функция, производную которой нужно найти, упрощается после логарифмирования, целесообразно искать сначала не  , а
, а 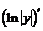 .
.
Пример 12. Найти производную функции
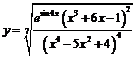 .
.
Функция определена при 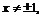
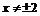 , причём
, причём 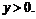
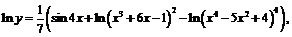
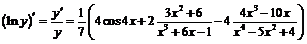
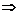
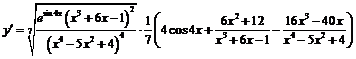 .
.
Другим приёмом, облегчающим дифференцирование, является введение промежуточной переменной.
Пример 13. Найти производную следующих функций:
1) 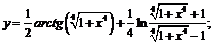
2) 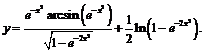
1) Пусть 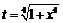 ,
, 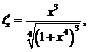 тогда
тогда 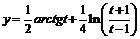 .
.
По правилу дифференцирования сложной функции получим:
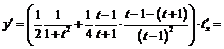
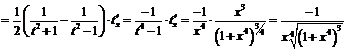
2) Пусть 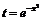 ,
, 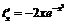 . Тогда
. Тогда 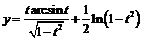 , и дифференцируя, получаем:
, и дифференцируя, получаем:
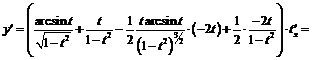
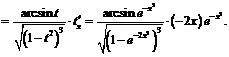

Пример 14. Установить формулу дифференцирования степенно-показательных выражений
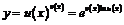 .
.
Дифференцируя это равенство как сложную функцию, получим
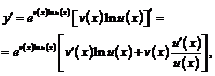
откуда
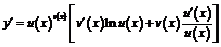 .
.
Этот же результат можно получить, дифференцируя равенство 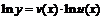 .
.
Пример 15. Найти 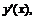 если
если 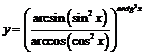 .
.
Функция 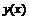 определена во всех точках числовой оси, кроме тех, где: 1)
определена во всех точках числовой оси, кроме тех, где: 1) 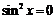
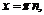
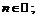
2) 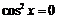
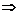
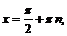
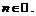
Логарифмируя, получим:
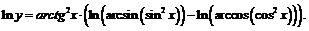 Тогда
Тогда
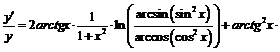
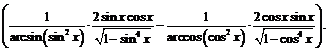
Так как
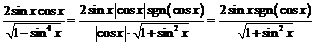
и 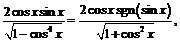 то выражение для производной примет вид:
то выражение для производной примет вид:
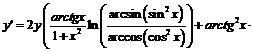
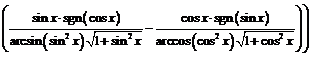 ,
,
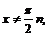
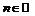 .
.
Пример 16. Установить, при каком условии функция 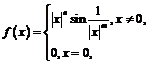
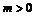 имеет: а) ограниченную производную в окрестности начала координат; б) неограниченную производную в этой окрестности.
имеет: а) ограниченную производную в окрестности начала координат; б) неограниченную производную в этой окрестности.
Найдём 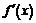 в окрестности точки
в окрестности точки 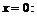
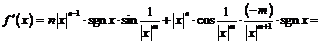
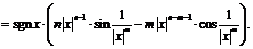
Для нахождения производной в точке 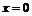 используем определение:
используем определение: 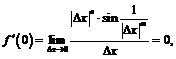 только если
только если 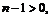
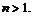
а) Очевидно, 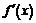 ограничена в окрестности точки
ограничена в окрестности точки 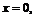 когда
когда 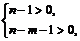 откуда следует
откуда следует 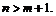
б) Из формулы для производной следует, что 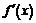 будет неограниченной, если
будет неограниченной, если 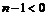 , либо
, либо 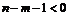 , либо и то, и другое одновременно. Так как
, либо и то, и другое одновременно. Так как 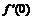 существует только при
существует только при 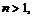 то производная является неограниченной в окрестности точки
то производная является неограниченной в окрестности точки 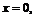 если
если 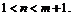
Пример 17. Показать, что функция
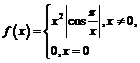 имеет точки недифференцируемости в любой окрестности точки
имеет точки недифференцируемости в любой окрестности точки 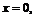 но дифференцируема в этой точке.
но дифференцируема в этой точке.
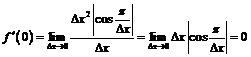 - производная в точке
- производная в точке 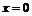 существует. Функция
существует. Функция 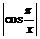 не имеет производной в точках, где
не имеет производной в точках, где 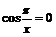 , т.е. при
, т.е. при 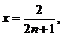
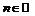 . Тогда
. Тогда
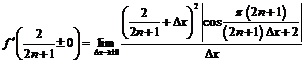 .
.
Так как
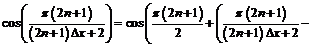
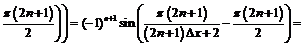
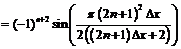 , то:
, то:
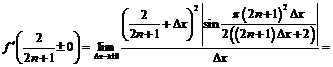
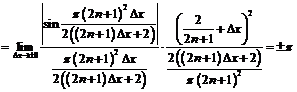 .
.
Пример 18. Исследовать на дифференцируемость функции:
1) 
2) 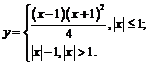
1) Данная функция ограничена и непрерывна на  . Дифференцируя, получим:
. Дифференцируя, получим: 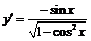 . В точках, где
. В точках, где 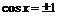 , т.е. при
, т.е. при 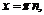
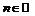 производная не существует. Действительно, сделав замену
производная не существует. Действительно, сделав замену 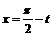 , получим:
, получим: 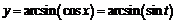 . В точках
. В точках 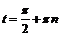 ,
, 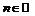 будем иметь:
будем иметь: 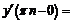
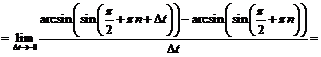
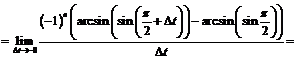
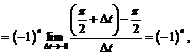
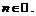
Если же 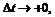 то
то 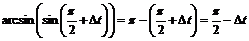 , поэтому
, поэтому 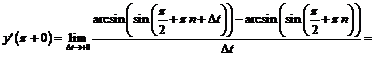
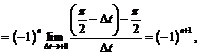
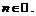
2) На промежутке 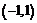 производная равна
производная равна
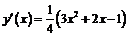 , на промежутке
, на промежутке 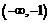
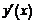 постоянна и равна -1, а на промежутке
постоянна и равна -1, а на промежутке 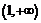 -
- 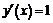 . В точках
. В точках 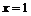 и
и 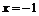 найдём
найдём 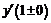 и
и  по определению:
по определению:
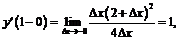
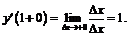
В точке 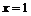 левая и правая производные существуют и равны 1, т.е. функция дифференцируема в этой точке.
левая и правая производные существуют и равны 1, т.е. функция дифференцируема в этой точке.

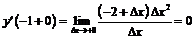 . Следовательно, функция не дифференцируема в точке
. Следовательно, функция не дифференцируема в точке 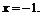
Пример 19. Доказать, что если функция 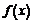 дифференцируема и
дифференцируема и 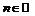 , то
, то 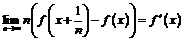 . Обратно, если для функции существует указанный предел, то можно ли утверждать, что эта функция имеет производную? Рассмотреть функцию Дирихле.
. Обратно, если для функции существует указанный предел, то можно ли утверждать, что эта функция имеет производную? Рассмотреть функцию Дирихле.
Так как функция дифференцируема, то существует предел 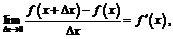 поэтому если положить
поэтому если положить 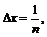
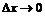 при
при 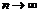 то будет существовать и предел
то будет существовать и предел 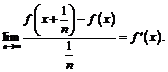 Однако существование последнего предела не означает наличия производной в точке
Однако существование последнего предела не означает наличия производной в точке 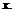 Действительно, для функции Дирихле
Действительно, для функции Дирихле 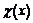 при
при 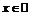 также и
также и 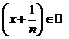 , поэтому
, поэтому 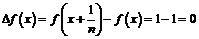 и указанный предел существует. Однако, если взять
и указанный предел существует. Однако, если взять 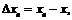 где
где 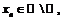
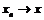 , то
, то 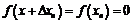 и
и 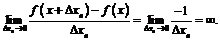 Следовательно, функция
Следовательно, функция 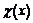 не имеет производной в любой точке
не имеет производной в любой точке 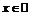 .
.
Пример 20. Для функции 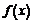 определить левую
определить левую 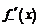 и правую
и правую 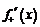 производные, если:
производные, если:
1) 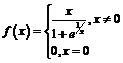 ;
;
2) 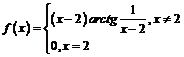 ; 3)
; 3) 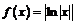
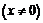 .
.
1) По правилам дифференцирования при 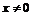 имеем:
имеем: 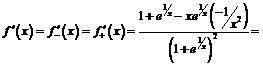
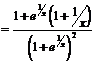 . В точке
. В точке  ищем левую и правую производные по определению:
ищем левую и правую производные по определению:
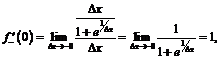
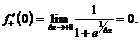
2) При 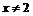 имеем:
имеем: 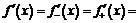
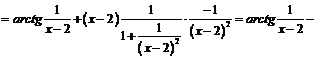
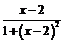 . В точке
. В точке 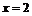 воспользуемся определением:
воспользуемся определением: 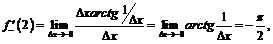
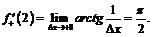
3) Так как 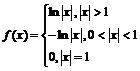 , то при
, то при 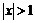
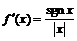 , а при
, а при 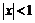
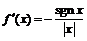 , откуда следует:
, откуда следует: 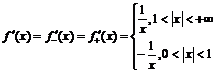 . В точках
. В точках 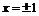 производная может быть найдена только по определению:
производная может быть найдена только по определению:
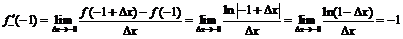
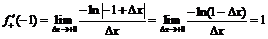 ,
,
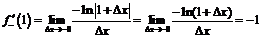 ,
,
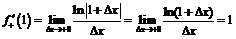 .
.
Пример 21. На сегменте 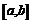 построить сопряжение двух полупрямых
построить сопряжение двух полупрямых 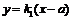
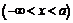 и
и 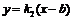
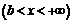 с помощью кубической параболы
с помощью кубической параболы 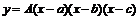 , где параметры
, где параметры 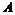 и
и 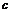 подлежат определению.
подлежат определению.
Коэффициенты 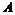 и
и 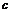 должны иметь такие значения, чтобы полученная функция была бы дифференцируемой в точках
должны иметь такие значения, чтобы полученная функция была бы дифференцируемой в точках 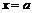 и
и 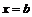 . Поэтому:
. Поэтому:
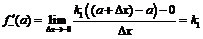 ,
,
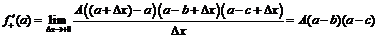 .
.
Аналогично для точки 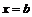 :
: 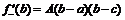 ,
, 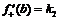 . Следовательно, необходимое сопряжение будет построено, если будут выполнены условия:
. Следовательно, необходимое сопряжение будет построено, если будут выполнены условия:
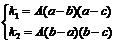 , откуда следует:
, откуда следует: 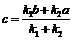 ,
, 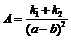 .
.
Пример 22. Можно ли утверждать, что сумма 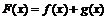 не имеет производной в точке
не имеет производной в точке 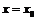 , если: а) функция
, если: а) функция 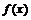 имеет в точке
имеет в точке 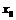 производную, а функция
производную, а функция 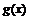 не имеет производной в этой точке; б) обе функции не имеют производной в точке
не имеет производной в этой точке; б) обе функции не имеют производной в точке 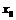 ?
?
а) Можно. Для этого необходимо рассмотреть предел
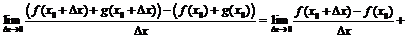
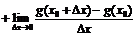 , а этот предел не существует, ибо не существует
, а этот предел не существует, ибо не существует 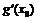 .
.
б) Нельзя. Например, функции 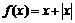 и
и 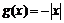 не имеют производной в точке
не имеют производной в точке 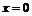 , а их сумма
, а их сумма 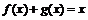 дифференцируема в этой точке.
дифференцируема в этой точке.
Пример 23. Может ли функция в точке разрыва иметь:
а) конечную производную; б) бесконечную производную?
а) Нет. Если функция дифференцируема в точке 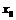 , то она непрерывна в этой точке.
, то она непрерывна в этой точке.
б) Да, например, для 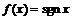 :
:
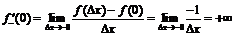 ,
, 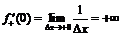 .
.
Пример 24. Можно ли почленно дифференцировать неравенство между функциями?
Нельзя. Например, 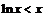 для
для 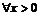 , но для производных этих функций
, но для производных этих функций 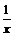 и
и 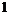 на интервале
на интервале 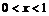 неравенство поменяет знак на противоположный.
неравенство поменяет знак на противоположный.
Пример 25. Доказать, что производная дифференцируемой периодической функции есть функция снова периодическая с тем же периодом.
Пусть 
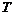 - периодическая функция. Тогда:
- периодическая функция. Тогда:
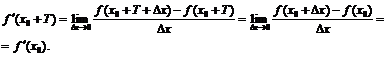
Пример 26. Определить области существования обратных функций 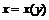 и найти их производные, если:
и найти их производные, если:
а) 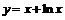
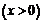 ;
;
б) 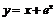 ; в)
; в) 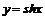 ; г)
; г) 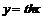 .
.
а) Множество значений данной функции есть множество  .
. 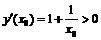 для
для 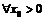 . Тогда областью определения обратной функции является вся числовая ось, а её производная равна:
. Тогда областью определения обратной функции является вся числовая ось, а её производная равна: 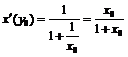 , где
, где 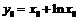 .
.
б) Функция непрерывна и монотонна на  , множество её значений - также вся числовая ось,
, множество её значений - также вся числовая ось, 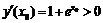 . Следовательно, обратная функция определена и непрерывна на
. Следовательно, обратная функция определена и непрерывна на  , а её производная равна:
, а её производная равна: 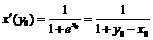 , где
, где 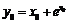 .
.
в) Функция 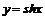 непрерывна и монотонна на
непрерывна и монотонна на 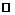 , обратная функция также определена на множестве вещественных чисел. Так как
, обратная функция также определена на множестве вещественных чисел. Так как 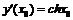 , то
, то 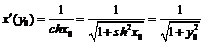 , где
, где 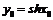 .
.
г) Функция 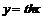 определена и монотонна на
определена и монотонна на 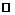 , обратная функция также определена на множестве
, обратная функция также определена на множестве 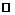 . Так как
. Так как 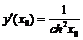 , то
, то 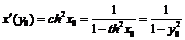 .
.
Пример 27. Выделить однозначные непрерывные ветви обратных функций 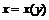 и найти их производные, если
и найти их производные, если 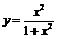 .
.
Функция определена и непрерывна на  . Её производная
. Её производная 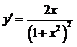 положительна при
положительна при 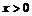 и отрицательна при
и отрицательна при 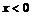 . Следовательно, на интервалах
. Следовательно, на интервалах 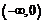 и
и 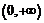 существуют дифференцируемые обратные функции. Обозначим эти функции
существуют дифференцируемые обратные функции. Обозначим эти функции
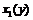 и
и 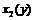 , тогда
, тогда 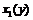 будет монотонно убывающей, а
будет монотонно убывающей, а 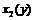 - монотонно возрастающей, так как
- монотонно возрастающей, так как 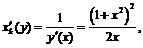
 . Для получения
. Для получения 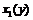 и
и 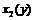 разрешим уравнение
разрешим уравнение 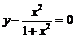 относительно
относительно 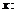
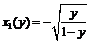
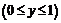 ,
, 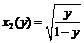
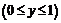 . При этом:
. При этом: 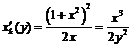 ,
, 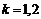 .
.