1. Пусть 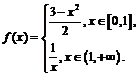 Определить промежуточное значение
Определить промежуточное значение 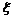 формулы конечных приращений для функции
формулы конечных приращений для функции 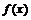 на сегменте
на сегменте 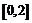 .
.
2. Доказать неравенства: а) 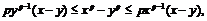 если
если 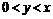 и
и 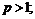 б)
б) 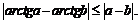
3. Найти на кривой 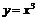 точку, касательная в которой параллельна хорде, соединяющей точки
точку, касательная в которой параллельна хорде, соединяющей точки 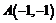 и
и 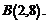
4. Верна ли формула конечных приращений для функции 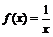 на сегменте
на сегменте 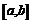 , если
, если 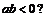
5. Найти функцию 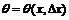 такую, что
такую, что 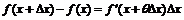 ,
, 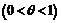 , если: а)
, если: а) 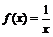 ;
;
б) 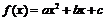
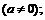 в)
в) 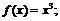 г)
г) 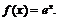
6. Пусть функция 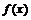 имеет непрерывную производную в интервале
имеет непрерывную производную в интервале 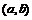 . Можно ли для всякой точки
. Можно ли для всякой точки 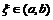 указать две другие точки
указать две другие точки 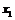 и
и 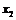 из этого интервала такие, что
из этого интервала такие, что
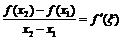
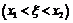 ?
?
Рассмотреть пример: 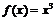
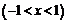 , где
, где 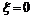 .
.
7. Доказать, что если функция 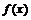 дифференцируема, но не ограничена на конечном интервале
дифференцируема, но не ограничена на конечном интервале 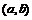 , то её производная
, то её производная 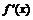 также не ограничена на интервале
также не ограничена на интервале 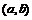 . Обратная теорема неверна (построить пример).
. Обратная теорема неверна (построить пример).
8. Показать, что для функции 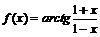
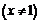 и
и  существует конечный предел
существует конечный предел 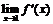 , однако функция
, однако функция 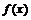 не имеет односторонних производных
не имеет односторонних производных 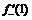 и
и  . Дать геометрическую иллюстрацию этого факта.
. Дать геометрическую иллюстрацию этого факта.
9. Доказать неравенства: а) 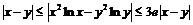 ,
, 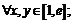 б)
б) 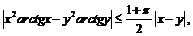
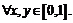
10. Доказать неравенства: а) 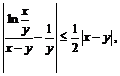
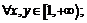
б) 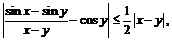
Производные и дифференциалы высших порядков
Определение.
Пусть функция 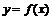 имеет конечную производную
имеет конечную производную 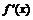 в некотором промежутке
в некотором промежутке 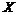 . Если функция
. Если функция 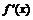 дифференцируема в точке
дифференцируема в точке 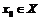 , то производная от производной называется второй производной функции
, то производная от производной называется второй производной функции 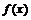 в указанной точке (или производной второго порядка) и обозначается
в указанной точке (или производной второго порядка) и обозначается
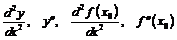 .
.
Так как скорость точки есть производная от пути S по времени 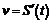 , ускорение a есть производная от скорости
, ускорение a есть производная от скорости 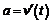 , то ускорение является второй производной от пути по времени.
, то ускорение является второй производной от пути по времени.
Аналогично, если функция 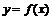 имеет вторую производную в промежутке
имеет вторую производную в промежутке 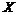 , то ее производную, конечную или нет, называют третьей производной или производной третьего порядка и обозначают
, то ее производную, конечную или нет, называют третьей производной или производной третьего порядка и обозначают
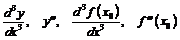 .
.
Определение.
Если 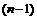 - я производная функции
- я производная функции 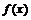 дифференцируема в точке
дифференцируема в точке 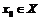 , то её производная называется производной n-го порядка или n-той производной от функции
, то её производная называется производной n-го порядка или n-той производной от функции 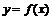 в точке
в точке 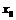 и обозначается:
и обозначается: 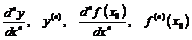 .
.
Таким образом, понятие n -той производной введено индуктивно посредством соотношения 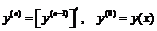 , которое называется рекуррентным.
, которое называется рекуррентным.
При вычислении производных высших порядков необходимо использовать все правила дифференцирования. Кроме того, имеет место следующая важная теорема.
Теорема.
Пусть функции 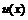 и
и 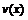 имеют в точке
имеют в точке 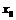 производные
производные 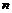 -го порядка, тогда функции
-го порядка, тогда функции 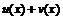 ,
, 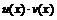 также имеют производные
также имеют производные 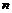 -го порядка в точке
-го порядка в точке 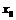 , причём:
, причём:
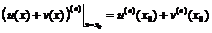 ,
,
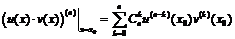 .
.
Последняя формула называется формулой Лейбница.
Введенный индуктивно метод нахождения производной n -го порядка какой-либо функции требует знания всех предшествующих производных. Однако в некоторых случаях оказывается возможным установить такое представление для n -ой производной, которое зависит только от n, что дает возможность не находить предшествующие производные.
Пример 1. Найти производные 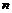 - го порядка от основных элементарных функций: а)
- го порядка от основных элементарных функций: а) 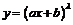 ; б)
; б) 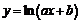 ;
;
в) 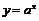 ; г)
; г) 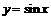 ; д)
; д) 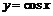 .
.
а) Рассмотрим функцию 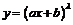 , где
, где 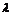 - любое вещественное число. Последовательно вычисляя производные, находим
- любое вещественное число. Последовательно вычисляя производные, находим
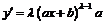 ,
, 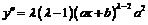 ,
,
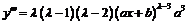 .
.
Легко усматривается общий закон
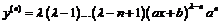 ,
,
который, вообще говоря, требует обоснования. Для этого воспользуемся методом математической индукции. Предполагая, что для данного n формула верна, продифференцируем её еще раз. Получим
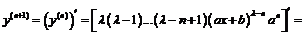
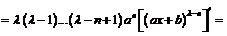
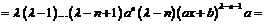
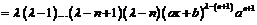 .
.
Т.е., наша формула оказывается верной и для (n +1)-ой производной. Откуда вытекает ее справедливость для всех значений n.
Если взять 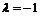 , то будем иметь:
, то будем иметь:
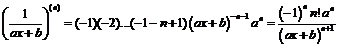 .
.
При 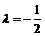 получим:
получим:
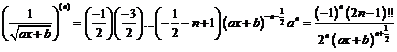
При натуральном 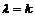 k -я производная будет постоянным числом k!; и все следующие производные окажутся нулями. Ясно, что
k -я производная будет постоянным числом k!; и все следующие производные окажутся нулями. Ясно, что 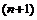 - я производная многочлена степени n также будет нулем.
- я производная многочлена степени n также будет нулем.
б) Для функции 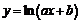 предварительно возьмем ее первую производную
предварительно возьмем ее первую производную 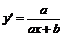 . Взяв
. Взяв 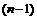 -ю производную от обеих частей данного равенства и воспользовавшись результатом предыдущего примера (случай
-ю производную от обеих частей данного равенства и воспользовавшись результатом предыдущего примера (случай 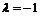 ), получим:
), получим:
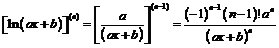 .
.
в) Для показательной функции имеем
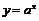 ,
, 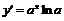 ,
, 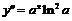 .
.
Приходим к общей формуле
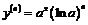 ,
,
легко доказываемой по методу математической индукции, в частности, 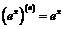 .
.
г)-д) Рассмотрим тригонометрические функции 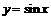 и
и 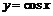 . Например, для
. Например, для 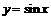 имеем:
имеем:
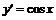 ,
, 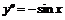 ,
, 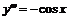 ,
, 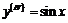 .
.
Для 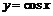
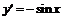 ,
, 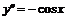 ,
, 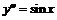 ,
, 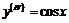 .
.
Если заметить, что каждое дифференцирование приводит к сдвигу аргумента на 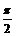 :
:
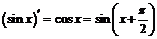 ,
, 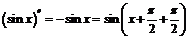 ,
,
то сразу находим
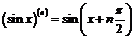 ,
, 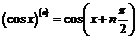 .
.
Пример 2. Пусть 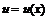 и
и  - дважды дифференцируемые функции. Найти
- дважды дифференцируемые функции. Найти 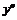 , если
, если 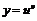
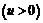 .
.
Используя правило дифференцирования показательно-степенной функции, последовательно получим: 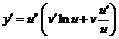 ,
,
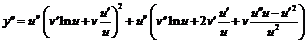 .
.
Пример 3. Пусть 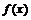 трижды дифференцируемая функция. Найти
трижды дифференцируемая функция. Найти 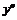 ,
,  , если
, если 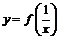 .
.
Применим правило дифференцирования сложной функции:
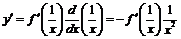 ,
, 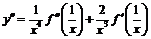 ,
,
 .
.
Пример 4. Найти 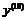 , если
, если 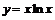 .
.
Воспользуемся формулой Лейбница, для этого положим: 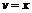 ,
, 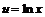 . Тогда
. Тогда 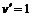 ,
, 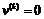 ,
, 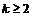 ;
; 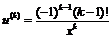 (пример 1б). Поэтому:
(пример 1б). Поэтому: 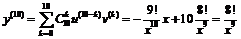 ,
, 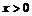 .
.
Пример 5. Найти 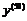 , если
, если  .
.
Пусть 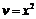 ,
, 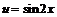 . Используя данные примера 1г, получим:
. Используя данные примера 1г, получим: 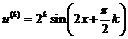 . Учитывая, что
. Учитывая, что 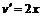 ,
, 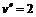 , а
, а 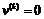 для всех
для всех 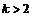 , будем иметь:
, будем иметь:
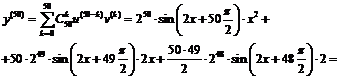
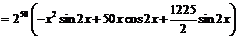 .
.
Отметим, что формула Лейбница особенно эффективна в том случае, когда одна из перемножаемых функций имеет лишь конечное число отличных от нуля производных, а вычисление всех производных другой функции не представляет затруднений.
Пример 6. Найти 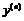 , если
, если 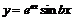 .
.
Чтобы найти n- тую производную функции 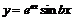 , предварительно вычислим ее первую производную
, предварительно вычислим ее первую производную
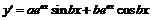 ,
,
которую, используя вспомогательный угол 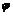 такой, что
такой, что
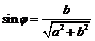 ,
, 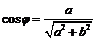 ,
,
можно представить в виде
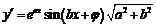 .
.
Замечая, что дифференцирование приводит к сдвигу на угол 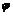 и умножению на
и умножению на 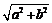 , устанавливаем общий закон
, устанавливаем общий закон
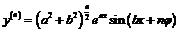 ,
,
обоснование которого осуществляется по методу математической индукции:
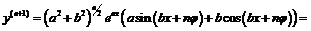
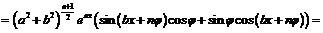
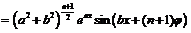 .
.
Пример 7. Найти 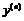 через
через 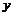 , если
, если 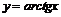 .
.
Для первой производной легко получим выражение через 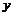 :
:
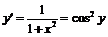 ,
, 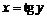 ,
,
Тогда:
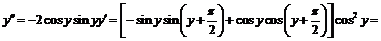
 .
.
Дифференцируя еще раз, находим:
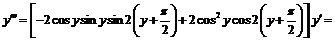
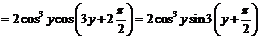 .
.
В результате приходим к общей формуле
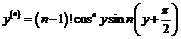 ,
,
для доказательства которой, опять-таки, используется метод математической индукции:
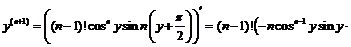
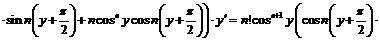
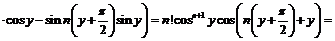
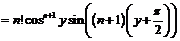 .
.
Применяя эту формулу, найдем значение 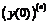 . Так как
. Так как 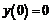 , то:
, то:
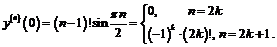
Пример 8. Найти 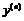 , если
, если 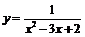 .
.
Разложим данную функцию на простые дроби:
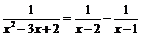 . По формуле, полученной в пример 1а, будем иметь:
. По формуле, полученной в пример 1а, будем иметь: 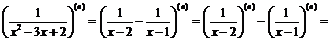
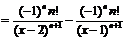 .
.
Определение дифференциала высших порядков.
Дифференциалом второго порядка или вторым дифференциалом функции  в некоторой точке называется дифференциал, вычисленный в этой точке от ее первого дифференциала:
в некоторой точке называется дифференциал, вычисленный в этой точке от ее первого дифференциала:
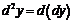 .
.
Все последующие дифференциалы определяются по индукции: 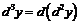 .Таким образом, дифференциалом
.Таким образом, дифференциалом 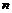 -го порядка или
-го порядка или 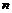 -м дифференциалом функции
-м дифференциалом функции  называется дифференциал от ее
называется дифференциал от ее 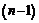 -го дифференциала:
-го дифференциала:
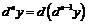 .
.
При вычислении дифференциалов высших порядков важно помнить, что 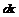 есть произвольное, малое или нет, и не зависящее от x число, которое при дифференцировании по x следует рассматривать как постоянный множитель. Тогда
есть произвольное, малое или нет, и не зависящее от x число, которое при дифференцировании по x следует рассматривать как постоянный множитель. Тогда
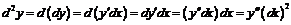 ,
,
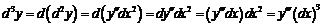 .
.
По индукции: 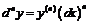 ,
, 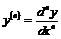 .
.
Последнее равенство показывает, что производную n -го порядка можно рассматривать как дробь.
Используя представление для дифференциала n -го порядка, преобразуем формулу Лейбница, умножив ее на 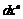 . Тогда получим
. Тогда получим
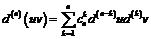 ,
, 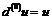 ,
, 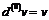 .
.
Поставим вопрос, переносится ли на дифференциалы высших порядков свойство инвариантности формы. Пусть функции  и
и 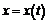 - достаточное число раз дифференцируемы. Составим сложную функцию
- достаточное число раз дифференцируемы. Составим сложную функцию 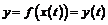 . Ее первый дифференциал можно записать в форме:
. Ее первый дифференциал можно записать в форме: 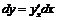 ,
, 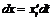 .
.
Вычислим второй дифференциал по 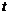 :
:
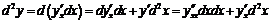 .
.
При этом мы воспользовались инвариантностью формы первого дифференциала. В результате 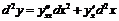 .
.
Если бы x была независимой переменной, то второй дифференциал имел бы вид: 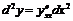 .
.
Таким образом, свойство инвариантности формы не имеет места для дифференциалов высших порядков. Для дифференциалов третьего и высших порядков число добавочных членов возрастает:
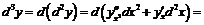
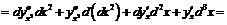

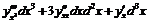 .
.
Пример 9. Пусть 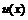 и
и 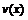 - дважды дифференцируемые функции. Найти
- дважды дифференцируемые функции. Найти 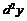 , если: 1)
, если: 1) 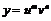 (
(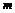 и
и 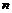 - постоянные); 2)
- постоянные); 2) 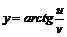 .
.
1) Используем определение первого и второго дифференциалов и правила дифференцирования:
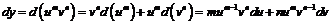 ,
,
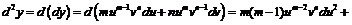
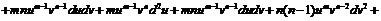
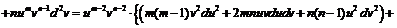
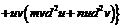 .
.
2) 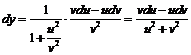 ,
, 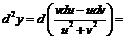
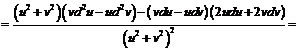
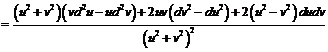 .
.
Пример 10. Найти 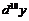 , если
, если 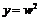 , где
, где 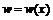 - функция переменной
- функция переменной 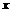 , дифференцируемая достаточное число раз.
, дифференцируемая достаточное число раз.
Для 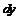 согласно свойству инвариантности формы получим:
согласно свойству инвариантности формы получим: 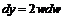 . Далее воспользуемся формулой Лейбница. Пусть:
. Далее воспользуемся формулой Лейбница. Пусть:
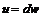 ,
, 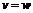 , тогда:
, тогда: 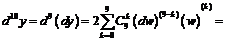
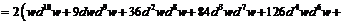
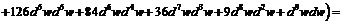
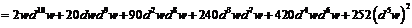 Пример 11. Выразить производные
Пример 11. Выразить производные 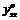 и
и 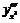 от функции
от функции 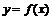 через последовательные дифференциалы переменных
через последовательные дифференциалы переменных 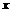 и
и 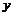 , не предполагая
, не предполагая 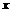 независимой переменной.
независимой переменной.
Последовательно находим:
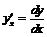 ,
, 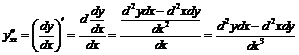 ,
,
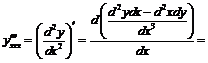
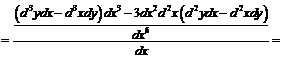
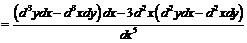 .
.
Эти формулы дифференцирования являются наиболее общими; если считать x независимой переменной, то все дифференциалы x, начиная со второго, оказываются нулями и мы приходим к уже известным формулам.
Формулы, полученные в предыдущем примере, позволяют осуществлять дифференцирование параметрически заданной функции:
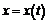 ,
, 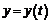 .
.
Предполагая наличие производных соответствующих порядков по t, находим: 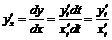 ,
,
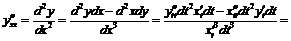
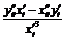 ,
,
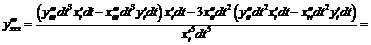
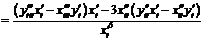 .
.
Пример 12. Найти производные 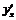 ,
, 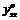 ,
, 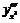 от следующих
от следующих
параметрически заданных функций: 1) 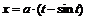 ,
, 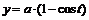 ; 2)
; 2) 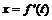 ,
, 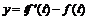 .
.
1) 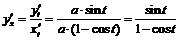 ,
,
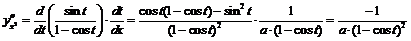
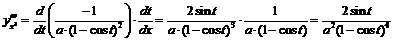
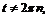
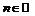 .
.
2) 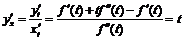 ,
, 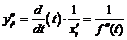 ,
,
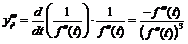 , при этом
, при этом 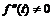 .
.
Формулы для нахождения производных высших порядков используются для упрощения выражений, содержащих производные высших порядков по одной переменной при переходе к новой переменной, и осуществляют замену переменной.
Пример 13. В выражении 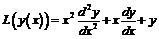 перейти от
перейти от 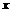 к новой переменной
к новой переменной 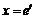 .
.
Так как 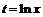 ,
, 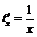 ,
,  , то
, то
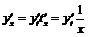 ,
, 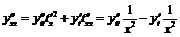 .
.
Подставляя эти равенства в исходное выражение, получим:
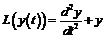 .
.
Пример 14. В выражении 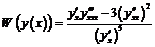 поменять ролями переменные x и y.
поменять ролями переменные x и y.
Используя формулы, полученные в примере 11 и учитывая, что роль переменной играет 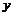 , а значит:
, а значит: 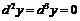 , будем иметь:
, будем иметь:
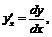
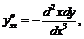
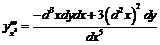 .
.
Следовательно, 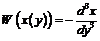 .
.