Если существует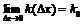 
, то прямая 
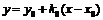, уравнение которой получается из уравнения секущей 
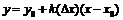при 
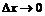, называется касательной к графику функции 
в точке 
.
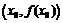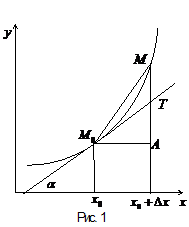Так как 
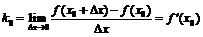, то функция 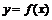имеет касательную в точке 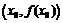тогда и только тогда, когда функция дифференцируема в точке 
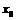, при этом 
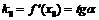, где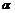 
- угол, образованный касательной с положительным направлением оси 
.
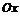Таким образом, уравнение касательной в точке 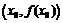имеет следующий вид: 
.
Если 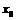придать приращение 
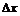, то ордината кривой получит приращение 
(
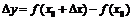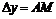на рис.1), а ордината касательной получит приращение 
(
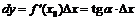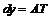на рис.1).
Пример 7. В каких точках кривой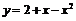 
касательная к ней а) параллельна оси 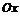; б) параллельна биссектрисе первого координатного угла?
Уравнение касательной к данной кривой в точке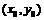 
имеет вид:
.
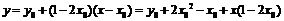а) Для того чтобы касательная была параллельной оси 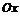, уравнение которой 
, необходимо, чтобы 
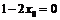, т.е. 
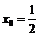. Таким образом, касательная параллельна оси 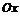в точке 
.
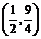б) Биссектриса первого координатного угла имеет уравнение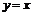 
, тогда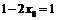 
, 
.
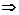
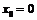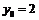Пример 8. Определить угол между левой и правой касательными к кривой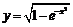 
в точке 
.
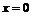Так как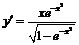 
при всех 
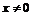, то в точке 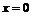производную следует искать по определению: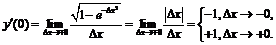 
Тогда уравнения левой и правой касательных в точке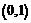 
будут иметь следующий вид: 
; 
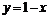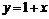. Очевидно, угол между левой и правой касательными в точке 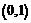равен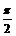 
.
Правило дифференцирования сложной функции и определение дифференциала приводят к важному свойству – инвариантности формы первого дифференциала.
Пусть даны функции 
и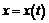 
. Составим из них сложную функцию 
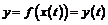. Если производные 
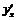и 
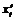существуют, то по правилу дифференцирования композиции функций имеем
.
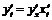Так как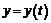 
, то для дифференциала 
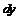получим выражение 
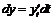. Заменяя 
ее выражением, находим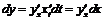 
, так как 
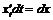. Таким образом, видно, что форма дифференциала сохраняется даже в том случае, когда аргументом является другая (дифференцируемая) функция. Это свойство и называется инвариантностью формы первого дифференциала.
Возможность выразить производную через дифференциал, взятый по любой переменной, приводит к тому, что формулы для нахождения производной сложной и обратной функций
, 
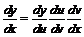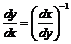
становятся обычными алгебраическими тождествами.
Определение.
Пусть функции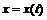 
и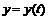 
определены в некоторой окрестности точки 
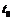и одна из них, например, 
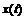, непрерывна и монотонна в указанной окрестности. Тогда в этой окрестности для функции 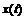существует обратная функция 
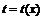, а в некоторой окрестности точки 
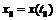имеет смысл суперпозиция 
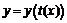, называемая параметрически заданной функцией.
Выведем формулу для дифференцирования параметрически заданной функции. В силу свойства инвариантности формы первого дифференциала будем иметь:
.
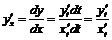Пример 9. Найти производные 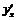следующих параметрически заданных функций: 1)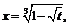 
;
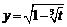2) 
, 
.
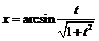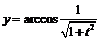1) Функция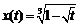 
определена и непрерывна при 
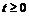, функция 
определена и непрерывна при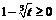 
, т.е. при 
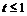. Производные этих функций, равные 
,
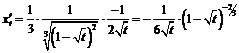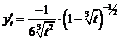обе определены и непрерывны, если 
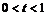, при этом 
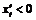. Следовательно, функция 
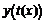определена на промежутке 
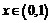. Её производная равна: 
.
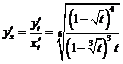2) Функции ,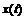 
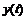определены и непрерывны на 
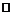. Найдём их производные: 
,
, 
.
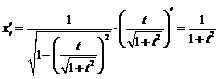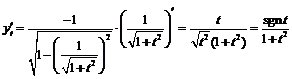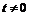Тогда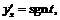 
.
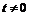Пример 10. Вывести формулу дифференцирования функции , заданной в полярных координатах.
Считая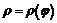 
, будем рассматривать соотношения 
, 
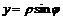как параметрические уравнения данной функции:
.
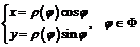Для дифференциалов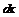 
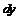и имеем
, 
,
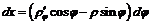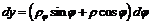откуда
.
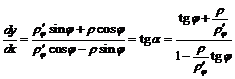Если ввести угол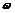 
между касательной к кривой и продолжением радиус-вектора точки, то получим:
.
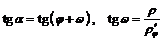Пример 11. Найти 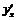, если: а) 
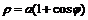; б)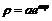 
.
а)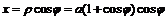 
, 
, 
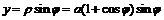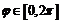. Найдём 
, 
:
, 
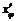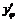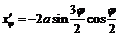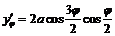. Тогда 
, 
.
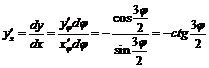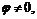
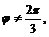
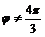б)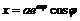 
, 
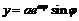. Тогда:
.
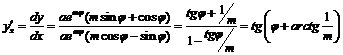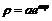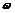Таким образом, для логарифмической спирали угол между касательной и радиусом-вектором точки касания является величиной постоянной и равен 
.
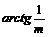Пример 12. Написать уравнение касательной к кривой
, 
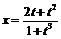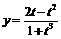в точках: а) 
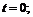б) 
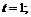в)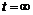 
.
Производная 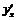равна: 
.
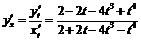а) В точке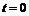 
, 
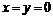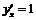, поэтому уравнение касательной имеет вид: ;
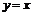б) При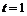 
, 
, 
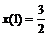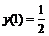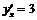, откуда следует уравнение касательной: 
;
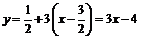в) Если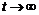 
, то и 
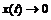, и 
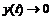, а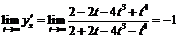 
. Следовательно, при 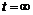имеем следующее уравнение касательной: 
.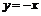