1. Для функции 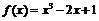 определить: 1)
определить: 1) 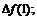 2)
2) 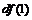 и сравнить их, если: а)
и сравнить их, если: а) 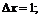 б)
б) 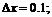 в)
в) 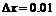 .
.
Найти дифференциал функции 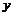 , если:
, если:
2. 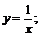 3.
3. 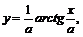
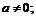 4.
4. 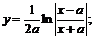 5.
5. 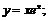 6.
6. 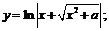 7.
7. 
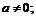 8.
8. 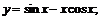 9.
9. 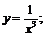 10.
10.  11.
11. 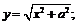 12.
12. 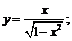
13. 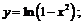 14.
14. 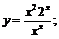 15.
15. 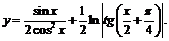
Пусть 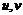 и
и 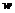 - дифференцируемые функции от
- дифференцируемые функции от 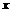 . Найти дифференциал функции
. Найти дифференциал функции 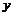 , если:
, если:
16. 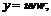 17.
17. 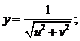 18.
18. 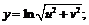 19.
19. 
20. 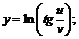 21.
21.  22.
22. 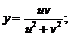 23.
23. 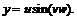
24. Доказать приближённую формулу: 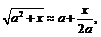
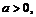 где
где 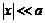 (
(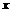 весьма мало по сравнению с
весьма мало по сравнению с 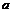 ). С помощью этой
). С помощью этой
формулы вычислить: а)  б)
б) 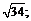 в)
в) 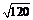 и сравнить с табличными данными.
и сравнить с табличными данными.
25. С какой относительной погрешностью можно измерить радиус 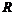 шара, чтобы объём его можно было определить с точностью до 1%?
шара, чтобы объём его можно было определить с точностью до 1%?
26. Определить абсолютную погрешность десятичного логарифма числа 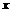 ,
, 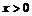 , если относительная погрешность этого числа равна
, если относительная погрешность этого числа равна 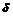 .
.
27. В круговом секторе радиус 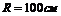 и центральный угол
и центральный угол 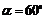 . Определить приближённо, насколько изменится площадь этого сектора, если: а) радиус его увеличить на 1 см; б) угол
. Определить приближённо, насколько изменится площадь этого сектора, если: а) радиус его увеличить на 1 см; б) угол 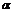 уменьшить на
уменьшить на 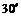 ?
?
Найти:
28. 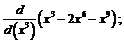 29.
29. 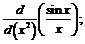 30.
30. 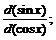
31. 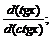 32.
32. 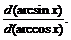
33. Написать уравнения касательной инормали к кривой  в точках: а)
в точках: а) 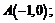 б)
б) 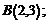 в)
в) 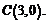
34. Доказать, что парабола 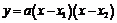
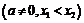 пересекает ось
пересекает ось 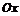 под углами
под углами 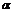 и
и 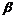
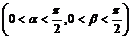 , равными между собой.
, равными между собой.
35. Под каким углом кривая 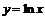 пересекает ось
пересекает ось 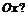
36. Под какими углами пересекаются кривые 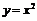 и
и 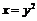 ?
?
37. Под какими углами пересекаются кривые 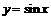 и
и 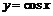 ?
?
38. При каком выборе параметра 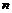 кривая
кривая 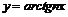
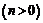 пересекает ось
пересекает ось 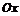 под углом, большим
под углом, большим 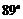 ?
?
39. Показать, что кривая 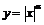 а) при
а) при 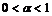 касается оси
касается оси 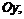 б) при
б) при 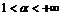 касается оси
касается оси 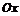 .
.
40. Доказать, что у астроиды 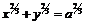 ,
, 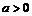 длина отрезка касательной, заключённого между осями координат, есть величина постоянная.
длина отрезка касательной, заключённого между осями координат, есть величина постоянная.
41. При каком соотношении между коэффициентами 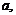
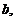
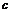 парабола
парабола 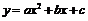 касается оси
касается оси 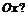
42. Доказать, что кривые 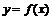
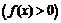 и
и 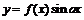 , где
, где 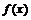 - дифференцируемая функция, касаются друг друга в общих точках.
- дифференцируемая функция, касаются друг друга в общих точках.
Найти производную 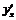 следующих параметрически заданных функций:
следующих параметрически заданных функций:
43. 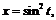
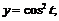 44.
44. 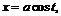
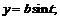 45.
45. 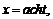
 46.
46. 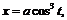
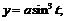 47.
47. 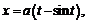
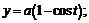 48.
48. 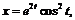
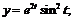 49.
49. 
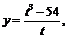
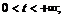 50.
50. 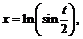
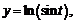
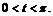
51. Найти 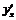 , если: а)
, если: а) 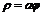 ; б)
; б) 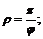 в)
в) 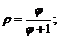
г) 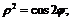 д)
д) 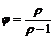 ; где
; где 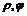 - полярные координаты.
- полярные координаты.
52. Показать, что функция 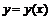 , определяемая системой уравнений
, определяемая системой уравнений 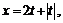
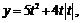 дифференцируема при
дифференцируема при 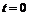 , однако её производная не может быть найдена по обычной формуле.
, однако её производная не может быть найдена по обычной формуле.
53. Написать уравнения касательной и нормали к кривой: 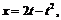
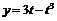 в точках а)
в точках а) 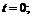 б)
б) 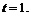
§3. Основные теоремы дифференциального исчисления
Теорема Ферма.
Пусть функция 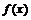 определена на промежутке X и во внутренней точке
определена на промежутке X и во внутренней точке 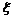 принимает наибольшее (наименьшее) значение. Если существует двусторонняя производная
принимает наибольшее (наименьшее) значение. Если существует двусторонняя производная 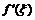 , то необходимо
, то необходимо 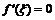 .
.
Геометрическое истолкование производной как углового коэффициента касательной приводит к тому, что если 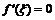 , то касательная к кривой в этой точке параллельна оси
, то касательная к кривой в этой точке параллельна оси 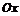 . Предположение, что точка
. Предположение, что точка 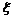 является внутренней, существенно, так как мы рассматриваем точки x справа и слева от
является внутренней, существенно, так как мы рассматриваем точки x справа и слева от 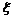 .
.
Теорема Ролля.
Пусть: 1) функция непрерывна на замкнутом промежутке 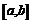 ; 2) дифференцируема во всех его внутренних точках; 3)
; 2) дифференцируема во всех его внутренних точках; 3) 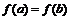 . Тогда найдется такая точка
. Тогда найдется такая точка 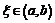 , что
, что 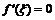 .
.
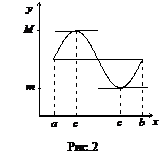 Геометрически теорема Ролля означает следующее: если крайние ординаты кривой равны, то внутри промежутка найдется точка
Геометрически теорема Ролля означает следующее: если крайние ординаты кривой равны, то внутри промежутка найдется точка 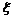 (одна или несколько), в которой касательная к кривой параллельна оси
(одна или несколько), в которой касательная к кривой параллельна оси 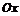 (рис. 2).
(рис. 2).
Пример 1. Функция 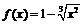 обращается в нуль при
обращается в нуль при 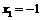 и
и 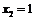 , но тем не менее
, но тем не менее  при
при 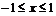 . Объяснить кажущееся противоречие с теоремой Роля.
. Объяснить кажущееся противоречие с теоремой Роля.
Противоречия с теоремой Роля нет, так как не выполнено условие 2 теоремы Роля: функция не дифференцируема в точке 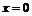 , хотя во всех других точках интервала существует конечная производная
, хотя во всех других точках интервала существует конечная производная 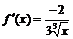 .
.
Теорема Лагранжа.
Пусть функция 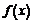 определена и непрерывна в замкнутом промежутке [a,b] и существует конечная производная в открытом промежутке (a,b). Тогда найдется такая точка
определена и непрерывна в замкнутом промежутке [a,b] и существует конечная производная в открытом промежутке (a,b). Тогда найдется такая точка 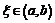 , что имеет место равенство
, что имеет место равенство
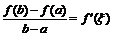 .
.
Эту теорему называют теоремой о среднем в дифференциальном исчислении. Теорема Ролля есть частный случай теоремы Лагранжа (условие 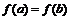 сразу дает
сразу дает 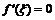 ).
).
Геометрическая интерпретация теоремы следует из сравнения левой и правой части равенства: левая часть дает угловой коэффициент хорды AB; правая же есть угловой коэффициент касательной к кривой в точке 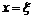 (рис. 3). Отсюда заключаем, что на дуге AB найдется, по крайней мере, одна точка M, в которой касательная параллельна хорде.
(рис. 3). Отсюда заключаем, что на дуге AB найдется, по крайней мере, одна точка M, в которой касательная параллельна хорде.
Выберем 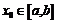 и придадим ему приращение
и придадим ему приращение 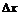 , не выводящее за пределы этого промежутка. К промежутку
, не выводящее за пределы этого промежутка. К промежутку 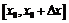
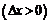 или
или 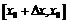
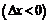 применим формулу Лагранжа. Число
применим формулу Лагранжа. Число 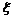 из промежутка
из промежутка 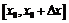 можно представить
можно представить
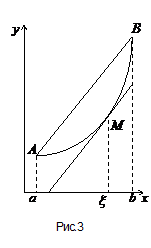 в виде
в виде 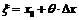 ,
, 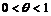 , тогда формула Лагранжа примет вид:
, тогда формула Лагранжа примет вид: 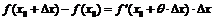 .
.
Полученная формула носит название формулы конечных приращений Лагранжа. Это равенство дает точное выражение для приращения функции при любом конечном приращении 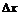 в отличие от приближенного
в отличие от приближенного 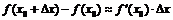 ,
,
погрешность которого стремится к нулю лишь при 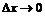 . И хотя величины
. И хотя величины 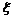 и
и 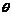 , вообще говоря, неизвестны, формула Лагранжа нашла многочисленные приложения в математическом анализе.
, вообще говоря, неизвестны, формула Лагранжа нашла многочисленные приложения в математическом анализе.
Из теоремы Лагранжа следует важное утверждение, позволяющее установить свойство производной.
Следствие. Пусть функция 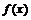 непрерывна в точке
непрерывна в точке 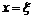 и имеет конечную производную всюду в правой (левой) полуокрестности точки
и имеет конечную производную всюду в правой (левой) полуокрестности точки 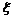 . Тогда, если производная
. Тогда, если производная 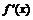 имеет в точке
имеет в точке 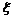 правое (левое) предельное значение, то это предельное значение равно правой (левой) производной в точке
правое (левое) предельное значение, то это предельное значение равно правой (левой) производной в точке 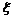 :
: 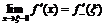 ,
, 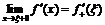 .
.
Отметим, что условие непрерывности функции в точке 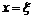 существенно. Например, для функции
существенно. Например, для функции 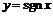 в точке
в точке 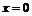 оно не выполнено, и функция не имеет в этой точке ни левой, ни правой конечных производных. Однако вместо условия непрерывности можно потребовать существования левой (правой) производной в самой точке
оно не выполнено, и функция не имеет в этой точке ни левой, ни правой конечных производных. Однако вместо условия непрерывности можно потребовать существования левой (правой) производной в самой точке 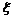 , что влечёт за собой непрерывность
, что влечёт за собой непрерывность 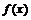 в точке
в точке 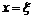 слева (справа).
слева (справа).
Данное следствие может быть использовано для нахождения односторонних производных.
Пример 2. Определить угол между левой и правой касательными к кривой  в точке
в точке 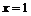 .
.
Так как
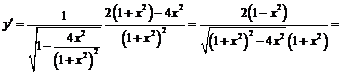
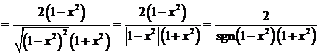 ,
, 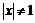 ,
,
то 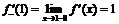 ,
, 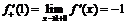 .
.
Тогда для левой и правой касательных в точке 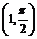 получим следующие уравнения:
получим следующие уравнения: 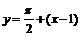 и
и 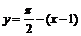 . Очевидно, что угол между этими прямыми равен
. Очевидно, что угол между этими прямыми равен 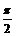 .
.
Из приведённого следствия вытекает важное свойство производной: если функция 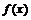 имеет конечную производную всюду на интервале
имеет конечную производную всюду на интервале 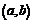 , то
, то 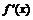 не может иметь на этом интервале ни точек устранимого разрыва, ни точек разрыва первого рода.
не может иметь на этом интервале ни точек устранимого разрыва, ни точек разрыва первого рода.
Приведём пример функции, производная которой существует и конечна всюду на некотором интервале и имеет в некоторой точке разрыв второго рода: 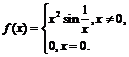
Для любого 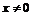 производная равна
производная равна 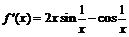 , в точке
, в точке 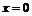 найдём
найдём 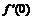 по определению:
по определению: 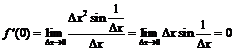 . Функция
. Функция 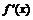 не имеет в точке
не имеет в точке 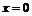 ни левого, ни правого пределов, ибо не существует
ни левого, ни правого пределов, ибо не существует 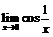 , следовательно, в точке
, следовательно, в точке 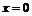 функция
функция 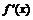 имеет разрыв второго рода.
имеет разрыв второго рода.
Теорема Коши. Пусть: 1) функции 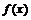 и
и 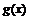 непрерывны в замкнутом промежутке
непрерывны в замкнутом промежутке 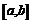 ; 2) функции имеют конечные производные, по крайней мере, в открытом промежутке; 3)
; 2) функции имеют конечные производные, по крайней мере, в открытом промежутке; 3) 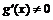 на
на 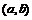 . Тогда найдется такая точка
. Тогда найдется такая точка 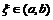 , что
, что
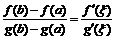 .
.
Очевидно, что теорема Лагранжа есть частный случай теоремы Коши и получается из последней при 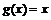 . Геометрическая иллюстрация ее такая же, что и для теоремы Лагранжа: на параметрически заданной кривой
. Геометрическая иллюстрация ее такая же, что и для теоремы Лагранжа: на параметрически заданной кривой 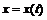 ,
, 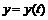 ,
, 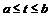 существует точка
существует точка 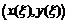 ,
, 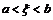 , в которой касательная параллельна хорде, соединяющей начало
, в которой касательная параллельна хорде, соединяющей начало 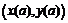 и конец
и конец 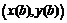 этой кривой:
этой кривой:
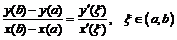 .
.
Пример 3. Объяснить, почему не верна теорема Коши для функций  и
и 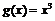 на сегменте
на сегменте 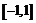 .
.
Так как в точке 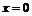 производные обеих функций обращаются в нуль:
производные обеих функций обращаются в нуль: 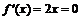 ,
, 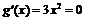 , то формула Коши неприменима.
, то формула Коши неприменима.
Теоремы Лагранжа и Коши с успехом применяются для доказательства равенств и неравенств.
Пример 4. Доказать неравенство: 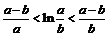 , если
, если 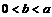 .
.
Рассмотрим функцию 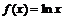 на отрезке
на отрезке 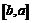 . По теореме Лагранжа получим:
. По теореме Лагранжа получим: 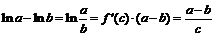 , где
, где 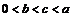 . Так как
. Так как 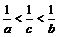 , то
, то 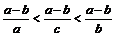 , откуда и следует требуемое неравенство.
, откуда и следует требуемое неравенство.
Пример 5. Пусть функция 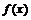 дифференцируема на сегменте
дифференцируема на сегменте 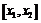 , причём
, причём 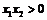 . Доказать, что
. Доказать, что 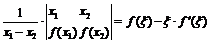 , где
, где 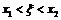 .
.
Преобразуем левую часть равенства:
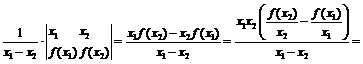
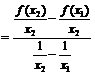 .
.
К функциям 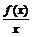 и
и 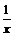 применим теорему Коши на отрезке
применим теорему Коши на отрезке 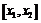 (её условия выполнены, ибо точка
(её условия выполнены, ибо точка 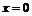 не принадлежит данному сегменту):
не принадлежит данному сегменту):
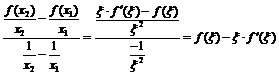 .
.
Равенство доказано.
Пример 6. Доказать тождество: 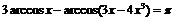 при
при 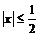 .
.
Так как  , а функция
, а функция 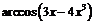 при
при 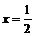 равна
равна 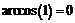 , то тождество примет следующий вид:
, то тождество примет следующий вид:
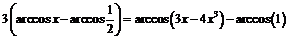 или
или
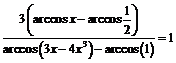 .
.
К функциям 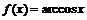 и
и 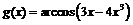 на отрезке
на отрезке 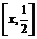 применим теорему Коши:
применим теорему Коши:
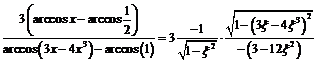 , где
, где 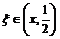 . Правая часть полученного равенства равна 1:
. Правая часть полученного равенства равна 1:
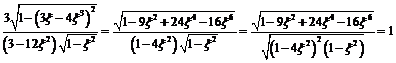 Тождество доказано.
Тождество доказано.
Пример 7. Доказать, что если функция 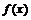 имеет в конечном или бесконечном интервале
имеет в конечном или бесконечном интервале 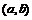 ограниченную производную
ограниченную производную 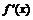 :
: 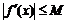 , то
, то 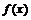 равномерно непрерывна на
равномерно непрерывна на 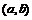 .
.
Из существования производной 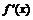 на
на 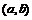 следует непрерывность функции на
следует непрерывность функции на 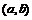 . Возьмем две произвольные точки
. Возьмем две произвольные точки 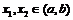 ,
, 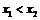 . Для промежутка
. Для промежутка 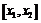 применим теорему Лагранжа
применим теорему Лагранжа
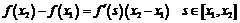 .
.
Тогда
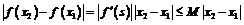 .
.
Выберем 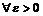 . Как бы ни была расположена пара точек
. Как бы ни была расположена пара точек 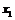 и
и 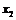 , лишь только
, лишь только 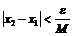 , так
, так 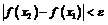 .
.
Теорема Кантора о равномерной непрерывности утверждает выполнение неравенства 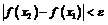 при условии
при условии 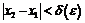 , но она доказывает лишь существование
, но она доказывает лишь существование 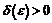 и не указывает, как оно должно быть мало. Для функции
и не указывает, как оно должно быть мало. Для функции 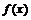 с ограниченной производной в качестве
с ограниченной производной в качестве 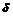 можно взять число
можно взять число  .
.