В линейной оптимизации целевая функция и все ограничения представляются линейными зависимостями. Однако, многие технические и экономические задачи оптимизации содержат выражения, не линейные относительно искомых величин. В этом случае мы имеем задачу нелинейной оптимизации, которая в общем виде может быть представлена как задача (2.1)-(2.2). Запишем эту задачу в векторной форме. Набор неизвестных будем обозначать вектором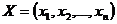 
. Тогда задача нелинейной оптимизации формулируется следующим образом. Найти вектор 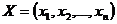, для которого
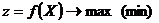
при ограничениях
, 
.
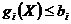Ограничения могут быть не только неравенствами, но также и равенствами. Условия неотрицательности неизвестных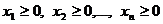 
, или 
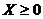, если они должны выполняться по смыслу задачи, могут быть включены в систему ограничений, а могут выписываться отдельно. Множество всех допустимых векторов будем называть допустимой областью в 
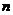-мерном векторном пространстве и обозначать буквой 
.
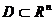Таким образом, в самом широком смысле общая задача нелинейной оптимизации заключается в отыскании экстремума целевой функции при заданных ограничениях в виде равенств или неравенств.
Переменные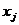 
, 
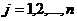, могут быть проектными параметрами некоторого процесса, показаниями приборов и т.д. Целевая функция может представлять собой стоимость, вес, прибыль и т.д. Ограничения составляются из ограниченности ресурсов, из технических требований, условий работы, пропускной способности, присущих процессу.
В задачах нелинейной оптимизации следует отличать понятие глобального экстремума от локального экстремума. Точка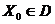 
называется точкой локального максимума (локального минимума) функции 
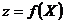, если найдется такая окрестность этой точки (на плоскости окрестностью может служить круг с центром в точке 
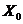), что для всех 
, принадлежащих 
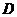и этой окрестности, выполняется неравенство 
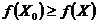(соответственно для локального минимума 
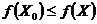). Для функции двух переменных можно привести простую геометрическую иллюстрацию понятий глобального и локального максимума (минимума) (рис.2.11). Графиком функции двух переменных 
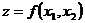является некоторая поверхность в трехмерном пространстве. Точка 
есть точка глобального максимума, , , 
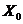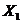– точки локального максимума этой функции.
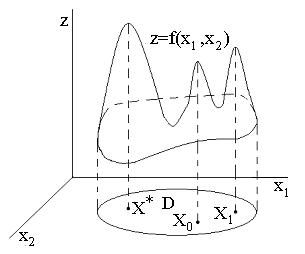
Рис. 2.11. Иллюстрация понятий глобального и локального максимума
Основные отличия нелинейной оптимизации от линейной оптимизации для задачи с двумя переменными (
) приведены в табл. 2.6.
Таблица 2.6
| Задачи линейной оптимизации | Задачи нелинейной оптимизации | |
| Вид допустимой области | Выпуклый многоугольник | Произвольная |
| Расположение допустимой области | I квадрант | На всей плоскости |
| Точка экстремума | Совпадает с вершиной области | Внутри или на границе области |
Задачи нелинейной оптимизации с двумя переменными в принципе могут быть решены графическим методом.
Пример 2.7. Требуется найти оптимальное решение следующей задачи
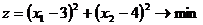
при ограничениях
.
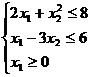Графическое решение показано на рис. 2.12.
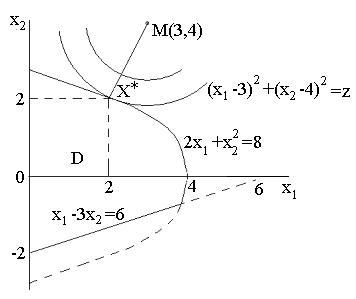
Рис. 2.12. Графическое решение примера 2.7
На основе неравенств системы ограничений строится допустимая область 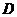. Линии уровня целевой функции есть окружности с центром в точке 
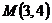. Окружность минимального радиуса, имеющая общие точки с областью, касается граничной линии (параболы 
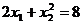) в точке 
. Эта точка и является оптимальным решением задачи минимизации, при этом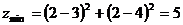 
.
Координаты оптимальной точки можно определить из условия коллинеарности нормальных векторов к окружности и параболе. Проекции нормалей на оси координат равны частным производным от соответствующих функций, то есть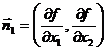 
и 
. Здесь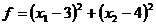 
, 
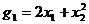. Поэтому 
, 
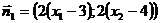. Из условия коллинеарности следует, что эти проекции должны быть пропорциональны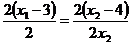 
. Решая систему уравнений
,
получим оптимальное решение задачи.