Задача распределения производственной программы относится к числу задач о комплектном выпуске продукции. Приведем пример такой задачи, интерпретируя ее как станковую задачу.
На двух станках могут обрабатываться детали трех видов. В течение рабочего дня на первом станке может быть обработано 30 деталей первого вида, или 30 деталей второго вида, или 42 детали третьего вида. На втором станке в течение рабочего дня может быть обработано 18 деталей первого вида, или 50 деталей второго вида, или 150 деталей третьего вида.
Пусть 2 детали первого вида, 5 деталей второго вида и 3 детали третьего вида составляют один полный комплект. Определить оптимальный план работы станков, то есть указать, какую часть рабочего дня каждый станок должен обрабатывать детали каждого вида с тем, чтобы число комплектов деталей было наибольшим.
Перечисленные данные запишем в табл. 2.10.
Таблица 2.10
| Станки | Детали | ||
| I | |||
| II | |||
| Комплектность | 2: 5: 3 |
Составим математическую модель станковой задачи. Пусть  – часть рабочего дня, в течение которой на
– часть рабочего дня, в течение которой на 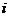 -м станке обрабатываются детали
-м станке обрабатываются детали 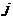 -го вида,
-го вида,  ,
,  . Тогда план работы станков можно представить таблицей
. Тогда план работы станков можно представить таблицей
 .
.
Обозначим через  число комплектов деталей, которое будет получено в соответствии с этим планом.
число комплектов деталей, которое будет получено в соответствии с этим планом.
Принимая рабочий день за единицу, получим, очевидно, следующую систему ограничений
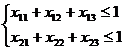 , (2.17)
, (2.17)
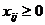 ,
,  ,
,  . (2.18)
. (2.18)
Чтобы составить целевую функцию, найдем количество деталей каждого вида, обработанных двумя станками по плану  :
:
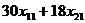 – количество деталей первого вида,
– количество деталей первого вида,
 – количество деталей второго вида,
– количество деталей второго вида,
 – количество деталей третьего вида.
– количество деталей третьего вида.
Так как один комплект состоит из 2 деталей первого вида, 5 деталей второго вида и 3 деталей третьего вида, то общее число комплектов деталей выражается функцией
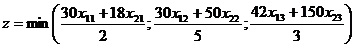 . (2.19)
. (2.19)
Таким образом, математической моделью станковой задачи является задача максимизации целевой функции (2.19) при условиях (2.17)-(2.18). Целевая функция  представляет собой минимум из трех линейных функций. Нетрудно доказать, что если функции
представляет собой минимум из трех линейных функций. Нетрудно доказать, что если функции  ,
, 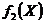 ,
, 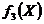 – линейны, то функция
– линейны, то функция 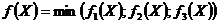 является вогнутой. Это утверждение рекомендуется доказать самостоятельно, исходя из определения вогнутой функции нескольких переменных. В случае функций одной переменной указанное утверждение можно пояснить геометрически. На рис. 2.17 представлены графики трех линейных функций (прямые линии) и минимум этих функций (жирная ломаная линия). Очевидно, что эта последняя функция вогнута.
является вогнутой. Это утверждение рекомендуется доказать самостоятельно, исходя из определения вогнутой функции нескольких переменных. В случае функций одной переменной указанное утверждение можно пояснить геометрически. На рис. 2.17 представлены графики трех линейных функций (прямые линии) и минимум этих функций (жирная ломаная линия). Очевидно, что эта последняя функция вогнута.

Рис. 2.17. Иллюстрация вогнутой функции
Тем самым задача (2.17)-(2.19) есть задача максимизации вогнутой функции  при линейных ограничениях, и, следовательно, она относится к выпуклому программированию.
при линейных ограничениях, и, следовательно, она относится к выпуклому программированию.
Рассмотрим два плана обработки деталей. По плану
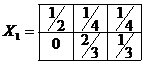
число комплектов деталей составляет
 .
.
Так как число комплектов должно быть целым, то считаем, что 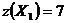 .
.
Второй план получим с помощью процедуры «Поиск решения» табличного процессора Excel. Математическая модель станковой задачи может быть сведена к задаче линейного программирования. Действительно, из определения целевой функции (2.19) следует, что
 ,
,  ,
, 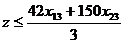 .
.
Поэтому, если включить  в число неизвестных, то после несложных преобразований получим следующую задачу
в число неизвестных, то после несложных преобразований получим следующую задачу
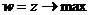
при ограничениях
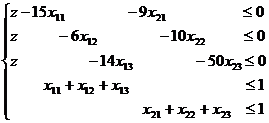 ,
,
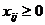 ,
,  ,
,  .
.
Результатом решения этой задачи в Excel служит оптимальный план обработки деталей
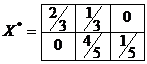 ,
,
для которого число полных комплектов равно 