Вспомним сначала определение выпуклых и вогнутых функций одной переменной. Функция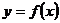 
называется выпуклой на некотором промежутке, если для любых двух точек из этого промежутка выполняется неравенство:
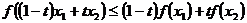
для любого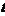 
, 
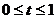(и вогнутой, если выполняется неравенство противоположного смысла).
Геометрически (рис.2.13) выпуклость функции означает, что хорда, соединяющая любые две точки графика функции, лежит выше соответствующей дуги кривой (для вогнутой функции (рис.2.14), наоборот, хорда лежит под соответствующим участком кривой).
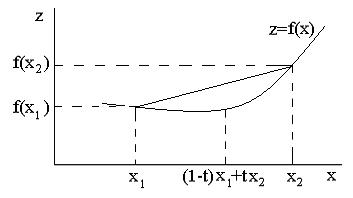
Рис. 2.13. График выпуклой функции одной переменной
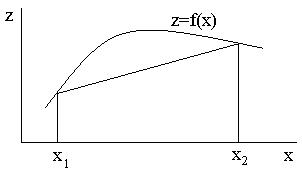
Рис. 2.14. График вогнутой функции одной переменной
Необходимым и достаточным условием выпуклости (вогнутости) дважды дифференцируемой функции 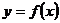одной переменной служит, как известно, неравенство 
(
).
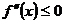Эти определения обобщаются на функции нескольких переменных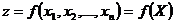 
, заданных в выпуклой области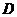 
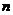-мерного векторного пространства. Пусть 
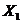и 
– две любые точки области 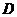, тогда в силу выпуклости отрезок, соединяющий эти точки, целиком лежит в области 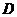. Это означает, что при любом 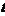, , 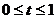точка 
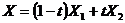принадлежит области определения функции 
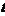, и когда пераметр меняется от 0 до 1, точка 
пробегает отрезок от точки 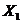до точки .
Функция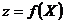 
называется выпуклой в выпуклой области 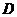, если для любых двух точек 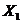и из области 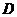выполняется неравенство
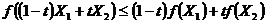
для любого , 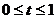. Функция 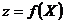называется вогнутой в выпуклой области 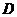, если для любых двух точек 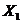и из области 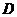выполняется неравенство
для любого , .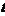
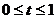Линейная функция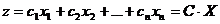 
, представляющая собой скалярное произведение векторов 
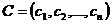и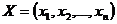 
, является одновременно и выпуклой и вогнутой во всем пространстве, так как для любых 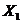, и справедливо очевидное равенство
.
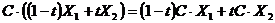Для выпуклых и вогнутых функций нескольких переменных имеют место следующие свойства:
· Если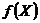 
– выпуклая функция, то функция 
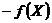вогнутая.
· Линейная комбинация выпуклых (вогнутых) функций с неотрицательными коэффициентами также является выпуклой (вогнутой) функцией, то есть, если функции 
, 
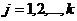выпуклые и числа 
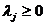, то функция
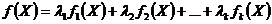
тоже выпуклая.
· Признак выпуклости приведем лишь для функции двух переменных. Если функция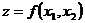 
дважды дифференцируема в выпуклой области, то она является выпуклой в том и только в том случае, когда выполняются неравенства:
(2.8)
(для вогнутой функции первое неравенство следует заменить на противоположное, а второе оставить без изменения).
· Пусть функция 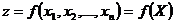определена в выпуклой области 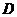и имеет непрерывные частные производные по всем аргументам. Для выпуклости функции необходимо и достаточно, чтобы для любых двух точек 
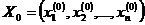и 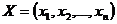области 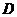было справедливо неравенство
(2.9)
(для вогнутой функции должно выполняться неравенство противоположного смысла).
Для функции одной переменной 
последнему свойству можно дать простую геометрическую иллюстрацию. В этом случае неравенство (2.9) записывается в виде
. (2.10)
Уравнение 
есть уравнение касательной к кривой в точке 
, поэтому согласно (2.10) касательная к выпуклой кривой всегда лежит ниже самой кривой (рис. 2.15).
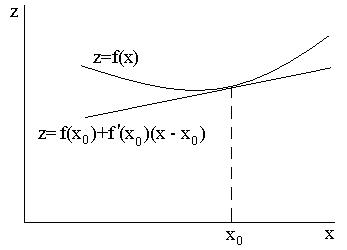
Рис. 2.15. Иллюстрация неравенства (2.10)
Пример 2.8. Определить, является ли выпуклой функция двух переменных
.
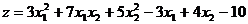Вычислим от функции частные производные первого и второго порядка. Получим
, 
,
, 
, 
.
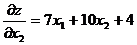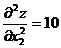Все частные производные второго порядка оказались постоянными функциями. Условия (2.8) для этих функций выполняются, поскольку
.
Следовательно, данная функция выпукла на всей плоскости.