Понятие о выпуклом программировании

Пусть функция 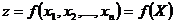определена и дифференцируема в выпуклой области 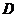. В любой точке локального экстремума функции, лежащей внутри области 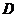, все частные производные обращаются в нуль. Такие точки называются стационарными. Определив стационарную точку, еще нельзя сказать, является ли она на самом деле точкой экстремума (локального или глобального), или вообще не является точкой экстремума. Поэтому для определения глобальных экстремумов требуется дополнительное, подчас очень сложное, исследование, включая, кроме того, и исследование на границе области. Однако, при отыскании глобального минимума выпуклой функции (или глобального максимума вогнутой функции) такое дополнительное исследование проводить не нужно. Точнее справедлива следующая теорема.

Теорема 1. Всякая стационарная точка 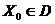выпуклой (вогнутой) функции 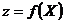является точкой глобального минимума (глобального максимума) этой функции.

Для максимума выпуклой (минимума вогнутой) функции имеет место следующее утверждение.

Теорема 2. Пусть функция 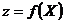выпуклая (вогнутая) в области 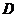, тогда ее глобальный максимум (глобальный минимум) достигается на границе области.

Справедливость обеих теорем в случае двух переменных легко подтверждается геометрически. На рис.2.16 представлен график выпуклой функции 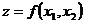. Стационарная точка 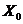(в этой точке касательная плоскость к поверхности параллельна плоскости 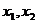) является точкой глобального минимума функции. Глобальный максимум функции достигается в граничной точке .

Рис. 2.16. График выпуклой функции двух переменных

На основании приведенных теорем оптимизация выпуклых и вогнутых функций значительно упрощается по сравнению с оптимизацией произвольных функций. Поэтому решение таких задач составляет содержание специального раздела – выпуклого программирования, в котором изучается задача минимизации выпуклых функций или максимизации вогнутых функций.

Теорема Куна-Таккера

Рассмотрим следующую задачу нелинейной оптимизации. Найти числа или вектор 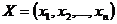, для которых

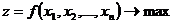(2.11)

при ограничениях

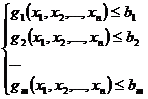, (2.12)

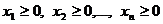. (2.13)

В векторной форме задача (2.11)-(2.13) представляется в виде

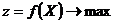(2.14)

при ограничениях

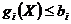, , (2.15)

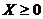. (2.16)

Допустим, что целевая функция (2.14) является вогнутой, а функции 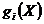, , входящие в систему ограничений (2.15) – выпуклы. Тогда нетрудно показать, что допустимая область задачи, определяемая системой (2.15 и (2.16, является также выпуклой. Тем самым поставленная задача есть задача максимизации вогнутой функции на выпуклом множестве, и, следовательно, она является задачей выпуклого программирования.

Дополнительно предположим, что допустимая область задачи удовлетворяет так называемому условию Слейтера, а именно: предположим, что в области 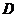существует точка 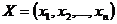такая, что , .

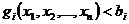Для задачи выпуклого программирования (2.14-(2.16) образуем функцию Лагранжа

,

где , , – множители Лагранжа. Будем писать для краткости 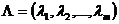. Тогда функция Лагранжа примет вид

.

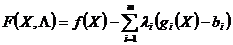Функции Лагранжа отводится важное место: при определенных условиях решение задачи выпуклого программирования сводится к отысканию седловой точки функции Лагранжа.

Пара 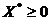, называется седловой точкой функции 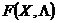, если выполняется неравенство

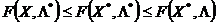
для всех , .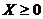

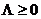Следующая теорема играет основную роль в математическом программировании.

Теорема (Куна-Таккера). Пусть в задаче выпуклого программирования (2.14)-(2.16) допустимая область удовлетворяет условию регулярности Слейтера. Тогда для оптимальности 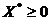необходимо и достаточно существования такого , чтобы пара была седловой точкой функции Лагранжа .

Весьма важным для практического использования является следствие из теоремы Куна-Таккера, которое определяет необходимое и достаточное условие существования седловой точки у функции Лагранжа, а, значит, и условие оптимальности допустимого решения задачи выпуклого программирования.

В предположении дифференцируемости функций и 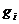, , входящих в задачу (2.14)-(2.16), запишем две системы неравенств по следующей схеме (табл. 2.7).

Таблица 2.7

Система неравенств I	Система неравенств II
...	...
...	...

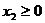
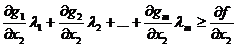
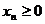
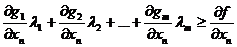
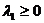
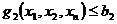
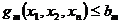
Система неравенств I есть совокупность условий (2.12)-(2.13). Система II определяет систему ограничений двойственной задачи. Будем, как и для линейного программирования, два неравенства, записанные в одной строке, называть сопряженными парами условий.

Используя обозначение для функции Лагранжа, указанные системы неравенств можно переписать в сокращенном виде (табл. 2.8).

Таблица 2.8

I	II
	,
	,

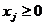
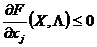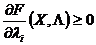
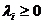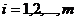
Следствие. Пусть функции и 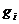, задачи выпуклого программирования (2.11)-(2.13) непрерывно дифференцируемы при 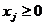, , и система ограничений (2.12) удовлетворяет условию регулярности Слейтера. Тогда для оптимальности допустимого решения необходимо и достаточно, чтобы существовало 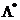, удовлетворяющее системе неравенств II, и такое, что в каждой паре сопряженных условий напротив строгого неравенства стояло бы равенство. Другими словами, должны выполняться соотношения

, ,

, .

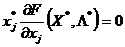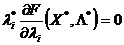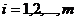Пример 2.9. Определить, является ли оптимальным решением для следующей задачи нелинейной оптимизации

при ограничениях

,

.

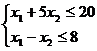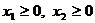Нетрудно видеть, что целевая функция вогнута. Система ограничений линейна и потому представляет собой выпуклую область. Ориентируясь на табл. 2.6, запишем неравенства данной задачи и напротив них соответствующие сопряженные условия (табл. 2.9)

Таблица 2.9

I	II

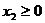
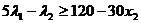
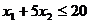
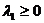
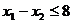
Видим, что является допустимым решением задачи. Для этого решения первое, второе и четвертое неравенства системы I выполняются как строгие, значит напротив должны стоять равенства, то есть

.

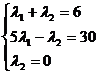Полученная система, очевидно, совместна, и ее решение , 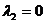удовлетворяет всем неравенствам системы II. Поэтому в силу следствия из теоремы Куна-Таккера заданное решение оптимально и .