Краткие теоретические основы уравнивания векторных измерений параметрическим способом.

УО Полоцкий государственный университет

Кафедра геодезии и кадастров

Электронные методические указания

К выполнению лабораторной работы №5

«Уравнивание и оценка точности трехмерных спутниковых измерений параметрическим

Способом»

По дисциплине

«Теория математической обработки геодезических измерений»

Для студентов 2 курса геодезического факультета

Автор: к.т.н., доцент Дегтярев Александр Михайлович

Версия 1

Новополоцк

2012 г

Оглавление

 

Введение и литература

1. Краткие теоретические основы уравнивания векторных измерений параметрическим способом.

1.1. Пример уравнивания трехмерных векторных измерений на основе прямой линейной формы параметрическим способом.

2. Оценка точности результатов уравнивания

2.1. Пример оценки точности результатов уравнивания.

3. Состав отчета

Цель работы: Уравнять трехмерную спутниковую сеть параметрическим способом на основе прямого подхода и выполнить точечную и интервальную оценку точности результатов уравнивания.

Время выполнения: 3 часа (1.5 пары).

 

Введение

С развитием геодезических измерительных наземных и космических систем (TotalStation, GNSS) все чаще для определения положения объектов земной поверхности используют так называемые векторные измерения, представляющие собой n- мерную связку, или вектор, чаще всего из 1, 2, или 3-ех приращений по элементам положения (координатам, высотам). Векторные измерения можно разделить на абсолютные, когда приращения получают относительно одной точки, принятой за исходную точку, и относительные, при которых приращения получают последовательно, от точки к точке. Кроме того, по размерности определяемых величин векторные измерения делят на одномерные (1D), или высотные; двухмерные (2D), или плановые; трехмерные (3D), или пространственные. Очевидно, что результат одного векторного измерения в этих случаях будет состоять из связки в 1, 2 и 3 приращения соответственно.

Очевидно, что матрица А уравнений поправок во всех случаях будет состоять из коэффициентов при соответствующих параметрах в уравнениях связи в виде чисел 0, 1 и –1 как и в нивелирных сетях, расширением по размерности которых и являются векторные измерения.

Простейшие векторные 1Dизмерения, это превышения в сети, полученные, например, электронным тахеометром. В этом случае используется линейная модель с константами и следующие из них параметрические уравнения поправок, а оценки параметров и измерений после уравнивания получают на основе формул общих формул параметрического способа.

 

 

Литература

1. Дегтярев А.М. Основы уравнительных вычислений. Электронный конспект лекций. – Новополоцк. 2011. –217 с.

2. Дегтярев А.М. Презентации к лекциям по дисциплине ТМОГИ. – Новополоцк. 2011.

3. Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработке геодезических измерений. – М.: Недра, 1984. –347 с.

4. Гудков В.М., Хлебников А.В. Математическая обработка маркшейдерско-геодезических измерений. – М.: Недра, 1990. –335 с.

5. Фан Хуан, Теория ошибок и метод наименьших квадратов. – Стокгольм, 2006. –287 с.

 

 

Краткие теоретические основы уравнивания векторных измерений параметрическим способом.

 

Задача оценивания результатов измерений в геодезических построениях состоит из:

– количественная сторона. Это получение однозначных и оптимальных значений определяемых величин, которая носит название уравнивание результатов измерений;

– качественная сторона. Это контроль точности (качества) результатов измерений и их функций, которая носит название оценка точности.

Для выполнения контроля качества измерений в геодезических построениях необходимо так скомбинировать измерения, чтобы возникали какие-либо математические условия. Возникновение математических условий приводит к наличию избыточных измерений и, поэтому – к задаче оценивания измерений в построении, так как неизвестно что взять в качестве конечного результата из нескольких значений, полученных из разных комбинаций измерений.

При обработке векторных плановых измерений (2Dизмерения), или пространственных измерений (3Dизмерения), одно векторное измерение представляет собой связку полученных приборно приращений для i -товой точки (D x, D y) _i, или (D x, D y, h) _i. Процедура обработки совершенно идентична, как и для 1Dизмерений, т.е. сетей нивелирования, но есть некоторые нюансы при формировании матрицы проектирования А системы уравнений поправок и при получении весовой матрицы Р. Некоторые из возможных вариантов:

1. Так как приращения есть функции элементарных измерений, таких как углы и расстояние, то, записав уравнения связи приращений и измерений, по обычной формуле (см. часть Оценка точности вектор-функции) получают блочную ковариационную матрицу (блоки 2´2, или 3´3 для каждой определяемой точки). Пересчитав ковариационную матрицу в матрицу весов, используют её в дальнейшей обработке.

2. После предобработки векторных данных программным продуктом фирмы-изготовителя прибора, обычно получают оценки точностных характеристик измерений: погрешность единицы веса, или дисперсионный фактор (дисперсия единицы веса), ковариационную, или корреляционную матрицу. Пересчитав имеющиеся точностные данные в матрицу весов, используют её в дальнейшей обработке.

Как видим, в обоих случаях требуется пересчет имеющихся точностных данные в матрицу весов, который может быть произведен следующим образом. Если дана ковариационная матрица измерений К_y, то на основе известной формулы , матрицу весов измерений получают в виде

. (1)

 

Если дана корреляционная матрица измерений R_y, то её пересчитывают в ковариационную матрицу измерений, а затем в весовую матрицу измерений следующим образом ,

 

. (2)

 

Здесь – дисперсионный фактор (дисперсия единицы веса), Матрица М – диагональная, у которой по диагонали размещены средние квадратические погрешности измерений (оценки стандартов измерений). Заметим, что в обоих случаях надо знать дисперсию единицы веса, хорошую её оценку, или быть достаточно уверенным, что она равна 1. В этом случае .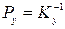

Рассмотрим трехмерные векторные космические измерения (3DGNSS). Здесь в результате спутниковых измерений получены приращения по трем координатам (X, Y, Z), (или (X, Y, H)) с точки на точку, которые являются измерениями. Измерения получены по линии между точкой стояния i и точкой наблюдения j, которые в совокупности называют связкой (или вектором) вида 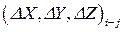в метрах, см. рис. 1. Получены также блоки ковариационных матриц размера 3´3 для каждой связки и дисперсионный фактор (дисперсия единицы веса).

 

 

 

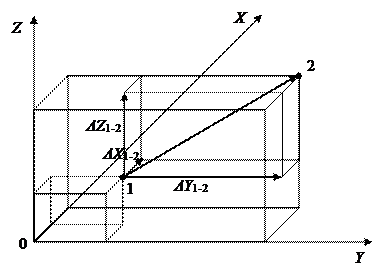Рис.1. Схема спутниковых векторных измерений (связка)

 

Процесс уравнивания векторных трехмерных измерений совершенно идентичен общей процедуре уравнивания:

- выяснить, возникает ли задача уравнивания, вычислив число избыточных измерений с учетом, что размерность построения 3;

- проверить качество измерений, учитывая, что число полигонов равно числу избыточных измерений деленное на размерность: r /3, а допуск обычно дается в ppm (part per million), или в миллионных долях числа. Например, 5 ppm это 5/1000000, или более привычное 1:200000;

- назначить параметры, выразить через них уравненные измерения и перейти к параметрическим уравнениям поправок. На этом этапе целесообразно в качестве параметров принимать уравненные элементы положения (так называемый прямой подход), т.е. трехмерные уравненные координаты всех определяемых точек . Тогда уравнения связи для уравненных результатов измерений будут как и при нивелировании. Например, для определяемых точек 1 и 2 (см. рис. 1) имеем для одного вектора (связки) 3 уравнения связи вида

Очевидно, что число уравнений равно утроенному числу определяемых пунктов.

Переход к параметрическим уравнением поправок производится по обычному правилу с учетом, что 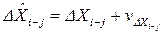и т.д. Тогда для первого уравнения связи вектора 1-2 из рис. 1, уравнение поправок будет

и т.д.

Из уравнений поправок выделяется матрица плана А и вектор свободных членов l для матричного представления уравнений v = A∙ + l. Здесь вектор состоит из уравненных координат точек

- решение переопределенной системы уравнений поправок v = A∙ + l по методу наименьших квадратов с получением системы нормальных уравнений

N∙ + b = 0, (3)

где 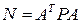- матрица системы нормальных уравнений, которая является квадратной с размером по числу определяемых параметров k×k (для нашего случая число определяемых точек умноженное на размерность 3), - вектор свободных членов системы нормальных уравнений размера k× 1. Матрица весов измерений Р имеет блочно-диагональный вид (блоки 3 × 3) и получена на основе правил определенных выше (см. (1), или (2)) по исходным точностным характеристикам (блочные ковариационные, или корреляционные матрицы и дисперсионный фактор). Наиболее целесообразный вид решения системы нормальных уравнений – через обратную матрицу

 

, (4)

Получая, таким образом, вектор уравненных координат точек .

– вектор уравненных измерений поучают после вычисления поправок в измерения v = A∙ + l обычным способом как измерение плюс поправка.

– контроль вычислений и уравнивания. Контроль вычислений производят на основе леммы Гаусса А ^Т Pv = 0. Иметь ввиду, что не выполнение леммы будет в основном из-за неверного вычисления поправок v. Для контроля выполнения процедуры уравнивания следует проверить известные положения из-за невыполнения (или появления) которых и возникла задача уравнивания:

а) сумма поправок по независимому полигону должна равняться невязке с противоположным знаком, т.е. уничтожать невязку – контроль вычисления поправок и уравнивания;

б) сумма уравненных измерений по независимому полигону не должна давать невязку, т.е. процедура уравнивания выполнена.

в) по уравненным параметрам получить все уравненные измерения.

г) координаты, вычисленные дважды по разным комбинациям уравненных измерений, должны быть одинаковыми и равняться уравненным значениям.

Обычно на практике все же чаще всего выполняют только проверку леммы Гаусса и как выполняются уравнения связи , т.е. получаются ли уравненные измерения по уравненным параметрам .

 

1.1. Пример уравнивания трехмерных векторных измерений на основе прямой линейной формы параметрическим способом.

 

В качестве примера уравняем результаты спутниковых трехмерных векторных измерений в сети рис. 2 на основе прямой параметрической формы.

Исходные данные для задачи в таблице и на схеме:

 

Таблица измерений и исходных координат

	исходные данные
	пункт	X	Y	Z
	П1	1133069.0028	4687779.3907	4137078.1319
	П2	1137976.0794	4689405.9259	4137005.0696
	П3	1136982.5698	4695408.8265	4136986.9436
	П4	1131848.5536	4693479.9487	4137096.1601
	измерения
вектор	сторона	ΔX	ΔY	ΔZ
	П1-Т2	1895.4517	3031.6299	33.3978
	Т2-Т1	6.0099	930.1085	-7.9197
	П2-Т2	-3011.6191	1405.0983	106.4703
	П3-Т2	-2018.1201	-4597.7998	124.5826
	П4-Т1	3121.9083	-1738.8228	7.4458

 

Измерения произведены до десятых долей миллиметра.

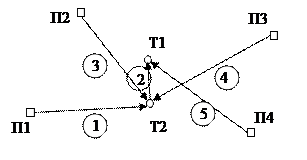
Рис. 1.2. Схема спутниковой трехмерной сети

Необходимые блоки ковариационных матриц K_ii по i-тым векторам (связкам):

0.3557 -0.1164 0.0851

K ₁₁= -0.1164 0.3344 0.1647 ×10^-4

0.0851 0.1647 0.4136

0.4309 -0.0231 0.0263

K ₂₂= -0.0231 0.4519 -0.0357 ×10^-4

0.0263 -0.0357 0.5063

0.1570 -0.1096 0.0204

K ₃₃= -0.1096 0.3022 -0.0103 ×10^-4

0.0204 -0.0103 0.2513

0.2608 0.1027 0.0288

K₄₄= 0.1027 0.1743 0.0544 ×10^-4

0.0288 0.0544 0.4251

0.4126 0.1435 0.1746

K₅₅= 0.1435 0.3093 0.0718 ×10^-4

0.1746 0.0718 0.3202

Общий вид ковариационной матрицы – блочно-диагональный с соответствующими 3×3 диагональными блоками и нулевыми недиагональными.

 

.

 

Полученный дисперсионный фактор м², или априорная погрешность единицы веса м (4 мм).

Замечание. Блоки ковариационной матрицы генерируются индивидуально в Matlab следующим образом:

randn(‘state’, sum(ГП*10*clock));

A = randn(20,3)*0.0015;

K=A′*A;