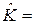Произвести 5 (по числу векторов) раз, обозначая сгенерированные блоки К11, К22 и. т.д.

1. Немного теории об уравнивании трехмерных спутниковых измерений (заполняется индивидуально).

2. Выяснить возникает ли задача уравнивания в сети. Задача обработки результатов измерений возникает по двум причинам:

– наличие избыточных измерений

– наличие неизбежных погрешностей измерений

Эти условия должны выполняться одновременно. Размерность построения d = 3, т.е. для однозначного определения положения одного пункта в поставленной задаче необходимо три величины. Всего определяемых точек (см. рис. 1) 2, трехмерных векторов – 5. Тогда имеем:

k = 2 ∙ 3 = 6– количество необходимых измерений;

n = 5 ∙ 3 = 15 – общее количество измерений;

r = n – k = 15 – 6 = 9 – количество избыточных измерений.

Учитывая то, что погрешности измерений, безусловно, присутствуют и что количество избыточных измерений не равно нулю – возникает задача уравнивания.

3. Проверка качества измерений. Как было определено выше, количество полигонов равно числу избыточных измерений r, делённое на размерность построения, т.е. 9: 3 = 3. Можно выделить следующие полигоны (см. рис. 1.2) по точкам:

1. П1 –Т2 –Т1 – П4

2. П2 –Т2 –Т1– П4 П – исходные; Т – определяемые.

3. П3 – Т2 –Т1 – П4.

Т. к. в качестве измерений имеем трёхмерные приращения по координатам, используем следующие формулы:

– для суммы приращений по осям практической

– для суммы приращений по осям теоретической.

Невязки вычислим по стандартным формулам:

Для контроля используем допуск на векторную (общую) невязку в каждом полигоне на основе следующей формулы:

 

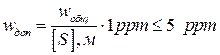, (5)

где 1 ppm = 1 000 000,5 ppm – 5 частей на миллион, или более удобно для нас – 1: 200 000, w_общ – общая невязка по полигону, полученная по частным осевым невязкам как

,

[ S ], м – сумма реальных трехмерных длин по полигону, каждая из которых вычисляется по приращениям векторов как

.

Результаты вычислений сведём в таблицу.

 

Таблица вычислений допусков по невязкам

		Невязки, м по осям	длины сторон, м
полигон	суммы и невязки	X	Y	Z	название стороны	длина
	Sтеор	-1220.4467	5700.5612	18.0323	П1-Т2	3575.56
	Sтеор	-6127.5175	4074.0296	91.1048	Т2-Т1	930.16
	Sтеор	-5134.0185	-1928.8685	109.1048	П2-Т2	3324.98
	Sпр	-1220.4492	5700.5578	18.0282	П3-Т2	5022.76
	Sпр	-6127.5258	4074.0228	91.0905	П4-Т1	3573.50
	Sпр	-5134.0162	-1928.8778	109.2165
	w	0.0025	0.0032	0.0041
	w	0.0083	0.0068	0.0143
	w	-0.0023	0.0093	0.0006
	wобщ	0.0058			wдоп, ppm	0.7 < 5
	wобщ	0.0179			wдоп, ppm	2.3 < 5
	wобщ	0.0096			wдоп, ppm	1.0 < 5

 

Как видно из низа последней колонки, общие невязки по всем трем полигонам не выходят за допустимые значения, т. е. измерения выполнены достаточно качественно.

4. Назначить параметры, выразить через них уравненные измерения и перейти к параметрическим уравнениям поправок. Параметры назначают по числу необходимых измерений k = 2 ∙ 3 = 6 в виде уравненных трехмерных координат для двух определяемых точек Т1 и Т2:

.

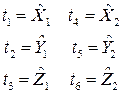Параметры образуют вектор столбец 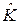из шести элементов.

Составляем уравнения связей всех уравненных измерений с уравненными параметрами:

1 вектор по стороне П1-Т2

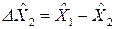
2 вектор по стороне Т2-Т1

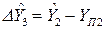3 вектор по стороне П2-Т2

4 вектор по стороне П3-Т2

5 вектор по стороне П4-Т1

 

Учитывая, что

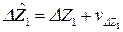и т.д.

запишем параметрические уравнения поправок для всех измерений по пяти векторам:

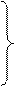
по 1 вектору

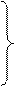
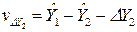по 2 вектору

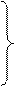
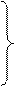
по 3 вектору

по 4 вектору

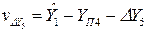по 5 вектору

Для представления уравнений поправок в общем, матричном виде как

v = A∙ 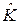+ l, где A размера (15´6) – матрица проектирования (плана), состоящая из коэффициентов 1, -1, 0 при параметрах, 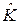- вектор уравненных координат точекразмера (6´1), l – вектор свободных членов системы уравнений поправокразмера (15´1), определенные выше уравнения поправок целесообразно свести в таблицу, обозначив вектор констант (исходных координат, выделенных в уравнениях поправок серым цветом) как с, а вектор измерений (см. исходные данные) как I:

 

Таблица получения матрицы А и свободных членов l

Уравнение поправок	параметры	вектор констант с, м	вектор измерений I, м	свободный член l = с - I, м
Т1	Т2
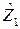
							-1133069.0028	1895.4517	-1134964.4545
							-4687779.3907	3031.6299	-4690811.0206
							-4137078.1319	33.3978	-4137111.5297
				-1				6.0099	-6.0099
					-1			930.1085	-930.1085
						-1		-7.9197	7.9197
							-1137976.0794	-3011.6191	-1134964.4603
							-4689405.9259	1405.0983	-4690811.0242
							-4137005.0696	106.4703	-4137111.5399
							-1136982.5698	-2018.1201	-1134964.4497
							-4695408.8265	-4597.7998	-4690811.0267
							-4136986.9436	124.5826	-4137111.5262
							-1131848.5536	3121.9083	-1134970.4619
							-469379.9487	-1738.8228	-4691741.1259
							-4137096.1601	7.4458	-4137103.6059

матрица проектирования А вектор l

5. Решение переопределенной системы уравнений поправок v = A∙ 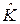+ l по методу наименьших квадратов на основе системы нормальных уравнений

N∙ 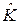+ b = 0. В системе - матрица системы нормальных уравнений размера 6 × 6, - вектор свободных членов системы нормальных уравнений размера 6 × 1. Для получения матрицы N и вектора свободных членов системы нормальных уравнений b необходимо по описанным правилам определить матрицу весов измерений Р на основе связи матрицы весов и заданной ковариационной матрицы , где σ₀ – погрешность единицы веса, равная 4 мм (см. исходные данные). Тогда для весов измерений имеем

а в числах (до 2 знаков после запятой достаточно), матрица весов Р будет

 

0,63	0,35	-0,27
0,35	0,79	-0,39
-0,27	-0,39	0,60
			0,37	0,02	-0,02
			0,02	0,36	0,02
			-0,02	0,02	0,32
						1,38	0,50	-0,09
						0,50	0,71	-0,01
						-0,09	-0,01	0,64
									0,80	-0,47	0,01
									-0,47	1,24	-0,13
									0,01	-0,13	0,39
												0,57	-0,20	-0,27
												-0,20	0,62	-0,03
												-0,27	-0,03	0,65

 

 

Теперь можно вычислить матрицу N нормальных уравнений

1.3700 -0.6761 -0.2594 -0.5709 0.2031 0.2658

-0.6761 1.8530 -0.1539 0.2031 -0.6179 0.0278

N =

-0.2594 -0.1539 1.043 0.2658 0.0278 -0.6509

-0.5709 0.2031 0.2658 2.9513 0.6631 -0.6448

0.2031 -0.6179 0.0278 0.6631 2.4760 -0.4025

0.2658 0.0278 -0.6509 -0.6449 -0.4025 2.2097

обратную к ней матрицу Q = N ^-1

1.0366 0.3697 0.2655 0.1574 -0.0399 -0.0125

0.3697 0.7524 0.2282 -0.0311 0.1689 0.0350

Q =

0.2655 0.2282 1.2811 -0.0217 0.0837 0.3515

0.1574 -0.0311 -0.0217 0.4167 -0.1199 0.0748

-0.0399 0.1689 0.0837 -0.1199 0.4938 0.0823

-0.0125 0.0350 0.3515 0.0748 0.0823 0.5940

и вектор свободный член b

1.2859e+006

-4.7410e+006

b =

1.0378e+006

5.1971e+006

8.1484e+006

4.2611e+006

 

Решение системы нормальных уравнений выполним через обратную матрицу

,

получая, таким образом, вектор 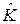уравненных координат точек до 4 знаков после запятой, как в исходных данных:

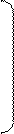1134970.4623

4691741.1276

4137103.6085, м

1134964.4536

4690811.0221

4137111.5302

 

6. Поправки в измерения получаем на основе матричного представления параметрических уравнений поправок v = A∙ 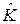+ l подстановкой полученных ранее элементов А, 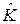и l также до 4 знаков после запятой, как в исходных данных:

 

-0.001

0.002

0.000

-0.001

-0.002

-0.010

0.004

-0.004, м

0.004

0.000

0.002

0.0027

-0.001

-0.003

-0.002

Уравненные измерения, как измерение плюс поправка представим в таблице.

Уравненные значения измерений:

сторона
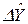
П1-Т2	1895.4500	3031.6330	33.3988
Т2-Т1	6.0086	930.1054	-7.9216
П2-Т2	-3011.6323	1405.0962	106.4606
П3-Т2	-2018.1161	-4597.8043	124.5866
П4-Т1	3121.9087	-1738.821	7.4484

7. Из контролей выполним:

- вычислительный, на основе леммы Гаусса

 

т.е. практически есть равенство нулю;

- основной и наиболее часто используемый контроль уравнивания, по которому из уравненных параметров 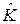точно получают уравненные измерения 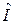, т.е. выполнение исходных теоретических уравнений связи. Эти уравнения в матричном виде есть . После подстановки в правую часть численных значений А, 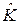и с, получаем вектор

1895.4500

3031.6330

33.3988

6.0086

930.1054

-7.9216

-3011.6323

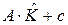= 1405.0962, м

106.4606

-2018.1161

-4597.8043

124.5866

3121.9087

-1738.821

7.4484

который в точности равен вектору уравненных измерений (см. таблицу выше).