Основой оценки точности результатов уравнивания при параметрическом способе обработки является ковариационная матрица K F, полученная на основе закона переноса ошибок для оцениваемой вектор-функции F (или одной функции f). При этом, необходимо чтобы оцениваемая функция выражалась через величины, ковариационная матрица которых известна. После уравнивания в подавляющем большинстве случаев оценивают уравненные измерения и уравненные параметры. Оцениваемые функции, как показала практика, проще выражать через уравненные параметры. Очевидно, что для них ковариационная матрица известна и равна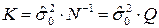 
. Из этой формулы следуют два равнозначных способа оценки точности:
- на основе ковариационной матрицы K;
- на основе обратной матрицы весов Q.
Рассмотрим более детально второй способ сплошной оценки точности. Для её выполнения выражаем оцениваемую вектор-функцию F через уравненные параметры. В нашей задаче это выражение вектор-функции F через уравненные координаты. Далее формируем матрицу F из коэффициентов при параметрах в выражении вектор-функции F через уравненные координаты и используем для второго случая закон переноса ошибок в виде
. (6)
Так как нас интересуют только погрешности, а не ковариации, то выделяем из формулы диагональные элементы, которые являются дисперсиями оцениваемых функций в вектор-функции F и извлекаем из них корень. Окончательно для средней квадратической погрешности i- той функции в вектор-функции F имеем
. (7)
Здесь 
- обратный вес i -той оцениваемой функции в общей вектор-функции F и который является просто диагональным элементом общей матрицы обратных весов Q F 
всех оцениваемых элементов в F.
Апостериорная (вычисленная по результатам уравнивания) погрешность единицы веса вычисляется по одной из известных формул
. (8)
Не сложно показать, что матрица коэффициентов F для оценки точности уравненных измерений есть матрица А системы параметрических уравнений поправок. Тогда для оценки точности i -того уравненного измерения на основе общей формулы имеем
. (9)
То есть, определяем обратную матрицу весов для уравненных измерений как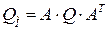 
, берём по очереди её диагональные элементы, извлекаем из них корень и умножаем на погрешность единицы веса 
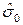, получая таким образом, по одной, все средние квадратические погрешности уравненных измерений.
Известно, что матрица коэффициентов F для оценки точности уравненных параметров есть единичная матрица Е, откуда для оценки точности i -того уравненного параметра по одному на основе общей формулы имеем
, (10)
так как 
. Здесь также определяем обратную матрицу весов для уравненных параметров как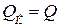 
, выделяем по одному её диагональные элементы, извлекаем из них корень и умножаем на погрешность единицы веса σ, получая, таким образом, по одной все средние квадратические погрешности уравненных параметров.
Следует иметь ввиду, что в результате оценки точности по (10) мы получаем погрешность определения положения по оси х, y и z для всех определяемых пунктов 
. Обычно окончательный результат оценки точности положения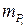 
i – той точки получают в виде одного числа – круговой погрешности Гельмерта вида
. (11)
Интервальная оценка точности выполняется на основе сплошной оценки точности уравненных измерений и уравненных параметров для вероятности 0.95, используя частные случаи общей формулы для произвольной истинной величины Х вида
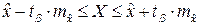. (12)
Тогда, если в качестве оцениваемой интервально величины принимается истинное значение координат, оцененных как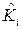 
и истинных измерений, оцененных как 
, имеем следующие формулы для доверительных интервалов:
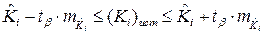, (13)
, (14)
по числу определяемых координат и измеренных приращений. В качестве доверительной вероятности обычно принимают (но не обязательно) Р = 0.95, а квантиль t -распределения Стьюдента вычисляют по исправленной для двухстороннего интервала вероятности вида β = (1 + Р)/2 и числу избыточных измерений.