построение картины плоскопараллельного поля. 8 глава

В ферромагнитных веществах резко сказываются явления гистерезиса, маг- нитной вязкости и ряд других. В силу этих причин ε, γ, μ оказываются функциями частоты и комплексами.

Убедимся в том, что вязкостные процессы при поляризации диэлектриков
с полярными молекулами приводят к тому, что ε становится комплексным
числом.

Обозначим —напряженность поля, обусловленную приложенным к конден- сатору напряжением u;.например, для плоского, конденсатора с. расстоянием d между обкладками Еп = u./d; Е_Д — действующая на диполи.полярных молекул напряженность поля, вызывающая их поворот.

За счет вязкостных процессов при поляризации (повороте) полярных молекум E_Д< E_п на величину, пропорциональную скорости поляризации:

* Зависимость параметров веществ от частоты впервые была обнаружена русским ученым В. К. Аркадьевым в 1908—1911 гг. Физическое объяснение этим явлениям было дано им в 1913 г. в работе «Теория электромагнитного поля в ферромагнитном металле».

 

Первое слагаемое правой части находится в фазе с приложенным напряжением, второе на 90° его опережает. Тангенс угла потерь, несовершенного диэлектрика (см.

§3.9) tgα = ε^П+γ/ω/ε Используя уравнение (16.34) § 16.8-для вязкостных процес­сов в ферромагнетиках, можно вывести аналогичные формулы и для.: комплексной магнитной проницаемости в предположении, что вихревые токи отсутствуют.

Заметим, что дифференциальное уравнение, описывающее процесс зарядки кон­денсатора с вязким диэлектриком через сопротивление R от источника постоянной; э. д. с, если учесть вязкостные процессы по уравнению (22.14), будет иметь вто­рой (не первый!) порядок.

Второе замечание. В § 22.2 рассматривалось первое уравнение Максвелла (22.1) В правой части этого уравнения записаны две плотности тока — проводимости и электрического смещения ε_а dE/dt. Но кроме токов проводимости и электрического смещения существует третий вид тока—ток переноса (это собирательное назва­ние).

Под током переноса понимают ток, природа которого отлична от природы тока проводимости и тока смещения, это, например, toк возникающий в электронной лампе вследствие явления термоэлектронной эмиссии. Плотность тока переноса равна объемной плотности переносимых зарядов ρ, умноженной на скорость их переноса ν. _

Если ток переноса создается движением со скоростью v₊ положительно заря­женных частиц с объемной плотностью р₊ и движущихся со скоростью v_ отрицательно заряженных частиц с объемной плотностью р., то плотность тока переноса равна
ρ₊ν₊+ р_- v _-Ток переноса, так же как и остальные виды токов, создает, магнитное поле.

С учетом тока переноса первое уравнение Максвелла записывают следующим образом:

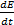rot H= +ε_а + pv.

^{1/₂5 Зак. 1730 129}

Для тех задач, которые рассматриваются в ч. III учебника, ток переноса отсутствует, поэтому первое уравнение Максвеллами взято в форме (22.1).

Третье замечание. При чрезвычайно высоких частотах, когда длина электромагнитной волны становится соизмеримой с линейными размерами, характеризующими молекулярную структуру самого вещества, вещество уже нельзя рассматривать как континуум. В этом случае уравнения Максвелла должны быть заменены уравнениями квантовой теории поля..

Четвертое замечание. В Курсе ТОЭ в основном рассматривают поля в изотропных линейных средах. В них вектор В = μ_аH совпадает по направлению с вектором H, вектор D = ε_а E совпадает по направлению с E и вектор 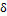= γЕ с Е. В изотропных средах μ, ε и γ представляют собой некоторые постоянные числа не зависящие от величины H или E (но зависящие от частоты). Если проекции вектора B на оси х, у,z обозначить В_х, В_у, В_z, а проекции H — через Н_х, Нγ, Н_z, то для изотропных сред В_х = μ_а H_x, В_у = μ_а H_γ, B_z = μ_а H_z. Аналогично, D_х = ε_аЕ_х; D_y= ε_аE_y; D_z = ε_аE_z и 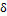_х = γЕ_х и т. д. В анизотропных средах В = μ_аH не совпадает по направлению с Н, D с Е, 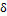с Е. Любая проекция В, D и 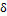зависит не только от одноименной проекции H или Е, но и от разноименныхи.проекций. Так, В_х зависит не только от Н_х, но и от H_y Н_z; B_x = μ_xx H_x + μ_ху Н_у + μ_xz H_z; аналогично, В_y = μ_ухН_х + μ_уу Н_у +μ _yzН_z, где μ_xx, μ_ух,, μ_xz — составляющие тензора магнитной проницаемости μ_а

Подобные выражения существуют и для тензоров ε_а и γ.

§ 22.9. Основные положения электродинамики движущихся сред (основы реля­тивистской электродинамики). Положим, что имеются две системы отсчета коорди­нат и времени. Одна система неподвижна, имеет начало в точке О, координаты про­извольной точки в ней х, у, z и время t (система О): Другая система отсчета связана с движущейся по отношению к предыдущей системе отсчета средой, имеет начало_: в точке O₁, a координаты той же точки в ней x_1; у₁, z₁и время t (система О_1). Допустим, что в момент времени t= 0 обе системы координат совпадают и что скорость движения среды v направлена по оси х. Тогда в соответствии с теорией относительности можно записать преобразования Лоренца, связывающие координаты и время в обеих системах отсчета:

где с — скорость света, β= v/с.

Обозначим напряженность электрического поля и магнитную индукцию в произвольной точке, которые бы измерил наблюдатель, неподвижный по отношению к системе О, соответственно как Е и В. Физически E означает силу, действующую на единичный покоящийся заряд в системе 0, а В — силу, действующую на единичный элемент тока, неподвижный в системе О: Е = iE_x + jE_y+ kЕ_z; В = iB_x+ jBy+kB _z Напряженность электрического поля и магнитную индукцию, которые измерил бы наблюдатель, неподвижный по отношению к системе О₁ (т. е. движущийся со средой со скоростью v), обозначим E₁ и В₁. Физически Е ₁означает силу, действующую на единичный покоящийся в системе О ₁заряд; B₁- силу, действующую на единичный
элемент тока, покоящийся в движущейся среде:

E₁=iE_x1+ jE_y1 + kЕ_z1; B₁= iB_x1 + jBy₁ +kB_z1

_{Перейдем от уравнений Максвелла для неподвижных сред к уравнениям Максвелла для движущихся сред. С этой целью частные производные по х, у,z при взя-}

Обратим внимание еще раз на то, что в системе О ₁операции дифференциривания при взятии ротора и дивергенции производятся по координатам х₁, y ₁, z ₁. В системе O ₁, для которой среда неподвижна, выполняется условие непрерывности тангенциальной составляющей напряженности E_tl, тангенциальной составляющей H_t1 и непрерывность нормальных составляющих.D_nl и В_n1. В системе О₁

Из уравнений (22.17) и (22.22) следует, что если в системе О магнитное поле отсутствует (В = 0), но имеется электрическое (Е 0), то в системе О₁ имеется не только электрическое, но и магнитное поле. Из уравнений (22.19) и (22.21) заключаем, что если в системе О отсутствует электрическое поле (Е = 0), но есть магнитное (В ), то в системе О₁ наблюдается не только магнитное, но и электрическое поле. Плотность тока ₁ в системе О₁ создается не только током проводимости , но и током переноса αvρ [см. уравнение (22.18)].

В соответствий с уравнением:(22.25) перемещение; тока с плотностью _х парал­лельно: самому себе с системой О₁ наблюдатель в системе Овоспринимает как воз­никновение объёмного заряда v/с2 _х, , дополнительного к объемной плотности заряда p₁. В соответствии с уравнением (22.28) движение поляризованной среды со скоростью v воспринимается в системе О как появление дополнительной намагниченности, а движение намагниченной среды со скоростью v воспринимается в системе О как возникновение дополнительной поляризации.

Для поля, связанного с системами О и О₁ имеют место следующие инварианты:

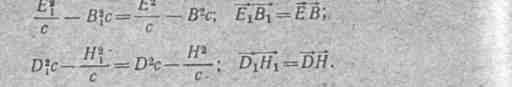
Если скорость движения среды мала по сравнению со скоростью света, то (v²/ c²) 1 и α 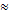1, при этом преобразования Лоренца переходят в преобразования Галилея х ₁= х — vt,y₁ = у, z ₁= z, t₁ = t, а связи между величинами в системах О и О₁, становятся такими:

Вопросы, для самопроверки

1. Дайте определение переменного электромагнитного поля и запишите сово- купность уравнении Максвелла. 2. Покажите, что из первого уравнения Максвелла следует принцип непрерывности полного тока (или закон сохранения заряда), а из второго — принцип непрерывности магнитной индукции. 3. Чем объяснить, что во втором уравнении Максвелла, в отличие от первого, поставлен знак минус? 4. Ка­кие уравнения в интегральной форме соответствуют 1-му и 2-му уравнениям Макс­велла? 5. Прокомментируйте теорему Умова—Пойнтинга для мгновенных значе-

ний величин и для величин в комплексной форме записи. 6. Можно ли утверждать,
что при постоянном токе электромагнитная энергия передается по проводам? 7. Поясните смысл преобразования, осуществляемого с помощью теоремы Остроградского Гаусса. 8. Чем объяснить, что показание вольтметра в переменном электромаг­нитном поле зависит от того, как расположены провода от вольтметра до объекта измерения. 9. Поясните, в силу каких причин ε, у и . Могут оказаться комплекс­ными числами. 10. Какие среды называют анизотропными? 11. Решите задачи 22.2; 22.9;22.11.

 

 

ГЛАВА ДВАДЦАТЬ ТРЕТЬЯ

БЕРЕМЕННОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ В ОДНОРОДНОЙ И ИЗОТРОПНОЙ ПРОВОДЯЩЕЙ СРЕДЕ

§23.1. Уравнения Максаелла для проводящей среды. Рассмотрим особенности распространения электромагнитной волны в прово­дящей среде с проводимостью у и магнитной проницаемостью μ_а.

Обратимся к первому и второму уравнениям Максвелла, записан­ным в комплексной форме для синусоидально изменяющихся во времени Е и Н:

и

 

B проводящей среде даже при очень высоких частотах произведе- ние^: ωε_а много меньше проводимости у. Поэтому с большой степенью точности слагаемым jωε_а Ё в первом уравнении Максвелла для про­изводящих сред можно пренебречь.

В настоящее время наука не располагает точными данными о числовом значении электрической проницаемости ε для металлов. Имеются лишь сведения, что порядок ε для металлов такой же, как и для большинства диэлектриков (т. е. от нескольких единиц до нескольких десятков). В качестве примера возьмем ε для меди, равное 10, и найдем, во сколько раз ток проводимости в ней будет больше тока смещения при ω=10³ и при ω = 10⁸ рад/с. При ω = 10³

 

т. е. рассмотренном числовом примере даже при ω = 10⁸ ток проводимости больше
тока смещения в 6,33- 10⁹ раз. -

Таким образом, первое и второе уравнения Максвелла для проводящей среды приобретают вид:

Уравнение (23.3) является дифференциальным относительно Н, В общем случае, когда Н зависит от всех трех или даже только от двух координат, решение (23.3) довольно сложно. Поэтому ограничимся рассмотрением решения этого уравнения для частных случаев — для плоской и цилиндрической электромагнитных волн.

образом:

§23.2. Плоская электромагнитная волна. В общем случае под плоской электромагнитной волной понимают волну, векторы Е и Н которой расположены в плоскости хоу, перпендикулярной направлению 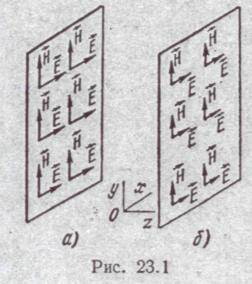распространения волны (ось z)и вменяю­щиеся только в функции координаты zи вре­мени t. В дальнейшем (за исключением §24.8) под плоской волной будем понимать плоскую линейно поляризованную волну, в которой вектор Е направлен вдоль одной, а вектор Н вдоль другой координатной оси плоскости хоу. Плоская линейно поляризованная волна по­казана на рис. 23.1. На рисунке изображены для одного и того же момента времени век­торы Е и Н в двух параллельных плоскостях, перпендикулярных оси z декартовой системы координат. Во всех точках первой плоскости (рис. 23.1, а) напряженность электрического (магнитного) поля одинакова по величине и направлению. Во всех точках второй плоскости (рис. 23.1,6) напряженность электрического (магнитного) поля также одинакова по величине и направлению, но не равна напряженности поля в первой плоскости.

В силу самого определения плоской волны:

В плоской волне Е и Н являются функциями только одной коор­динаты, в рассматриваемом случае функцией только z.

Повернем координатные оси таким образом, чтобы ось у совпала с напряженностью магнитного поля Н. При этом Н=jH, где j —

В этом уравнении (23.5) вместо частной написана обыкновенная производная. Переход от частной производной к обыкновенной для плоской волны является естественным, так как Н— это функция только одной переменной z.

Уравнение (23.5) представляет собой линейное дифференциальное уравнение второго порядка. Его решение записывают следующим образом

где С₁ и С₂ — постоянные интегрирования; это комплексы, которые

определяют из граничных условий; для каждой конкретной задачи это свои постоянные.

Из характеристического уравнения р² =jωγμ_а найдем коэффициент

Найдем напряженность электрического поля с помощью уравнений (23.1) и (23.6). Из (23.1) следует, что Е = 1/γ rotH.

Выражение (23.10') показывает, что напряженность электриче­ского поля в плоской волне при выбранном расположении осей коор­динат направлена вдоль оси х, об этом, свидетельствует присутствие единичного орта оси х (орта i). Таким образом, в плоской электро­магнитной волне между Е и H есть пространственный сдвиг в 90 (Е направлено по оси х, а H — по оси у).

Частное от деления р на у принято называть волновым сопротив­лением:.

где

где

Волновое сопротивление Z_B, измеряемое в омах, зависит от свойств среды (от у и μ_а,) и угловой частоты ω. В соответствии с (23.10') и (23.11) проекция Е на ось х равна:

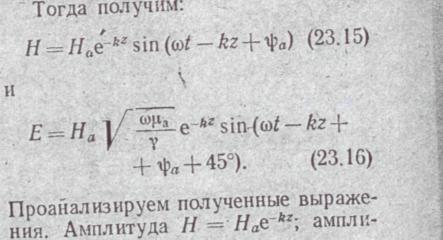
Компоненты падающей волны Е_пад и H_пад дают вектор Пойнтинга П_пзд (рис. 23.2, а), Направленный вдоль положительного направления. оси z. Следовательно, движение энергии падаю­щей волны происходит вдоль положительного направле­ния оси z.

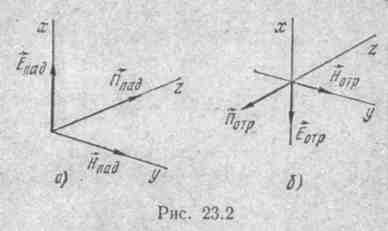Компоненты отраженной отражен-

волны Е_отр и Н_отр дают вектор Пойнтинга П_отр (рис. 23.2, б), направленный вдоль отрицательного направления оси z. Это означает, что отра-

женная волна несет с собой энергию вдоль отрицательного направле­ния оси z.

Волновое сопротивление Z_в можно трактовать как отношение Ё_пад/Н_пад. *. Так как волновое сопротивление является числом ком­плексным [см. формулу (23.12)] и имеет аргумент 45°, то сдвиг во вре­мени между Е_пад и Н_пад для одной и той же точки поля тоже равен 45°.

* Отношение Ё_0ТР к — Н_OTp также равно Z_в

 

проводящей среде, простирающейся теоретически в бесконечность (рис. 23.3). Электромагнитная волна проникает из диэлектрика в проводящую среду и рас­пространяется в ней. Так как среда прости­рается теоретически в бесконечность и па- дающая волна в толще проводящей среды не встречает границы, которая «возмутила» бы ее распространение, то отраженной волны в данном случае не возникает. При наличии только одной падающей волны Н=С2е-рz и Е=ZвС2е-рz

§23.3. Распространение плоской электромагнитной. волны в однодном проводящем полупространстве. Рассмотрим вопрос о распространении плоской электромагнитной волны в однородной

 

 

Постоянную интегрирования С₂ найдем ИЗ граничных условий. Если обозначить напряженность магнитного поля на поверхности поводящей среды через Н_а = Н_ае^i𝜓, то при z=0 С₂ = Н_а. Поэтому c yчетом (23.8) в свою очередь

Чтобы записать выражения для мгновенных значений Н и Е,

необходимо правые части (23.13) и (23.14) умножить на е^iωt и взять мнимые части от получившихся произведений.

туда Е=Н_а а/γ ^-kz .С увеличением zмножитель ^-kz уменьшается

по показательному закону. Следовательно, по мере проникновения электромагнитной волны в проводящую среду амплитуда Е и Н уменьшаются по показательному закону. На рис.23.4 изображены огибающие амплитуд Н, построенные на основе Н_а ^-kz. Мгновенное значение Н и Е определяется аргументом синуса, который в выражении (23.15), например, зависит от z и от ωt. Если принять ωt=сonst, то на графике мгновенных значений Н в функции от z будет получена

 

 

 

Для того чтобы охарактеризовать, насколько быстро уменьшается амплитуда падающей волны по мере проникновения волны в проводя­щую среду, вводят понятие «глубина проникновения».

§23.4. Глубина проникновения и длина полны. Под. глубиной
проникновения понимают расстояние вдоль направления распрост­-
ранения волны (вдоль оси z), на котором амплитуда падающей волны
Е (или H) уменьшается ве= 2,71 раз. Глубину проникновения опре­-
деляют с помощью выражения: е^-k =е^-1. Отсюда следует, что /k = 1
или

= 1/k. (23.17)

Глубина проникновения зависит от свойств проводящей среды (у и μ) и частоты ω.Так, если электромагнитная, волна имеет частоту f=5000 Гц и проникает в проводящую среду, у которой γ= 10⁷ (Ом-м)-¹ и μ= 10³, то*

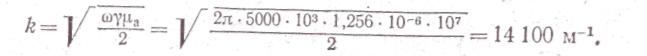
Глубина проникновения — 1/ k 7 10^-5 м, т. е. на расстоянии в 0,007 см амплитуды H и Е снизились в 2,71 раза.

Для рассмотренного числового примера

Под длиной волны λв проводящей среде понимают расстояние вдоль направления распространения волны (вдоль оси z), на котором фаза колебания изменяется на 2л. Длину волны определяют из уравнения λ = 2л. отсюда:

 

 

Иногда пользуются понятием фазовой скорости распространения электромагнитной волны в проводящей среде.

Под фазовой скоростью понимают скорость, с которой надо было бы перемещаться вдоль оси z чтобы колебание имело одну и ту же фазу. Фаза колебания определяется выражением ωt — kz + 𝜓_а

Производная от постоянной есть нуль, поэтому d/dt (ωt-kz+ 𝜓_а) = 0, или

Для рассмотренного числового примера v_фаз = 2π 5000/14100 2,25м/с

-------------------------------------------------

* Полагаем, что μ не зависит от величины Н. Решение, в котором

учтено, что μ является функцией величины Н, дано в [10].

 

§ 23.5. Магнитный поверхностный эффект. В качестве примера распространения плоских электромагнитных волн в проводящей среде рассмотрим поле в стальном листе при прохождении вдоль листа переменного магнитного потока Лист (рис. 23.5) имеет толщину 2а, высоту h ( h a ) и большую протяженность в направлении, перпендикулярном рисунку. Средняя плотность магнитного потока по сечению листа В_ср = Ф_m /2а h.

Задача состоит в определении законов изменения Н и Ё по сечению листа. В силу симметрии напряженность магнитного поля на левой поверхности листа та же, что и на правой поверхности листа. Обозначаем через Н_а и будем полагать известной (в дальнейшем выразим ее через В_ср.)

Так как толщина листа 2а много меньше высоты листа h, то искажающим влиянием краев листа на поле можно в первом приближении пренебречь и считать, что в лист с двух сторон проникает плоская электромагнитная волна. Расположим оси координат декартовой системы в соответствии с рис. 23.5. Примем, как и прежде, Н= jH. Общее решение для Н таково: Н = С₁е ^рz + С₂ е ^–рz.

Из граничных условий найдем постоянные интегрирования. При z= - а, т. е. для точек, находящихся на левой стороне листа,

Напряженность электрического поля

При z = + а напряженность Е направлена вверх (вдоль оси — х)\ при z = — а — вниз (вдоль оси +х, см. рис. 23.5, а). Вектор Пойнтинга направлен к средней плоскости листа (внутрь листа).

Как известно из ч. II учебника, ток, возникающий при прохож­дении по листу переменного магнитного потока, принято называть вихревым. Вектор плотности вихревого тока = уЕ в любой точке

Среднее значение магнитной индукции в листе

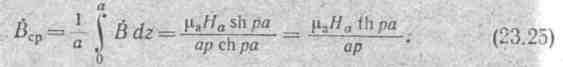
листа коллинеарен с вектором Е в этой же точке. Магнитная индукция в произвольной точке

Если считать, В_ср известной и равной Ф_m /2а h, то из (23.25) можно найти напряженность поля на поверхности листа:

Заметим, что аргумент pa — ka + jka является комплексом и th pa есть гиперболический тангенс от комплексного аргумента; он также является комплексом: