ПРОСТРАНСТВО ЭЛЕМЕНТАРНЫХ ИСХОДОВ W. ОПЕРАЦИИ НАД СОБЫТИЯМИ И ОТНОШЕНИЯ МЕЖДУ СОБЫТИЯМИ

Б.Я.РЯБКО

СБОРНИК ЗАДАЧ

ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ И

ОСНОВАМ ТЕОРИИ МАССОВОГО

ОБСЛУЖИВАНИЯ

Рекомендовано УМО по образованию в области

телекоммуникаций в качестве учебного пособия

для студентов высших учебных заведений, обучающихся

по направлению подготовки бакалавров и магистров

554000 Телекоммуникации

Новосибирск 2010

УДК 519.21

Д.т.н. проф. Рябко Б.Я. Сборник задач по теории вероятностей и основам теории массового обслуживания. 2010, с. 76.

 

Программы технических и экономических предметов, изучаемых в СибГУТИ, и научные исследования, проводимые на кафедрах, наложили определенный отпечаток на преподавание теории вероятностей, теории случайных процессов и теории массового обслуживания. Эти особенности нашли отражение в курсах, читаемых в СибГУТИ и привели к необходимости создания сборника задач, который соответствовал бы учебным программам.

 

 

Кафедра прикладной математики и кибернетики

 

Рисунков – 13, таблиц – 7.

 

 

Рецензенты: В.И.Дубинин, И.Л.Елисеенко

 

Утверждено редакционно-издательским советом СибГУТИ в качестве сборника задач по теории вероятностей и основам теории массового обслуживания.

 

 

ÓСибирский государственный университет

телекоммуникаций и информатики, 2010 г.

 

 

 

ОГЛАВЛЕНИЕ

ПРЕДИСЛОВИЕ.. 4

1 ПРОСТРАНСТВО ЭЛЕМЕНТАРНЫХ ИСХОДОВ W. ОПЕРАЦИИ НАД СОБЫТИЯМИ И ОТНОШЕНИЯ МЕЖДУ СОБЫТИЯМИ.. 5

2 КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ, НАХОЖДЕНИЕ ЧИСЛА ЭЛЕМЕНТОВ В МНОЖЕСТВАХ КОМБИНАТОРНЫМИ МЕТОДАМИ. ГЕОМЕТРИЧЕСКИЕ ВЕРОЯТНОСТИ.. 10

3 ТЕОРЕМЫСЛОЖЕНИЯ И УМНОЖЕНИЯ. НЕЗАВИСИМОСТЬ СОБЫТИЙ. ВЕРОЯТНОСТЬ НАСТУПЛЕНИЯ ХОТЯ БЫОДНОГО СОБЫТИЯ ИЗ НЕСКОЛЬКИХ НЕЗАВИСИМЫХ.. 14

4 ФОРМУЛЫПОЛНОЙ ВЕРОЯТНОСТИ И БАЙЕСА.. 17

5 СХЕМА БЕРНУЛЛИ.. 21

6 ПРИБЛИЖЕННЫЕ ФОРМУЛЫВ СХЕМЕ БЕРНУЛЛИ.. 23

7 ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ... 26

8 МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫИ ИХ ХАРАКТЕРИСТИКИ. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН 35

9 ОДНОРОДНЫЕ ЦЕПИ МАРКОВА (ДИСКРЕТНОЕ ВРЕМЯ) 44

10 МАРКОВСКИЕ ПРОЦЕССЫ... 47

11 ВАЖНЕЙШИЕ ПРОЦЕССЫ, МОДЕЛИРУЮЩИЕ ПОТОКИ СОБЫТИЙ.. 52

12 ПРЕДЕЛЬНЫЙ РЕЖИМ ДЛЯ МАРКОВСКИХ ПРОЦЕССОВ.. 54

13 ВАЖНЕЙШИЕ СИСТЕМЫМАССОВОГО ОБСЛУЖИВАНИЯ, МОДЕЛИРУЕМЫЕ МАРКОВСКИМИ ПРОЦЕССАМИ 59

ОТВЕТЫ... 64

ПРИЛОЖЕНИЕ.. 75

 

ПРЕДИСЛОВИЕ

 

Теория вероятностей и тесно связанные с ней математическая статистика и теория случайных процессов находят самое широкое применение в телекоммуникациях, информатике и экономике. Поэтому теория вероятностей изучается практически на всех факультетах СибГУТИ, хотя, естественно, читаемые разным специальностям курсы отличаются своим содержанием. Сборник задач охватывает темы, изучаемые во всех курсах теории вероятностей, читаемых в СибГУТИ и поэтому может использоваться на всех факультетах.

Данный сборник формировался автором в течение многих лет и базируется на ранее опубликованных изданиях:

1. Рябко Б.Я. Методические указания «Марковские процессы», НЭИС, 1988.

2. Рябко Б.Я., Суздальницкий И.Д. Методические указания и задачи к практическим занятиям по теории вероятностей. НЭИС, 1991.

3. Рябко Б.Я., Суздальницкий И.Д. Методические указания и задачи к практическим занятиям по теории вероятностей; Часть 2: Случайные процессы, НЭИС, 1994.

При этом из двух последних работ в данный сборник включены только разделы, написанные лично автором данного пособия.

 

В заключении я хотел бы выразить благодарность профессору И.Д. Суздальницкому, много лет назад инициировавшему написание данного сборника, и доценту О.А.Ахметову, потратившему много времени и сил на редактирование данного издания.

 

Рябко Б.Я.

 

 

ПРОСТРАНСТВО ЭЛЕМЕНТАРНЫХ ИСХОДОВ W. ОПЕРАЦИИ НАД СОБЫТИЯМИ И ОТНОШЕНИЯ МЕЖДУ СОБЫТИЯМИ

 

В теории вероятностей исследуются случайные события, которые могут происходить в результате проведения некоторых экспериментов (опытов) или испытаний. Под множеством элементарных исходов, связанным с данными экспериментом, понимается множество взаимоисключающих друг друга исходов. Множество элементарных исходов обозначают W, а его элементы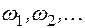

События, которые могут произойти в результате эксперимента представляют в виде подмножеств W и обычно обозначают большими латинскими буквами. Говорят, что некоторое событие А произошло (наступило) при проведении эксперимента, если результат эксперимента – элементарный исход w, принадлежащий подмножеству, соответствующему А.

Среди всех событий выделяют достоверное и невозможное, обозначаемое через W и Æ, соответственно. Достоверное событие происходит всегда при проведении эксперимента, а невозможное – никогда не происходит. Достоверному событию соответствует все W, невозможному – пустое множество.

Суммой событий А и В, обозначаемой A+B, называют событие, которое наступает тогда, когда происходит или событие А, или В, или оба вместе). На языке теории множеств сумме событий соответствует объединение подмножеств. Аналогично определяется сумма нескольких событий: 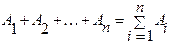происходит тогда, когда наступает хотя бы одно из А_i.

Произведением событий А и В называется событие, обозначаемое А×В, происходящее тогда, когда наступают А и В. Событию А×В соответствует подмножество W, состоящее из элементарных исходов, принадлежащих подмножествам и А и В. Аналогично, событие происходит тогда, когда наступают все . Произведению событий 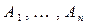соответствует пересечение подмножеств.

Противоположное событие к событию А, обозначаемое , наступает тогда, когда А не происходит. Событие состоит из элементов W, не входящих в А. 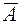называют также отрицанием А или дополнением А.

События А и В несовместимы, если не могут произойти вместе при одном испытании. Подмножества, соответствующие А и В, не имеют общих элементарных исходов.

События попарно несовместны, если любые два из них несовместны.

Попарно несовместные события 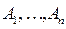образуют полную группу событий, если .

ЗАДАЧИ

1. Монета подбрасывается два раза. Описать пространство элементарных исходов W и события: А – первый раз выпал герб, В – один раз выпал герб, С – выпал хотя бы один раз герб. Будут ли совместны А и В? В и С?

2. Студент выучил к экзамену первые 20 вопросов из 30. На экзамене задают два случайно выбранных вопроса. Надо записать события: А – студенту попались два выученных вопроса, В – студенту попался один выученный вопрос, С – попадается хотя бы один выученный вопрос. Выразите С через А и В. Указание: .

3. Игральная кость подбрасывается два раза. Надо выписать пространство элементарных исходов и события А={первый раз выпало четное число очков}, В – {произведение выпавших очков нечетно}, C –{сумма больше 10}, .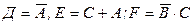

4. Монета подбрасывается до первого выпадения герба. Выписать пространство элементарных исходов и события А={герб выпал при втором подбрасывании}, В={потребовалось не более трех подбрасываний}, С={потребовалось четное число подбрасываний},

5. Образуют ли полную группу следующие группы событий:

а) Опыт – бросание монеты; события:

А₁ – появление герба,

А₂ – появление цифры.

б) Опыт – бросание двух монет; события:

В₁ – появление двух гербов,

В₂ – появление двух цифр.

в) Опыт – два выстрела по мишени, события:

С₁ – ни одного попадания,

С₂ – два попадания.

г) Опыт – два выстрела по мишени, события:

Д₁ – хотя бы одно попадание,

Д₂ – хотя бы один промах.

6. Для социологического исследования случайно выбирается одна семья с тремя детьми. Рассматриваются события: А={первый ребенок мальчик}, D={первый – мальчик, третий – девочка}, C={есть мальчик и девочка}. Надо выписать пространство элементарных исходов W и события А,В,С. Проверить, будут ли совместны А и В, 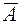и В. Описать словестно и в виде подмножеств W события .

7. В комнате общежития живут четыре студента. Они решили по жребию разыграть два билета в театр. Для этого они приготовили четыре листочка бумаги, два с буквой «Т», два с «Н» и поочередно случайно взяли по одной бумажке. Надо выписать пространство элементарных исходов и события А={билет достался первому и последнему студенту} B={билет достался студенту, который берет листочек третьим}, C={билеты достанутся двум последовательно берущим листочки студентам}. Найдите . Совместны ли А и В? А и С?.

8. Участок электрической цепи имеет вид, изображенный на рисунке. Разрыв цепи, событие А, может произойти вследствие выхода из строя элементов 1,2,3 (соответственно, событий А₁, А₂, А₃). Выразить событие А через А₁, А₂, А₃.

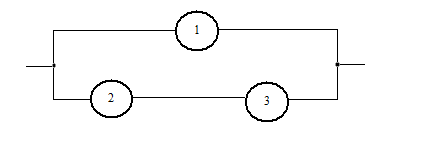
Рисунок 1

 

9. Обозначим через А_i события (i=1,2,3,4) быть исправным для соответствующего элемента электрической цепи. Выразить через А_i событие А, состоящее в том, что по цепи идет ток.

а)

б)

в)

г)

 

Рисунок 2

 

10. Проверяются три прибора. Пусть событие А заключается в том, что хотя бы один из проверяемых приборов бракованный, событие В – все приборы доброкачественные. Что означают события:

1. ?

11. Измеряются две величины. Ошибка измерения первой величины может принимать значения из промежутка [0;5], а второй из промежутка [0;10]. Рассматриваются следующие события: A={ошибка измерения первой величина не превышает 3}; В= {обе ошибки измерений превышают 2}; С= {разница ошибок измерений не превышает 1}. Изобразить графически W, А, В, С, .

12. На отрезке длины 6 наудачу взяты две точки. Рассматриваются следующие события: А={первая точка дальше середины отрезка}; В={обе точки расположены дальше середины отрезка}; С= {расстояние между точками не превышает 2}. Изобразить графически W, А, В, . Совместны ли А и В?

13. В сигнализатор поступают сигналы от двух устройств, причем поступление каждого из сигналов равновозможно в любой момент промежутка времени Т=20 мин. Рассматриваются следующие события:

А={второй сигнал поступил до момента Т/2};

В={оба сигнала поступили после момента Т/4 };

С={моменты прихода сигналов отличаются не более, чем на 5 мин.}.

Изобразить графически А, В, С, 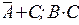. Будут ли совместны А и В? и В? В и С?

14. На круглом экране радиолокатора радиуса 20 см имеется точечное изображение объекта, занимающее положение в пределах экрана. Рассматриваются следующие события:

А ={расстояние от центра до изображения не превышает 10 см};

В ={изображение удалено от центра не менее, чем на 5 см}

С ={расстояние от центра до изображения не меньше 5 см, но не больше 15 см}; Изобразите W, А, В, С, .

15. Проверяется возраст супругов. Предполагая, что возраст супругов может быть от 16 до 150 лет, описать пространство элементарных событий W и следующие события:

А - мужу больше 20 лет;

В - жене больше 20 лет;

С - муж старше жены;

Д - возраст супругов совпадает;

Е - возраст супругов отличается не более, чем на 2 года. Изобразить на плоскости пространство W и события А, В, С, Д, Е.

16. Что означают следующие события:

1. А + Æ

2. А + W

3. А + А

4. А ×Æ

5. А × W

6. А ×А

17. А, В, С - произвольные события. Найти выражения для следующих событий:

а) произошло только А,

б) произошли Аи В, ноне произошло С,

в) произошли все три события,

г) произошло по крайней мере одно из них,

д) произошло по крайней мере два события,

е) произошло одного и только одно событие,

ж) произошли два и только два события,

з) не произошло ни одного события,

и) произошло не более двух событий.

18. Среди студентов, собравшихся на лекцию, наугад выбирают одного. Пусть событие А состоит в том, что выбранный окажется юношей, событие В – выбранный не курит и событие С – выбранный проживает в общежитии.

1. Описать события: .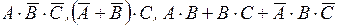

2. При каком условии будет иметь место равенство АВС= В?

3. Когда будут справедливо соотношение ?

19. Равны ли события А и В, если:

1.

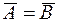
2. А+С=В+С

3.

20. Производится наблюдение за четырьмя однородными объектами. Каждый из них за время наблюдения может быть обнаружен или нет. Рассматриваются события:

А - обнаружен ровно один объект из 4-х,

В -обнаружен хотя бы один объект,

С -обнаружено не менее двух объектов,

Д -обнаружены два объекта,

J - обнаружено равно три объекта,

F -обнаружены все четыре объекта.

Указать, в чем состоят события: а) А+В, б) А В, в) В+С,г) В×С, д) Д+F+E, е) B × F.