Для n-мерной случайной величины  , n>1 функция распределения определяется равенством
, n>1 функция распределения определяется равенством
 (8.1)
(8.1)
Дискретная n-мерная случайная величина  , принимающая значения
, принимающая значения 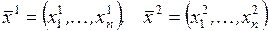 может быть задана набором вероятностей
может быть задана набором вероятностей
 . (8.2)
. (8.2)
В случае двумерной величины эти вероятности удобно представлять в виде таблицы
| x1 / x2 | Y1 | Y2 | … | Yk |
| X1 | P11 | P12 | … | P1k |
| X2 | P21 | P22 | … | P2k |
| … | … | |||
| Xm | Pm1 | Pm2 | … | Pmk |
Непрерывная n-мерная случайная величина может быть задана плотностью распределения
 (8.3)
(8.3)
Функция распределения выражается через плотность следующим образом:
 (8.4)
(8.4)
Вероятность попадания непрерывной случайной величины  в область D равна интегралу от плотности по D.
в область D равна интегралу от плотности по D.
Пусть  – двумерная случайная величина, причем
– двумерная случайная величина, причем 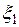 принимает значения
принимает значения  ,
,  – значения
– значения  ,
,  и пусть
и пусть

Тогда для одномерных законов распределения справедливы формулы

 (8.5)
(8.5)
Условный закон распределения случайной величины 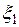 при условии, что
при условии, что  равно некоторому Yj, определяется равенством.
равно некоторому Yj, определяется равенством.
 (8.6)
(8.6)
Для двумерной непрерывной случайной величины  плотность вероятности случайных величин
плотность вероятности случайных величин 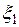 и
и  может быть найдена по формулам
может быть найдена по формулам
 (8.7)
(8.7)
Условная плотность распределения 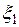 при условии, что
при условии, что 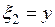 (и
(и  ), определяется равенством
), определяется равенством
 (8.8)
(8.8)
Случайные величины  независимы, если для всех
независимы, если для всех  выполняется равенство
выполняется равенство
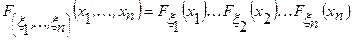 (8.9)
(8.9)
Для дискретных случайных величин это равенство эквивалентно выполнению соотношения
 (8.10)
(8.10)
для непрерывных
 (8.11)
(8.11)
при всех  .
.
Для двумерной случайной величины  ковариация определяется равенством
ковариация определяется равенством
 (8.12)
(8.12)
а коэффициент корреляции равенством
 , (8.13)
, (8.13)
где  - стандартное отклонение x.
- стандартное отклонение x.
Вычислить 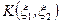 для дискретных случайных величин
для дискретных случайных величин  можно по формулам
можно по формулам
 , (8.14)
, (8.14)
где  - значения
- значения  - значения
- значения 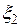 .
.
Для непрерывных  справедлива формула
справедлива формула
 (8.15)
(8.15)
Ковариационная матрица К для n случайных величин  определяется соотношением
определяется соотношением
 ,
,
а корреляционная

Здесь  . Обе эти матрицы симметричны.
. Обе эти матрицы симметричны.
Пусть x и h – случайные величины, связанные соотношением  , где j - неслучайная функция. Если x – дискретная случайная величина, то закон распределения h может быть найден из соотношения
, где j - неслучайная функция. Если x – дискретная случайная величина, то закон распределения h может быть найден из соотношения
 , (8.16)
, (8.16)
где  - множество значений xi, случайной величины x таких, что
- множество значений xi, случайной величины x таких, что  .
.
Если x - непрерывная случайная величина, а j - монотонная функция, то плотность и функция распределения случайной величины  могут быть найдены по формулам
могут быть найдены по формулам
 , (8.17)
, (8.17)
где  - функция, обратная j. В общем область определения
- функция, обратная j. В общем область определения  надо разбивать на участки монотонности и использовать аналогичные формулы.
надо разбивать на участки монотонности и использовать аналогичные формулы.
В том случае, когда  , где
, где  - двумерная величина, справедливы равенства
- двумерная величина, справедливы равенства
 (8.18)
(8.18)
 (8.19)
(8.19)
соответственно, для дискретных и непрерывных  .
.
В важном частном случае  для дискретных случайных величин
для дискретных случайных величин  и
и 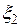 справедливо соотношение
справедливо соотношение
 , (8.20)
, (8.20)
где  значения h; xi; i=1,…,m – значения x. Для непрерывных случайных величин
значения h; xi; i=1,…,m – значения x. Для непрерывных случайных величин
 (8.21)
(8.21)
Плотность вероятности для системы двух нормальных случайных величин  и
и 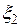 (двумерного нормального распределения) задается равенством
(двумерного нормального распределения) задается равенством
 , (8.22)
, (8.22)
где  - параметры, причем
- параметры, причем

Задача о наилучшем линейном прогнозе
Пусть даны случайные величины  , h, определенные на пространстве элементарных исходов W. Рассмотрим следующую задачу. Даны конкретные значения случайных величин
, h, определенные на пространстве элементарных исходов W. Рассмотрим следующую задачу. Даны конкретные значения случайных величин  , полученные в результате опыта, и требуется предсказать значение случайной величины h. При этом предсказанное значение, которое обозначим через
, полученные в результате опыта, и требуется предсказать значение случайной величины h. При этом предсказанное значение, которое обозначим через  , должно быть линейной функцией
, должно быть линейной функцией 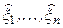 , т.е.
, т.е.  можно представить в виде
можно представить в виде
 , (8.23)
, (8.23)
где  - постоянные величины.
- постоянные величины.
Оценка  также является случайной величиной, и коэффициенты
также является случайной величиной, и коэффициенты  , минимизирующие дисперсию
, минимизирующие дисперсию  (при любых значениях
(при любых значениях 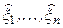 ) могут быть найдены как решение системы уравнений
) могут быть найдены как решение системы уравнений

Причем  (если система уравнений не имеет решения, то можно построить прогноз по части величины
(если система уравнений не имеет решения, то можно построить прогноз по части величины 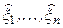 ). В случае n=1, т.е. прогноза h по x решение системы уравнений выписывается явно и
). В случае n=1, т.е. прогноза h по x решение системы уравнений выписывается явно и  может быть представлено в виде
может быть представлено в виде
 (8.24)
(8.24)
ЗАДАЧИ
1. Случайная точка  на плоскости распределена по следующему закону:
на плоскости распределена по следующему закону:
| h / x | ||
| -1 | 0,10 | 0,15 |
| 0,15 | 0,25 | |
| 0,20 | 0,15 |
Найти: а) Законы распределения каждой компоненты x и h.
б) Числовые характеристики для (x, h).
2. Случайные величины x и h являются дискретными и независимыми. Законы их распределения даны в виде таблиц:
| xi | yi | |||||||
| Pi | 2/5 | 1/5 | 2/5 | Pi | 1/2 | 1/6 | 1/3 |
Составить закон их совместного распределения и найти его числовые характеристики.
3. По цели производится три независимых выстрела. Вероятность попадания в цель при каждом выстреле Р=0,7. Случайная величина x есть число попаданий в цель, случайная величина h - число промахов. Составить таблицу распределения системы случайных величин x и h вычислить числовые характеристики.
4. Рассматривается двумерная случайная величина  , где
, где  - оценка на экзамене по математике в первом семестре,
- оценка на экзамене по математике в первом семестре,  - во втором. Из многолетнего опыта известно, что в СибГУТИ ряд распределения таков:
- во втором. Из многолетнего опыта известно, что в СибГУТИ ряд распределения таков:
| x1 / x2 | ||||
| 0,01 | 0,3 | 0,05 | 0,02 | |
| 0,05 | 0,05 | 0,2 | 0,04 | |
| 0,02 | 0,02 | 0,04 | 0,2 |
1. Построить ряд распределения  .
.
2. Найти  .
.
3. Известно, что оценка в первую сессию 5. Предскажите оценку во вторую сессию.
5. Игральную кость подбрасывают два раза. Рассматривают две случайных величины: x1 – число выпадений «единицы», x2 – число выпадений «шестерки». Построить ряд распределения двумерной с.в.  и найти
и найти  .
.
6. Составить закон распределения суммы  и определить ее среднее значение, если
и определить ее среднее значение, если  принимает значения 0, 1, 3 с вероятностями
принимает значения 0, 1, 3 с вероятностями  и h принимает значения 0,1 с вероятностями
и h принимает значения 0,1 с вероятностями  и
и  .
.
7. Из многолетнего опыта известно, что величина стипендии в некотором вузе в первом семестре (x1) и втором (x2) – двумерная величина случайная, задаваемая совместным рядом распределения.
| x2 / x1 | |||
| 0,1 | 0,05 | 0,025 | |
| 0,05 | 0,4 | 0,05 | |
| 0,025 | 0,05 | 0,25 |
Надо: 1. Определить средний размер стипендии, получаемой студентом на первом курсе.
2. Найти коэффициент корреляции.
8. Даны две случайные величины x1 и x2, такие, что  . Найти математическое ожидание и дисперсию случайной величины
. Найти математическое ожидание и дисперсию случайной величины  и
и  .
.
9. Известно, что в некоторой стране рост и вес студента – случайная величина, подчиняющаяся двумерному нормальному распределению, причем средний рост 175 см, средний вес – 70 кг. Матрица ковариации этих двух случайных величин такова:
 .
.
Надо: 1. Найти коэффициент между ростом x1 и весом x2.
2. Написать выражение для плотности совместного распределения x1 и x2.
3. Известно, что рост студента 190 см. Предскажите его вес.
10. Доказать, что

11. Пусть x1 - рост мужчины (мальчика) в возрасте 12, 15, 20 лет. В некоторой стране средние значения этих случайных величин равны 140, 170 и 180 см, соответственно, а матрица ковариации такова:
 .
.
В баскетбольной секции занимаются два 15-летних мальчика, у которых рост в 12 лет был 150 и 155 см, а в 15 – 180 и 182 см. Тренер считает, что уровень игры примерно одинаков. Он может одного из спортсменов рекомендовать в спортивную школу и решил рекомендовать более рослого. Правильно ли он поступил? Указание: Предскажите рост 1-го и 2-го спортсмена в 20 лет.
12. Функция распределения случайных величин x и h определяется по формуле
 .
.
Найти вероятность попадания случайной точки в прямоугольник

13. Определить вероятность попадания точки с координатами (x, y) в область, определяемую неравенством  , если координаты случайной точки (x, y) подчинены закону распределения:
, если координаты случайной точки (x, y) подчинены закону распределения:
 при
при  во всех остальных точках плоскости.
во всех остальных точках плоскости.
14. Плотность распределения системы двух случайных величин x и h заданы функцией

Найти: а) коэффициент а;
б) интегральную функцию;
в) вероятность попадания точки (x, y) в квадрат  ;
;
г) плотности распределения компонент.
15. Орудие стреляет в цель. Начало координат помещено в точку прицеливания. Координаты x, y точки попадания независимы и имеют плотности
 .
.
Какова вероятность попадания в круг радиуса R с центром в начале координат?
16. Двумерная случайная величина имеет плотность распределения
 . Найти функции плотности x и y.
. Найти функции плотности x и y.
17. Система случайных величин (x и h) равномерно распределена внутри круга R;
 .
.
Найти плотности распределения этих случайных величин относительно друг друга. Вычислить ковариацию.
18. Плотность распределения двумерной случайной величины (x и h) имеет вид 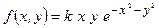 при
при  ,
,  . Найти К.
. Найти К.
19. Плотность вероятностей случайных величин x и h, распределенных на интервалах  имеет вид
имеет вид  . Определить интегральную функцию F(x,y) и числовые характеристики
. Определить интегральную функцию F(x,y) и числовые характеристики 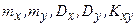 .
.
20. Вероятность первого обнаружения самолета на круглом, радиуса R экране радиолокатора, случайная величина с плотность распределения
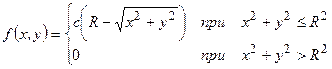 ,
,
где (x,y) – координаты точки обнаружения. Надо найти: а) постоянную с; б) вероятность обнаружения цели в круге радиуса  с центром в начале координат (он совпадает с центром экрана).
с центром в начале координат (он совпадает с центром экрана).
21. Задана плотность  случайной величины x. Найти плотность случайной величины h, если
случайной величины x. Найти плотность случайной величины h, если
1. 
2. 
3. 
4. 
5. 
6. 
Вне указанных промежутков плотность  .
.
22. Случайная величина x распределена по закону
 . Найти закон распределения величины
. Найти закон распределения величины  .
.
23. Случайная величина x распределена по закону
 . Найти закон распределения
. Найти закон распределения  .
.
24. Случайная величина x равномерно распределена на (a,b). Найти плотность распределения вероятностей случайной величины  . Найти
. Найти 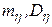 .
.
25. Случайная величина x распределена в интервале (0,¥) с плотностью  . Найти плотность случайной величины
. Найти плотность случайной величины  .
.
27. Системы случайных величин (x и h) распределена нормально  . Найти плотность распределения (r, j), если
. Найти плотность распределения (r, j), если  .
.
28. Случайная величина h зависит от x так, что  , где x подчиняется экспоненциальному закону распределения
, где x подчиняется экспоненциальному закону распределения  при
при 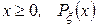 =0 при x<0. Найти математическое ожидание и дисперсию x и y.
=0 при x<0. Найти математическое ожидание и дисперсию x и y.
29. Индикатор кругового обзора навигационной станции представляет собой круг радиуса R. Отраженный от ориентира сигнал с равной вероятностью может появиться в виде пятна в любой точке этого круга. Определить математическое ожидание и дисперсию расстояния центра пятна от центра круга.
30. Система случайных величин подчинена нормальному закону
 .
.
Определить математическое ожидание случайной величины  .
.
31. Брак изделий вызывается двумя причинами: нарушением размеров и низким качеством материала. Плотности вероятностей брака от этих причин соответственно равны
 ,
,
где x и y (x>0, y>0) – процент бракованных деталей вследствие каждой из этих причин. Определить вероятности бракованных деталей вследствие обеих причин и средний процент бракованных деталей.
32. Найти плотность распределения суммы x+y, если
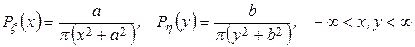 .
.
33. Найти распределение суммы двух равномерно распределенных на интервале (-1; 1) независимых случайных величин.
34. Две независимые случайные величины x и h имеют плотности распределения  .
.
Найти плотность распределения произведения x y.
35. Две независимые случайные величины x и h равномерно распределены на интервале (0;1). Найти вероятность того, что их произведение не превосходит  .
.