ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Рассмотрим пространство элементарных исходов W некоторого испытания. Функция x, определенная на элементах W и ставящая каждому элементарному исходу w некоторое число , называется случайной величиной. Функция распределения случайной величины x, определяется равенством

(7.1)

где х - действительное число (предполагается, что вероятность, стоящая справа в (7.1) определена при всех х). При решении задач часто используются следующие свойства функции распределения:

(7.2)

(при а < b). Полезны также следующие равенства:

(7.3)

Случайная величина x называется дискретной если она принимает конечное или счетное число значений . Дискретная случайная величина может быть задана рядом распределения, который можно представить в виде таблицы

Значения	x₁	x₂	…
Вероятности	P₁	P₂	…

Для дискретной случайной величины выполняется равенство

(7.4)

Случайная величина x называется непрерывной, если существует неотрицательная функция , удовлетворяющая при всех х равенству

(7.5)

называется плотностью вероятности. Она обладает следующими свойствами:

(7.6)

(7.7)

(7.8)

Для непрерывной случайной величины x и числа квантиль порядка Q определяется, как число , удовлетворяющее уравнению

(7.9)

Для дискретной случайной величины x, принимающей значения с вероятностями Р₁, Р₂,... математическое ожидание x, определяется равенством

(7.10)

Для непрерывной случайной величины x, с плотностью распределения математическое ожидание определяется равенством

(7.11)

Дисперсия случайной величины x определяется равенством

(7.12)

справедливо также равенство

, (7.13)

из которого следуют формулы, удобные для вычисления дисперсии дискретных и непрерывных случайных величин:

(7.14)

(7.15)

Стандартное (или среднее квадратичное) отклонение случайной величины x определяется равенством

(7.16)

ВАЖНЕЙШИЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Биноминальное распределение. Случайная величина принимает значения 0, 1, 2, …, n, причем

, (7.17)

где – параметр, – число сочетаний из n по k.

Справедливы равенства

(7.18)

Распределение Пуассона. Случайная величина принимает значения 0, 1, 2,…,

, (7.19)

где - параметр. Для распределения Пуассона

(7.20)

Геометрическое распределение. Случайная величина x принимает значения 1, 2, 3,… с вероятностью

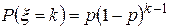, (7.21)

где 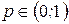- параметр, k=1, 2, …. Для него

(7.22)

Равномерное распределение. Плотность и функция распределения задаются на отрезке [a, b] равенствами.

(7.23)

(7.24)

где - параметры, a < b. Для равномерного распределения

(7.25)

Показательное или экспоненциальное распределение. Плотность и функция распределения таковы:

(7.26)

, (7.27)

где - параметр. Для показательного распределения

(7.28)

Нормальное распределение с параметрами a, s.

Плотность распределения, математическое ожидание и дисперсия даются равенствами:

(7.29)

(7.30)

а функция распределения может быть получена по (7.5). При a=0 и s =1 нормальное распределение называется стандартным.

ЗАДАЧИ

а) Дискретные случайные величины

1. Измерительный комплекс состоит из трех одинаковых приборов, отказы которых происходят независимо друг от друга. Вероятность отказа прибора в течение суток 0,2. Рассматривается случайная величина – число отказавших приборов. Построить ее ряд распределения, найти функцию распределения и построить ее график. Вычислить математическое ожидание и дисперсию.

2. Стрелок производит два выстрела по мишени. Вероятность попадания при каждом выстреле 0,4. За каждое попадание стрелку засчитывается 5 очков. Построить ряд распределения числа заработанных очков.

3. Рабочий обслуживает два станка. Вероятность того, что в течение часа станок потребует внимания рабочего, равна для первого станка 0,8, для второго - 0,9. Найти закон распределения для числа станков, которые потребуют внимания рабочего в течение часа и вычислить среднее число таких станков.

4.Стрелок, имеющий 4 патрона, ведет стрельбу по мишени до первого попадания. Вероятность попадания при каждом выстреле 0,6. Построить ряд распределения количества оставшихся неизрасходованными патронов. Найти интегральную функцию распределения.

5. В семье 4 ребенка. Рассматривается случайная величина x - число мальчиков. Построить ряд распределения и функцию распределения этой случайной величины, считая, что вероятности рождения мальчика и девочки одинаковы.

6. В блоке используются четыре конденсатора двух типов, по два каждого типа. Вероятность отказа в течение гарантийного срока для первого типа равна 0,1, для второго - 0,3. Составить закон распределения числа отказов всех четырех конденсаторов. Найти интегральную функцию распределения, математическое ожидание и дисперсию.

7. В приборе три блока, стоимость каждого 10 руб., стоимость всего прибора - 40 руб. Если в течение года работы выйдет из строя один блок, то его заменяют, если выйдет из строя более одного блока, то заменяют прибор. Известно, что блоки выходят из строя независимо друг от друга, а вероятность выхода из строя одного блока в течение года 0,2. Рассматривается случайная величина - годовые расходы на эксплуатацию прибора. Построить ее ряд распределения и найти среднюю величину расходов.

8. В партии из шести кинескопов три высшего качества. Кинескопы берут по одному и проверяют до тех пор, пока не найдут кинескоп высшего качества. Рассматривается случайная величина - число проверенных кинескопов. Построить ее ряд распределения и вычислить математическое ожидание и дисперсию. Найти функцию распределения.

9. Студент знает 15 вопросов из 20. Экзаменатор задает ему 3 вопроса. Рассматривается случайная величина – число известных вопросов среди заданных. Построить ее ряд распределения, найти функцию распределения, математическое ожидание и дисперсию.

10. В партии из пяти изделий содержится два бракованных. Для проверки контролер берет наугад одно изделие из партии и проверяет его качество. Если оно окажется бракованным, дальнейшие испытания прекращаются, а партия задерживается. Если изделие окажется стандартным, то контролер берет следующее изделие и т.д. Рассматривается случайная величина—количество проверенных изделий. Найти её ряд распределения, функцию распределения, вычислить математическое ожидание и дисперсию. Какова вероятность того, что придется проверять больше двух изделий?

11. Вероятность выиграть по одному билету лотереи «Спринт» равна 0,2; один билет стоит 1 рубль. Некто решил покупать билеты до тех пор, пока один не выиграет (либо пока кончатся деньги). Найти ряд распределения случайной величины - число купленных билетов, если известно, что у этого человека сначала было четыре рубля. Найти среднее значение этой случайной величины. Какова вероятность того, что будет куплено больше двух билетов?

12. Станок-автомат в месяц изготавливает 10000 изделий, причем в среднем на таких станках 90% выпускаемых изделий первого сорта. Если на станке в месяц выпускают больше 9060 изделий первого сорта, то наладчики получают премию в 50 руб., если первосортных изделий от 9000 до 9060, то премия 20 рублей, если же первосортных меньше 9000, то премии нет. Построить ряд распределения случайной величины «размер премии» в случае, когда наладчики работают «средне».

13. В некотором городе среди студентов 20% близоруких. Сколько в среднем будет близоруких среди двухсот случайно отобранных студентов?

14. Известно, что число аварий в год на некотором предприятии подчиняется распределению Пуассона с показателем А= 1,5 (год^-1). Сколько в среднем происходит аварий в год? Какова вероятность того, что в течение года не будет аварий?

15. Для некоторого баскетболиста вероятность попадания в корзину при броске из центра площадки равна 0,2. Он решил бросать мяч до первого попадания. Сколько в среднем бросков потребуется этому спортсмену? Какова вероятность того, что потребуется три броска? Не более трех? Указание: Используйте геометрическое распределение.

16. Дана функция распределения дискретной случайной величины. Построить для неё ряд распределения.

Рисунок 4

17. Вероятность передать без искажений фотоснимок по некоторой линии связи равна 0,7. В случае искажения снимок передается заново, и так до тех пор, пока он не будет передан без искажений. Какова вероятность того, что снимок потребуется передавать более трех раз? Каково среднее число передач одного снимка?

б) Непрерывные случайные величины

1. Дана плотность непрерывной случайной величины (с.в.).

Надо:

а) используя свойства плотности распределения, определить неизвестный параметр с;

б) найти функцию распределения F(x) с.в. x;

в) построить графики функций Р(х), F(x);

г) вычислить математическое ожидание М x и дисперсию D x,

д) найти вероятности

2. Сделать то же, что в первой задаче для плотности .

3. То же, что в первой задаче для плотности .

4. То же, что в задаче №1 для плотности .

5. Найти математическое ожидание и дисперсию случайной величины, заданной функцией распределения

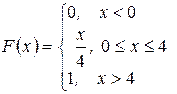
6. Случайная величина задана функцией распределения

Найти с, плотность распределения, математическое ожидание.

7. Годовое потребление угля некоторым предприятием зависит от климатических условий года и является с.в. Из многолетних наблюдений известно, что эта с.в. подчиняется нормальному закону распределения со средним, равным 300 тонн, и стандартным отклонением, равным 5 тонн. В плановом отделе этого предприятия решили, что если запасать 310 тонн угля, то с вероятностью 0,99 этого запаса хватит на год. Правильно ли вычислили вероятность? Если неправильно, то определите, сколько угля надо запасать для того, чтобы с вероятностью 0,99 его хватило на год.

8. Рост юноши в некоторой стране подчиняется нормальному распределению со средним 180 см стандартным отклонением 10 см. В этой стране призывника берут в гвардию, если его рост не меньше 200 см. Какова доля призывников, попадающих в гвардию? Как надо изменить призывную инструкцию для того, что в гвардию призывать 10% новобранцев?

9. Из многолетнего опыта известно, что стоимость списываемого в течение года оборудования на некотором предприятии является случайной величиной, подчиняющейся нормальному распределению со средним 1200 руб. и стандартным отклонением 200 руб. (в том случае, когда при списывании оборудования не происходит нарушений). В вышестоящей организации составлена инструкция, согласно которой на предприятие посылается ревизор, если стоимость списанного оборудования больше 1500 рублей. Какова вероятность послать ревизора на предприятие, на котором при списывании оборудования не происходит нарушений? Как надо составить инструкцию для того, чтобы эта вероятность была равна 0,05?

10. Расход бензина исправного автобуса определенной марки (на 100 км пути) является случайной величиной, подчиняющейся нормальному распределению со средним, равным 15 кг, и стандартным отклонением, равным 2 кг. На некоторой автобазе составлена инструкция, согласно которой автобус отправляется в ремонт, если при испытании он расходует более 20 кг бензина на 100 км пути. Найти вероятность отправки в ремонт исправного автобуса. Как надо составить инструкцию для того, чтобы эта вероятность была равна 0,01?

11. Время между прибытием кораблей в порт - случайная величина, подчиняющаяся экспоненциальному распределению, причем в среднем оно равно 10 часам. Сегодня в 8.00 пришел корабль. Какова вероятность того, что до 24.00 больше не будет кораблей?

12. Случайная величина x имеет нормальное распределение с параметрами а = 1,5 и s = 10. Для этой случайной величины необходимо:

1. Написать выражения для плотности и функции распределения и построить их

графики.

2. Найти математическое ожидание и дисперсию.

3. Найти квантиль порядка 0,96 и медиану.

4. Провести интерпретацию квантиля и медианы на графиках плотности и функции

распределения.

13. Случайная величина x имеет равномерное распределение на промежутке [-2;4]. Для этой случайной величины необходимо:

1. Написать выражения для плотности и функции распределения и построить их

графики.

2. Найти математическое ожидание и дисперсию.

3. Найти квантиль порядка 0,98 и медиану.

4. Провести интерпретацию квантиля и медианы на графиках плотности и

функции распределения.

14. Диаметр вала является случайной величиной, имеющей равномерное распределение на промежутке 98 -- 102 см. Диаметр отверстия равен 101 см. Найти математическое ожидание и среднее квадратичное отклонение зазора между валом и отверстием, а также вероятность того, что вал войдет в отверстие.

15. Шарики для подшипников считаются годными, если проходят через отверстие диаметром 10, 1 мм и не проходят через отверстие диаметром 9,9 мм. Технология изготовления шариков такова, что диаметр шарика можно считать случайной величиной, имеющей нормальное распределение со средним значением 10 мм и стандартным отклонением 0,1. Найти вероятность браковки наугад взятого шарика. Каким должно быть стандартное отклонение, чтобы вероятность браковки шарика была равна 0,005?

16. Известно, что вес деталей подчиняется нормальному закону распределения со средним 10 кг и стандартным отклонением 250 г. Найти вероятность того, что вес случайно отобранной детали будет

а) превышать среднее значение детали не более чем на 500 г;

б) отклоняться от среднего значения не более, чем на 500 г.

17. Завод выпускает детали, номинальная длина которых равна 20 см. Полагая величину ошибки размера деталей случайной, подчиняющейся нормальному закону распределения с нулевым средним, определить, каким должно быть среднее квадратичное отклонение этой ошибки, чтобы длина наугад взятой детали с вероятностью 0,95 была не менее 19,98 см, но не более 20,02.

18. Грузоподъемность самолета составляет (не считая веса пилота) 360 кг. Допустим, что вес пассажира -- случайная величина, распределенная по нормальному закону со средним весом 75 кг и стандартным отклонением 15 кг. Определить вероятность того, что самолет будет перегружен, если он берет на борт четырех пассажиров.

19. Известно, что время службы телевизора до первой поломки подчиняется экспоненциальному (показательному) распределению, причем, в среднем оно составляет 0,5 года. Гарантийный срок работы телевизора 1 год. Какова вероятность того, что в течение гарантийного срока поломок не будет? Какой гарантийный срок надо установить для того, чтобы доля телевизоров, поступающих в гарантийный ремонт, была бы 20%?

20. Известно, что время работы прибора (до замены) подчиняется экспоненциальному распределению со средним 2 года. Найти вероятность того, что прибор проработает до замены не менее 1,5 года.

21. Функция распределения непрерывной случайной величины x задана выражением

Найти коэффициент «а», вероятность попадания случайной величины в интервал (1,2) и плотность распределения вероятностей. Построить графики функций.

22. Интегральная функция распределения случайной величины x имеет вид

Известно, что для рассматриваемой случайной величины функция распределения непрерывна. Надо найти значения А и В. Чему равна вероятность попадания случайной величины в интервал ? Найти плотность распределения вероятностей этой случайной величины.