ВАЖНЕЙШИЕ СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ, МОДЕЛИРУЕМЫЕ МАРКОВСКИМИ ПРОЦЕССАМИ

 

Рассмотрим систему, состоящую из s одинаковых обслуживающих приборов (s > 1). Известно, что поток требований пуассоновский (простейший) с параметром l, а время обслуживания заявки одним прибором подчиняется экспоненциальному распределению с параметром m. Рассмотрим сначала систему с неограниченной очередью. Режим ее работы описывается следующим образом: в том случае, когда в системе есть свободные (не занятые обслуживанием) приборы, вновь поступившее требование немедленно начинает обслуживаться. Если же все приборы заняты, то поступающие требования образуют очередь. Как только один из приборов освобождается, требование, находящееся в голове очереди поступает к нему на обслуживание.

Обозначим через вероятность того, что в момент времени t в системе находится n требований (при все требования обслуживаются, при n > s только n требований обслуживаются, (n–s) находятся в очереди). Для этих вероятностей справедлива следующая система дифференциальных уравнений

(13.1)

(13.2)
(13.3)

В том случае, когда , у рассматриваемой системы существует предельный, стационарный режим, для предельных вероятностей которого справедливы равенства:

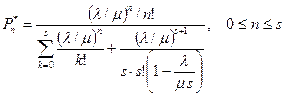(13.4)

 

(13.5)

Величина часто называется суммарной загрузкой системы или полным коэффициентом системы. Величина m – интенсивность обслуживания одного прибора - суммарная интенсивность обслуживания.

Для системы массового обслуживания представляют практический интерес следующие характеристики:

1) Среднее число требований в системе

(13.6)

2) Среднее число требований в очереди

(13.7)

3) Среднее число обслуживаемых требований

(13.8)

4) Среднее число свободных приборов

(13.9)

Для рассматриваемой системы с s приборами и суммарной загрузкой справедливы соотношения:

, (13.10)

где 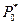определено в (11.4). Кроме того, для этой системы среднее время ожидания в очереди и среднее время пребывания в системе обслуживания можно вычислить по формулам:

(13.11)

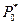( дано в (13.4)).

Другой важный случай – система массового обслуживания с отказами. Рассмотрим систему с s () обслуживающими приборами. Пусть, как и раньше, на вход системы поступает пуассоновский поток требований с параметром l, время обслуживания заявки одним прибором подчиняется экспоненциальному распределению с параметром m. Если обозначить через 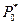, n=0,1,…, вероятность того, что в момент t в системе находятся n требований, то для этих вероятностей справедливы уравнения

(13.12)

(t)

У этой системы обслуживания существуют стационарный режим и предельные вероятности определяются формулами Эрланга:

(13.13)

Для системы с отказами представляют интерес среднее число обслуживаемых требований и среднее число свободных приборов . Эти величины могут быть найдены по формулам (13.8), (13.9) и (13.13).

Рассмотрим теперь случай, когда общее число требований, участвующее в процессе массового обслуживания, ограничено и равно некоторому m (в двух рассматриваемых ранее задачах это число было потенциально неограниченно, бесконечно). Пусть по прежнему s - число приборов, а m - интенсивность обслуживания одним прибором, т.е. другими словами, время обслуживания прибором одного требования подчиняется экспоненциальному распределению с параметром m. Если требование поступает в систему, когда там есть свободные приборы, то оно немедленно поступает к одному из приборов, иначе ждет своей очереди.

Обозначим через вероятность того, что в момент t нуждаются в обслуживании k требований. Типичный пример - s рабочих обслуживает m станков-автоматов. Здесь - вероятность того, что в момент t k станков требуют внимания рабочих. Для этой системы при любых m и l, существует стационарный режим работы и предельные вероятности даются формулами (13.14):

(13.14)

ЗАДАЧИ

1. Рассматривается работа автоматической телефонной станции (АТС), рассчитанной на одновременное обслуживание 20 абонентов (двадцатиканальная СМО). Известно, что вызов на АТС поступает, в среднем, один раз в 6 секунд. Каждый разговор длится в среднем 2 минуты. Если абонент застает АТС занятой, то он получает отказ. Если абонент застает свободным хотя бы один канал, то он соединяется с нужным ему номером. Определить: 1) вероятность того, что абонент, вызывая АТС, не застает ее занятой; 2) определить среднее число занятых каналов.

Решение. АТС можно рассматривать как систему массового обслуживания с отказами. Здесь s=20; (1/сек); . (Это следует из формулы для среднего экспоненциального распределения (11.4)).

Вероятность того, что система не будет занята (Р_св) можно вычислить так:

Используя таблицу для распределения Пуассона или калькулятор, можно получить Р_св =0,841.

Среднее число занятых каналов равно среднему числу обслуживаемых абонентов и находится по формуле (13.8)

 

 

Вычисляя, находим, что .

2. На автозаправочной станции (АТС) имеется 4 колонки. Заправка одной машины длится в среднем 3 минуты. В среднем на АТС каждую минуту прибывает машина, нуждающаяся в заправке. Если колонки заняты, то прибывающие машины встают в очередь. Число мест в очереди практически не ограничено. Определить среднее время, проходящее с момента прибытия машины на заправку, до момента ее заправки и среднее число обслуживаемых на АТС машин.

Указание. Работа АТС может рассматриваться как работа системы массового обслуживания с неограниченной очередью. У этой системы существует стационарный режим (проверьте!). Здесь s=4, l= 1 (1/мин.), m= 1/3 (1/мин.).

3. В общежитии вечером работают два буфета, расположенные рядом так, что очередь в эти буфеты общая. Обслуживание одного покупателя длится, в среднем, 2 минуты. В среднем в буфеты прибывает 2 человека в 3 минуты. Определить среднее время, которое затрачивает покупатель от момента прихода в буфет до приобретения покупки. Какова вероятность того, что покупателю не придется стоять в очереди?

4. В учреждении три телефона-автомата, расположенных в вестибюле, в одном месте. Известно, что средняя продолжительность телефонного разговора 3 минуты, а поток людей, желающих поговорить по телефону, можно считать простейшим с параметром l=0,5 (1/мин.). Чему равно среднее время, которое люди проводят в очереди у автоматов? Какова вероятность того, что человек, пришедший позвонить, застанет свободным все три автомата?

5. Предположим, что в условиях предыдущей задачи, телефоны-автоматы в учреждении переставили в разные части здания, так, что очередь стала у каждого автомата своя. Считая, что к каждому автомату приходит третья часть всех желающих, определить, чему равно среднее время ожидания в очереди. Сравните эту величину в задачах 5 и 4 и объясните качественно причину различий.

6. В читальном зале института 10 одинаковых методических пособий для заочников по теории случайных процессов. В период сессии заочники приходят за этими пособиями в среднем один человек в двадцать минут и работают с этим пособием в среднем по два часа. Если студент не застает пособия в читальном зале, то он уходит. Найти вероятность того, что студент, обратившийся за пособием в читальный зал, сможет его получить.

7. В парикмахерской 2 мастера. В среднем за час в парикмахерскую приходит 4 клиента, а время обслуживания одного посетителя занимает, в среднем, 20 минут. Если оба мастера заняты, то прибывший клиент ждет обслуживания. Сколько, в среднем, парикмахеров будут свободны?

8. В грузовом порту три причала для судов. Судно, прибывающее в порт, сразу встает под разгрузку и погрузку к свободному причалу, если же такого нет, то встает в очередь и ждет освобождения одного из причалов. Поток прибывающих судов можно считать простейшим с параметром l= 1,5 (штук/сутки). Время разгрузки и погрузки (суммарное) у причала, подчиняется экспоненциальному (или показательному) распределению m=0,8. Определить, сколько, в среднем, кораблей находится у причала?

9. Рабочий обслуживает два станка-автомата. Среднее время между поломками одного станка равно 4 часам, среднее время устранения неисправности равно 3 часам. Определить среднее время простоя станков и среднее время простаивающих без ремонта станков.

Указание. Первая величина равна , вторая , где определены в (13.14).

10. Группа из трех рыболовных траулеров обслуживается одной плавучей базой. Траулеры сдают пойманную рыбу на базу. Среднее время плавания траулера равно четырем суткам. Среднее время обслуживания траулера - сутки. Определить среднее время ожидания разгрузки траулером, если время плавания и время разгрузки – случайные величины, подчиняющиеся экспоненциальному распределению.

11. Доказать, что для системы обслуживания с s приборами и неограниченной очередью для среднего числа требований в системе , среднего числа требований в очереди ,0 среднего числа обслуживаемых требований и среднего числа свободных приборов справедливы соотношения:

Указание: Воспользоваться определениями (13.6) – (13.9).

12. Составить граф состояний для системы с отказами и по этому графу получить систему уравнений (13.12). (Подробное описание системы дано перед этими уравнениями). Получить из этих уравнений стационарные вероятности (13.13).

 

ОТВЕТЫ

1. W={ГГ, ГЦ, ЦГ,ЦЦ}, A={ГГ,ГЦ}, А и В совместны.

2. А={(i,j), i,j=1,…,20, i ¹ j; C=A+B.

3. W={(i,j), i=1,…,6, j=1,…,6}, A={i, j); i =2,4,6; j=1,…,6.

4. W={Г, ЦГ, ЦЦГ,…}, A={ЦГ}, B={Г, ЦГ, ЦЦГ}.

5. а) да; б) нет; в) нет; г) да.

6. А={МММ, ММД, МДМ, МДД}, B={ММД, МДД}.

7. W={ТТНН, ТНТН, ТННТ, ННТТ, НТНТ, НТТН}, A={ТННТ}, B={ННТТ, ТНТН, НТТН}.

8. A= A₁A₂+ A₁A₃

9. a) A= A₁A₂+ A₃A₄ б) A= (A₁ + A₃) (A₄ + A₂)

в) A= A₁A₂ (A₃ +A₄) г) A= A₁ (A₂+ A₃ +A₄)

10. А +В= W, А × В=Æ, Æ, .

11.

 

12.

14.

16. А + Æ=А, А + W,= W, А + А =А, А × Æ=Æ, А ×W= A, A× A=A.

17. а) б) в) АВС г) А+В+С д) АВ+ВС+СА

18. – курящий юноша, не проживающий в общежитии.

19. 1 – да, 2 – нет, 3 – нет.

20. А+В=В, АВ= А, В+С=В, В × С= С, Д+E+F=C, B × F= F.

1. 1/90. 2. 0. 3. 12/35. 4. 0,75. 5. 2/9. 6. 3/8. 7. 0.032.

8. 14/63. 9. 1/8. 10. А и В совместимы.

; .

11. А и В несовместны. ;

12.

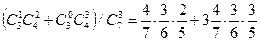
13. А и В несовместны. ;

14. 0,0175; 15. а) 0,4; б) 0,6; в) 30/91.

16. а) 1/336; б) 1/70; 17. 1/18; 1/90.

18. 4/9. 19. .

20. (12 ×8 ×4)(52 ×51×50) (порядок извлечения не учитывается).

21. 1/1296 22. 99/455. 23. . 24. 0,3

25. а) 0,6 б) 0,3 в) 0,9. 26. .

27. Р(А)=2/5, Р(В)=1/5; А и В совместны.

28. 2/3. 29. ; А и В совместны, А и С несовместны.

30. 31. . 32. 0,225.

33. 5/9. 34. 0,01849. 36. 2/p. 37. 1/3 +2/9 ln 2 » 0,487.

38. 0,9025.

 

1. Р(А)= Р(В)= 1/2; зависимы.

2. ; ; зависимы.

3. ; зависимы.

4. Зависимы. 5. ; .

6. 1/3960. 7.

8.

9. 0,42 10. 0,72. 11. 0,1352. 12. 0,224.

13. 0,9 × 0,8 ×0,95 +0,1 ×0,8 ×0,95 + 0,9 × 0,2 ×0,95+ 0,9 ×0,8 ×0,05= 0,967.

14. 0,64. 15. 0,42. 16.

17. 0,424 22.

23. 24. 3/8

25. . 26. 0,988.

27. 21/22. 28. 12/125. 29. 0,992. 30. 0,88.

31. 0,58 32. 0,41 33. 0,76 34. 0,6

 

1. 0,38 2. 0,03 3. 0,964 4. 0,857

5.

6. 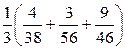7.

8. 9. 0,12

10.

11.

12.

13.

14. 387/640, 175/387. 15. 0,225; 1/9. 16. 0,68

17.

18. 6/7 19. 0,07 20. 6/11 21. 0,19; 80/99.

22. 0,8 23. 71/90 24. 0,83; 14/83.

25. 0,74; 18/14 26. 2,16% 27. 13/132.

 

1. 0,0595; 0,0705 2. 0,317; 0,683. 3. 0,0256; 0,9728.

4. а) 0,254 б) 0,5506 5. 0,2048; 0,058; 0,95. 6. 0,92

7. а) 0,0512 б) 0,256 в) 0,9933

8. а) 0,246 б) 0,9011 9. .

10. а) второе; б) первое; в) второе. 11. 0,875; 7.

12. 0,001 13. 2; . 14. 0,36.

1. 0, 047; 0,066 2. 0,1; 0,9 3. 0,841; 0,994.

4. 0,159; 0,3085 5. 128 6. а) 0,5 б) 0,9772 в) 0,8664 7. 0,38; 388.

9. 0,47 10. 0,27; 0,3233 11. 0,1924 12. 13. 0,18

14. 0,2; 0,71; 0,082 15. 0,55 16. 0,184; 0,63; 0,37.