Прежде, чем рассматривать вопросы проектирования (конструирования) рулевого управления, целесообразно определиться с нагрузочным режимом элементов рулевого управления, т.е. познакомиться с тем, что собой представляет сопротивление повороту управляемых колес и как определить его величину.
Момент, препятствующий повороту управляемого колеса (МСП), складывается из:
– стабилизирующего момента (М3);
– момента сил сопротивления качению колеса относительно оси шкворня (М2)
– момента силы трения скольжения шины по опорной поверхности относительно оси шкворня (М1).
Таким образом: МСП = М1 + М2 + М3.
Момент силы сопротивления качению колеса определяется по выражению:
М1 = G1 f a,
где G1 – нагрузка на ось; f – коэффициент сопротивления качению; а – плечо обкатки (см. рис. 3).
Рис. 3. Расчетная схема определения момента сопротивления качению колеса.
Момент сил трения шины по опорной поверхности определяется по выражению:
,
где: х – плечо момента М2;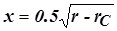 
, где: r – свободный радиус колеса;
rC – статический радиус колеса;
j – коэффициент сцепления; принимают j =0,9
Стабилизирующий момент (момент стабилизации колеса для прямолинейного движения) можно определить по выражению:
, где:
– acp и a2cp — средние углы поворота внутреннего и наружного колес;
– l и g — углы наклона оси шкворня (поперечный и продольный).
Сопротивление повороту управляемых колес определяется при повороте колес на месте на сухой шероховатой поверхности.
Для практических расчетов удобно привести момент сопротивления (МСП) повороту управляемого колеса к валу сошки (МС):
,
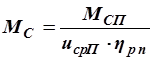где: uср П – силовое передаточное число рулевого привода;
hр п – КПД рулевого привода.
Рассмотрим схему рулевого привода (рис. 4).
Силовое передаточное число рулевого привода, соответствующее началу поворота из правого крайнего положения в левое, находится из выражения:
,
где: Мсп – момент сопротивления повороту управляемых колес;
Мс – момент на валу сошки.
По схеме рулевого привода на рис. 4-а, для крайнего правого положения трапеции величина МС определится из выражения:
.
Тогда: 
,
где: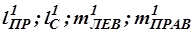 
– активные длины: поворотного рычага, сошки, левого и правого рычагов.
Рис. 4. Схема рулевого привода с неразрезной (а) и разрезной (б) трапецией:
1 – сошка; 2 и 4 – продольная и поперечная рулевые тяги; 3, 5, 6, 8. – рычаги: поворотного кулака (цапфы), рулевой трапеции, подвески, маятниковый (соответственно); 7 – боковая тяга рулевой трапеции; 9 и 10 – шарниры рулевой трапеции.
КПД рулевого управления определяется выражением:
,
где: 
– кпд рулевого привода,
– кпд рулевого механизма.
Величина оценивает потери на трение в шарнирах тяги и шкворневых узлах управляемых колес. Эти потери составляют, соответственно, (10…15)% и (40…50)% от общих потерь в рулевом управлении.
Величина прямого КПД рулевого управления (при передаче усилия от рулевого колеса к управляемым колесам) в среднем составляет (0,67…0,82), а обратного – (0,58…0,63). Значение обратного кпд должно быть выше предела обратимости, но как можно ближе к нему. Первое – необходимо для сохранения стабилизации управляемых колес и «чувства дороги», но, при этом, обратный удар (поворачивающий момент, вызванный наездом колеса на неровность дороги) должен быть по пути к рулевому колесу существенно ослаблен.
Таким образом,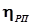 
=(0,5…0,65) 
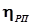, что составляет =(0,85…0,9).
Пренебрегая трением в подшипниках, сальниках и т. п. КПД червячного и винтового механизмов могут быть определены по выражениям:
— в прямом направлении – 
,
— в обратном направлении – 
,
где: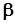 
– угол подъема винтовой линии червяка или винта в среднем сечении; 
– угол трения.