Цель работы: Использование процедуры «Поиск решения» для нахождения целочисленного решения задач линейного программирования.
Содержание работы:
- найти целочисленное решение заданной задачи линейного программирования.
- определить дефицитное сырье (сырье, которое в процессе работы используется полностью).
- найти зависимость целочисленного решения задачи от количества дефицитного сырья.
- найти зависимость целочисленного решения задачи от технологий (меняя величины затрат дефицитного материала на производство единицы продукции каждого вида).
Записываем исходные данные (лаб. раб. №1):
| А | B | C | D | E | F | G | |
| Сырье | Нормы затрат на ед. продукции | Количество сырья | Левая часть ограничений | Остаток сырья | |||
| A | B | C | |||||
| 1в | |||||||
| 2в | |||||||
| 3в | |||||||
| 4в | |||||||
| Цена ед. продукции | |||||||
| x1 | x2 | x3 | Целевая ф-ия | ||||
После введения формул для левых частей ограничений, остатков сырья и целевой функции (лаб. раб. №1) будем иметь:
| А | B | C | D | E | F | G | |||
| Сырье | Нормы затрат на ед. продукции | Количество сырья | Левая часть ограничений | Остаток сырья | |||||
| A | B | C | |||||||
| 1в | |||||||||
| 2в | |||||||||
| 3в | |||||||||
| 4в | |||||||||
| Цена ед. продукции | |||||||||
| x1 | x2 | x3 | Целевая ф-ия | ||||||
|
|
Вызываем процедуру «Поиск решения».Указываем,что целевая функция находится в ячейке F11 и что ее нужно максимизировать.Также указываем на неотрицательность и целочисленность переменных. Записываем ограничения
F3 ≤ E3, F4 ≤ E4, F5 ≤ E5, F6 ≤ E6
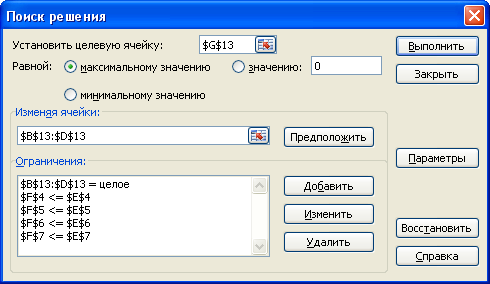
После выполнения вичислений получим:
| А | B | C | D | E | F | G | |
| Сырье | Нормы затрат на ед. продукции | Количество сырья | Левая часть ограничений | Остаток сырья | |||
| A | B | C | |||||
| 1в | |||||||
| 2в | |||||||
| 3в | |||||||
| 4в | |||||||
| Цена ед. продукции | |||||||
| x1 | x2 | x3 | Целевая ф-ия | ||||
Наиболее дефицитным является сырье 4-го вида. Находим решение целочисленной задачи для значений М4 ={35; 56; 77; 98; 119; 140; 161}.
Поле выполнения вычислений получим:
| А | B | C | D | E | F | G | |
| Сырье | Нормы затрат на ед. продукции | Количество сырья | Левая часть ограничений | Остаток сырья | |||
| A | B | C | |||||
| 1в | |||||||
| 2в | |||||||
| 3в | |||||||
| 4в | |||||||
| Цена ед. продукции | |||||||
| x1 | x2 | x3 | Целевая ф-ия | ||||
|
|
| А | B | C | D | E | F | G | |
| Сырье | Нормы затрат на ед. продукции | Количество сырья | Левая часть ограничений | Остаток сырья | |||
| A | B | C | |||||
| 1в | |||||||
| 2в | |||||||
| 3в | |||||||
| 4в | |||||||
| Цена ед. продукции | |||||||
| x1 | x2 | x3 | Целевая ф-ия | ||||
| А | B | C | D | E | F | G | |
| Сырье | Нормы затрат на ед. продукции | Количество сырья | Левая часть ограничений | Остаток сырья | |||
| A | B | C | |||||
| 1в | |||||||
| 2в | |||||||
| 3в | |||||||
| 4в | |||||||
| Цена ед. продукции | |||||||
| x1 | x2 | x3 | Целевая ф-ия | ||||
| А | B | C | D | E | F | G | |
| Сырье | Нормы затрат на ед. продукции | Количество сырья | Левая часть ограничений | Остаток сырья | |||
| A | B | C | |||||
| 1в | |||||||
| 2в | |||||||
| 3в | |||||||
| 4в | |||||||
| Цена ед. продукции | |||||||
| x1 | x2 | x3 | Целевая ф-ия | ||||
|
|
| А | B | C | D | E | F | G | |
| Сырье | Нормы затрат на ед. продукции | Количество сырья | Левая часть ограничений | Остаток сырья | |||
| A | B | C | |||||
| 1в | |||||||
| 2в | |||||||
| 3в | |||||||
| 4в | |||||||
| Цена ед. продукции | |||||||
| x1 | x2 | x3 | Целевая ф-ия | ||||
| А | B | C | D | E | F | G | |
| Сырье | Нормы затрат на ед. продукции | Количество сырья | Левая часть ограничений | Остаток сырья | |||
| A | B | C | |||||
| 1в | |||||||
| 2в | |||||||
| 3в | |||||||
| 4в | |||||||
| Цена ед. продукции | |||||||
| x1 | x2 | x3 | Целевая ф-ия | ||||
| А | B | C | D | E | F | G | |
| Сырье | Нормы затрат на ед. продукции | Количество сырья | Левая часть ограничений | Остаток сырья | |||
| A | B | C | |||||
| 1в | |||||||
| 2в | |||||||
| 3в | |||||||
| 4в | |||||||
| Цена ед. продукции | |||||||
| x1 | x2 | x3 | Целевая ф-ия | ||||
| Таким образом, имеем зависимость стоимости продукции от сырья 4-го вида (наиболее дефицитного): | ||||||||||||||||
|
Выясним степень влияния технологий на оптимальное решение. Для этого изменим величины затрат дефицитного материала:
| А | B | C | D | E | F | G | |
| Сырье | Нормы затрат на ед. продукции | Количество сырья | Левая часть ограничений | Остаток сырья | |||
| A | B | C | |||||
| 1в | |||||||
| 2в | |||||||
| 3в | |||||||
| 4в | |||||||
| Цена ед. продукции | |||||||
| x1 | x2 | x3 | Целевая ф-ия | ||||
Сравнивая полученное решение с решением исходной задачи, видим, что технологии сильно влияют на оптимальное решение
Лабораторная работа № 4.
ТРАНСПОРТНАЯ ЗАДАЧА
Цель работы: Использование процедуры «Поиск решения» для составления оптимального плана перевозок.
Содержание работы:
- ввод исходных данных.
- запись формул целевой функции и ограничений для стандартной транспортной задачи.
- нахождение решения стандартной транспортной задачи, используя процедуру «Поиск решения».
- решение транспортной задачи при наличии дополнительных ограничений (ограничение количества перевозимых изделий в определенном направлении, задание количества перевозимых изделий в заданном направлении и т. д.)
Постановка задачи: Задана матрица С стоимостей перевозки единицы товара, вектор производства а (количество товара, производимого каждым производителем), вектор потребления b (количество товара, потребляемого каждым потребителем).
С =  а= (30; 5; 45; 70) b= (10; 35; 16; 25; 35)
а= (30; 5; 45; 70) b= (10; 35; 16; 25; 35)
Составить план перевозок, чтобы суммарные транспортные расходы были минимальными.
Решение.
Суммарное количество производимого товара равно 150. Суммарное количество потребляемого товара равно 121. Введем фиктивного потребителя с объемом потребления 150-121=29. Стоимость перевозки к фиктивному потребителю возьмем больше любой другой стоимости, например, 10. Тогда исходные данные запишутся:
С 1=  а= (30; 5; 45; 70) b 1 = (10; 35; 16; 25; 35; 29)
а= (30; 5; 45; 70) b 1 = (10; 35; 16; 25; 35; 29)
В Excel вводим исходные данные, выделяем место для решений (B10:G13),полагая начальные значения 0 или любые другие числа. Записываем в ячейку I10 формулу для количества товара, вывезенного от 1-го производителя:
| A | B | C | D | E | F | G | H | I | |
| Матр. стоимостей | Произво- дители | ||||||||
| Потребители | |||||||||
| Матр. перевозок | Вывезено от производителей | ||||||||
| =cумм(B10:G10) | |||||||||
| Завезено потребителям |
После ввода этой формулы (ENTER) и протаскиванию по ячейкам I11:I13 получим
| A | B | C | D | E | F | G | H | I | |
| Матр. стоимостей | Произво- дители | ||||||||
| Потребители | |||||||||
| Матр. перевозок | Вывезено от производителей | ||||||||
| Завезено потребителям |
В B15 записываем формулу для количества товара,завезенного 1-му потребителю:
| A | B | C | D | E | F | G | H | I | |||
| Матр. стоимостей | Произво- дители | ||||||||||
| Потребители | |||||||||||
| Матр. перевозок | Вывезено от производителей | ||||||||||
| Завезено потребителям | =сумм (B10:B13) | ||||||||||
После введения формулы и протаскивания на ячейки C15:G15 получим:
| A | B | C | D | E | F | G | H | I | |
| Матр. стоимостей | Произво- дители | ||||||||
| Потребители | |||||||||
| Матр. перевозок | Вывезено от производителей | ||||||||
| Завезено потребителям |
В I15 записываем формулу для целевой функции
| A | B | C | D | E | F | G | H | I | |
| Матр. стоимостей | Произво- дители | ||||||||
| Потребители | |||||||||
| Матр. перевозок | Вывезено от производителей | ||||||||
| Завезено потребителям | Цел. ф-ия | =суммпроизв(B2:F5;B10:F13) |
Введя формулу, получим
| A | B | C | D | E | F | G | H | I | |
| Матр. стоимостей | Произво- дители | ||||||||
| Потребители | |||||||||
| Матр. перевозок | Вывезено от производителей | ||||||||
| Завезено потребителям | Цел. ф-ия |
Вызываем процедуру «Поиск решения», указываем, что целевая функция должна достичь минимума, что целевая функция находится в ячейке I17 и что изменять нужно ячейки B10:G10. Далее нужно добавить ограничения неотрицательности и целочисленности решений. Также добавим ограничения, указывающие, что весь товар дожжен быть вывезенным от производителей и завезен потребителям (включая фиктивные):
I10=H2
I11=H3
I12=H4
I13=H5
B15=B7
C15=C7
D15=D7
E15=E7
F15=F7
G15=G7
После вычислений получим
| A | B | C | D | E | F | G | H | I | |
| Матр. стоимостей | Произво- дители | ||||||||
| Потребители | |||||||||
| Матр. перевозок | Вывезено от производителей | ||||||||
| Завезено потребителям | Цел. ф-ия |
Так как 6-ой потребитель является фиктивным, то соответствующее количество товара будет не вывезено от производителей. Таким образом, имеем следующий план перевозок:
| Потребит. Производит. | Остаток | |||||
Транспортные расходы составят 226 д.е.
Предположим теперь, что от 3-го производителя обязательно нужно вывезти не менее 30 единиц товара. Тогда нужно записать формулу для подсчета количества товара,вывезенного от 3-го производителя (без учета фиктивного потребителя)
| A | B | C | D | E | F | G | H | I | |
| Матр. стоимостей | Производители | ||||||||
| Потребители | |||||||||
| Матр. перевозок | Вывезено от производителей | ||||||||
| =сумм(B12: F12) | |||||||||
| Завезено потребителям | Цел. ф-ия |
После введения формулы получим
| A | B | C | D | E | F | G | H | I | |
| Матр. стоимостей | Производители | ||||||||
| Потребители | |||||||||
| Матр. перевозок | Вывезено от производителей | ||||||||
| Завезено потребителям | Цел. ф-ия |
Вызываем процедуру «Поиск решений».К предыдущим ограничениям нужно добавить
H12 ≥ 30. После выполнения решения получим
| A | B | C | D | E | F | G | H | I | |
| Матр. стоимостей | Произво- дители | ||||||||
| Потреби- тели | |||||||||
| Матр. перевозок | Вывезено от производителей | ||||||||
| Завезено потреби- телям | Цел. ф-ия |
Предположим теперь, что от 3-го производителя к 4-му потребителю можно завести только 10 единиц товара. Тогда к предыдущим условиям нужно добавить условие
E12 = 10
После выполнения решения получим: