Цель работы: Использование процедуры «Поиск решения» для решения задачи об оптимальном назначении n работников на n работ.
Содержание работы:
- ввод исходных данных (матрицы оценок выполнения работ каждым работником)
- запись формул целевой функции и ограничений.
- нахождение оптимального назначения работников на работы, используя процедуру «Поиск решения».
Постановка задачи: Задана матрица эффективностей С - матрица оценок выполнения заданных работ каждым работником (например, в пятибалльной системе):
Работы 1 2 3 4 5 6
С = 
Нужно распределить работников по работам так,чтобы все работы были выполнены при наибольшей эффективности. Решаем задачу в Excel.
Вводим матрицу эффективностей и матрицу назначений, первоначальные значения элементов которой полагаем равными нулю. Решение будем строить таким образом, чтобы элемент матрицы назначений аij =1, если i -тый работник назначен на j -ую работу. В противном случае аij =0.Так как число работников равно числу работ, то каждый работник может быть назначен только на одну работу и на каждую работу может бать назначен только один работник. Отсюда следует, что в каждой строке и в каждом столбце должно бать по одной одинице. Значит, сумма элементов любой строки и любого столбца дожна раняться единице. Единицы в матрице назначений должны располагаться таким образом, чтобы сумма элементов матрицы эффективностей, расположенных на местах единиц матрицы назначений, была максимальной. Это равносильно тому, что сумма призведений элементов матрицы эффективностей на соответствующие элементы матрицы назначений была максимальной.
|
|
В ячейку I 11 записываем формулу суммы 1-ой строки
| A | B | C | D | E | F | G | H | I | |
| работы работники | |||||||||
| Матрица эффективностей | |||||||||
| I | |||||||||
| II | |||||||||
| III | |||||||||
| IV | |||||||||
| V | |||||||||
| VI | |||||||||
| Матрица назначений | Сумма по строкам | ||||||||
| =сумм(B13:G13) | |||||||||
| Сумма по столбцам | |||||||||
| После введения формулы протягиваем ее на ячейки I 12: I 16. В ячейку B 18 записываем формулу суммы 1-го столбца строки |
| A | B | C | D | E | F | G | H | I | |
| работы работники | |||||||||
| Матрица эффективностей | |||||||||
| I | |||||||||
| II | |||||||||
| III | |||||||||
| IV | |||||||||
| V | |||||||||
| VI | |||||||||
| Матрица назначений | Сумма по строкам | ||||||||
| Сумма по столбцам | =сумм (B13:B18) | ||||||||
| Вводим формулу и протягиваем ее на другие столбцы. В ячейку I 18записываем формулу целевой функции. |
|
|
| A | B | C | D | E | F | G | H | I | |
| работы работники | |||||||||
| Матрица эффективностей | |||||||||
| I | |||||||||
| II | |||||||||
| III | |||||||||
| IV | |||||||||
| V | |||||||||
| VI | |||||||||
| Матрица назначений | Сумма по строкам | ||||||||
| Целевая ф-ия | |||||||||
| Сумма по столбцам | =суммпроизв(B4:G9; B13:G18) | ||||||||
|
|
После введения формулы получим
| A | B | C | D | E | F | G | H | I | |
| работы работники | |||||||||
| Матрица эффективностей | |||||||||
| I | |||||||||
| II | |||||||||
| III | |||||||||
| IV | |||||||||
| V | |||||||||
| VI | |||||||||
| Матрица назначений | Сумма по строкам | ||||||||
| Целевая ф-ия | |||||||||
| Сумма по столбцам | о |
Вызываем процедуру «Поиск решения», указываем, что целевая функция находится в ячейке I18 и что изменять нужно ячейки B11:G16. Далее нужно добавить ограничения неотрицательности и целочисленности решений. Также добавим ограничения, указывающие,что суммы по строкам и столбцам должны равняться единице:
I 11 =1
I 12 =1
I 13 =1
I 14 =1
I 15 =1
I 16 =1
B 18 =1
C 18 =1
D 18 =1
E 18 =1
F 18 =1
G 18 =1
После решения получим:
| A | B | C | D | E | F | G | H | I | |
| работы работники | |||||||||
| Матрица эффективностей | |||||||||
| I | |||||||||
| II | |||||||||
| III | |||||||||
| IV | |||||||||
| V | |||||||||
| VI | |||||||||
| Матрица назначений | Сумма по строкам | ||||||||
| Целевая ф-ия | |||||||||
| Сумма по столбцам |
Таким образом, имеем следующее распределение:
I-ый рабочий назначается на 2-ую работу, II-ой - на 3-юю, III-ий - на 4-ую, IV-ый - на 1-ую, V-ый - на 6-ую, VI-ой - на 5-ую.
Эффективность равна 27 баллов (максимально возможная 30 баллов).
Лабораторная работа № 6.
ОПТИМИЗАЦИЯ РАБОТНИКОВ.
Цель работы: Использование процедуры «Поиск решения» для решения задачи динамического программирования о распределении работников по периодам в зависимости от объемов заказов.
Содержание работы:
- ввод исходных данных (оптимального количества работников в каждый период, необходимых для выполнения).
- запись формул подсчета потерь от найма-увольнения и несоответствия реального количества работников оптимальному.
- формирование и запись формул целевой функции и ограничений.
- нахождение оптимального распределения работников, используя процедуру «Поиск решения».
Постановка задачи:
Производителю работ нужно определить оптимальное число работников в каждый из n месяцев. Производственные задания для каждого месяца известны. Допустим, что в j -ый месяц идеальное число рабочих mj. Если бы производитель работ мог увольнять и принимать новых рабочих без дополнительных затрат, то он мог бы в j -ый месяц принять ровно mj рабочих
(j=1,2,…,n).
Предположим, что работа j-го месяца может быть выполнена и меньшим числом рабочих при сверхурочной работе. Пусть xj фактическое число рабочих в j-ый месяц. Затраты по изменению численности рабочих при переходе от (j-1)-го месяца к j-му определяется функцией fj(xj- xj-1).
В зависимости от знака величины xj- xj-1 функция fj(xj- xj-1) определяет затраты по найму или увольнению. Очевидно, fj(0)=0. Отклонение численности рабочих от mj приводит к расходам gj(xj-mj), причем gj(0)=0;
j=1,2,…n. Считаем, что в начальный момент число рабочих составило с .
Нужно определить число работников в каждом месяце так, чтобы суммарные потери от найма-увольнения и несоответствия реального количества работников оптимальному были минимальными.
Пример: Рассмотрим задачу об использовании рабочей силы на двeннадцать
периода: j=1,2, ….12
Пусть m0=2, m1=2, m2=5, m3=3, m4=1, m5=6, m6=2, m7=4, m8=8, m9=3,
m10=5, m11=7, m12=3.
Пусть fj(xj) и gj(xj) имеют вид:
fj(xj)= 
gj(xj)= 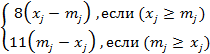
Решение:
В Excel введем исходные данные, полагая x0 = m0 =2. Искомые значения xj
первоначально полагаем равными mj. В ячейку F6 логическую формулу для вычисления
затрат, если х1 не равно х0:
| A | B | C | D | E | F | G | |
| a1 | a2 | b1 | b2 | ||||
| Затраты по приему, | |||||||
| m0= | x0= | увольнению | |||||
| m1= | x1= | Если(D6>D5);$A$2*(D6-D5);$B$2*(D5-D6)) | |||||
| m2= | x2= | ||||||
| m3= | x3= | ||||||
| m4= | x4 | ||||||
| m5= | x5= | ||||||
| m6= | x6= | ||||||
| m7= | x7= | ||||||
| m8= | x8= | ||||||
| m9= | x9= | ||||||
| m10= | x10= | ||||||
| m11= | x11= | ||||||
| m12= | x12= | ||||||
После введения формулы, протягивания ее на ячейки F7: F17 и записи в G6 формулы для вычисления затрат, если х1 не равно m1, получим:
| A | B | C | D | E | F | G | |
| a1 | a2 | b1 | b2 | ||||
| Затраты по, приему | Затраты по несоответствию | ||||||
| m0= | x0= | увольнению | оптимуму | ||||
| m1= | x1= | Если(D6>B6);$C$2*(D6-B6);$D$2*(B6-D6)) | |||||
| m2= | x2= | ||||||
| m3= | x3= | ||||||
| m4= | x4 | ||||||
| m5= | x5= | ||||||
| m6= | x6= | ||||||
| m7= | x7= | ||||||
| m8= | x8= | ||||||
| m9= | x9= | ||||||
| m10= | x10= | ||||||
| m11= | x11= | ||||||
| m12= | x12= |
После введения формулы, протягивания ее на ячейки G7: G17, записываем формулу целевой функции в ячейку G19
| A | B | C | D | E | F | G | |
| a1 | a2 | b1 | b2 | ||||
| Затраты по, приему | Затраты по несоответствию | ||||||
| m0= | x0= | увольнению | оптимуму | ||||
| m1= | x1= | ||||||
| m2= | x2= | ||||||
| m3= | x3= | ||||||
| m4= | x4 | ||||||
| m5= | x5= | ||||||
| m6= | x6= | ||||||
| m7= | x7= | ||||||
| m8= | x8= | ||||||
| m9= | x9= | ||||||
| m10= | x10= | ||||||
| m11= | x11= | ||||||
| m12= | x12= |
| Цел. ф-ия = | =СУММ(F6: G17) |
После введения формулы вызываем процедуру «Поиск решения», указываем, что целевая функция находится в ячейке G19 и что изменять нужно ячейки D6:D17. Далее нужно добавить ограничения неотрицательности и целочисленности решений.
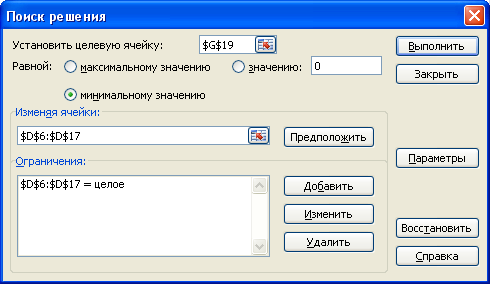
После решения получим:
| A | B | C | D | E | F | G | |
| a1 | a2 | b1 | b2 | ||||
| Затраты по, приему | Затраты по несоответствию | ||||||
| m0= | x0= | увольнению | оптимуму | ||||
| m1= | x1= | 2,473E-07 | 3,887E-07 | ||||
| m2= | x2= | ||||||
| m3= | x3= | ||||||
| m4= | x4 | ||||||
| m5= | x5= | ||||||
| m6= | x6= | ||||||
| m7= | x7= | ||||||
| m8= | x8= | ||||||
| m9= | x9= | ||||||
| m10= | x10= | ||||||
| m11= | x11= | ||||||
| m12= | x12= |
| Цел. ф-ия = |
Таким образом, наименьшие затраты оставят 191 д.е. при распределении работников по периодам, указанном в ячейках D6:D17.
Лабораторная работа № 7.