Экспериментальное построение диаграмм

ДИАГРАММА СОСТОЯНИЯ

Правило фаз

Диаграмма состояния представляет собой графическое изображение состояния сплава. Если изменяется состав сплава, его температура, давление и состояние сплава также изменяется, то это находит гра­фическое отображение в диаграмме состояния.

Диаграмма состояния показывает устойчивые состояния, т. е. состояния, которые при данных условиях обладают минимумом сво­бодной энергии. Поэтому диаграмма состояния может также назы­ваться диаграммой равновесия, так как она показывает, какие при данных условиях существуют равновесные фазы. В соответствии с этим и изменения в состоянии, которые отражены на диаграмме, относятся к равновесным условиям, т. е. при отсутствии перенагрева или переохлаждения. Однако, как мы видели раньше, равновесные превращения, т. е. превращения в отсутствие переохлаждения или перенагрева, в действительности не могут совершаться, поэтому диаграмма состояния представляет собой теоретический слу­чай, а в практике используется для рассмотрения превращений при малых скоростях нагрева или охлаждения.

Общие закономерности сосуществования устойчивых фаз, отве­чающих теоретическим условиям равновесия, могут быть выражены в математической форме, именуемой правилом фаз, или законом Гиббса.

Правило фаз дает количественную зависимость между степенью свободы системы и количеством фаз и компонентов.

Фазой называется однородная часть си­стемы, отделенная от других частей системы (фаз) поверхностью раздела при пере­ходе через которую химический состав или структура вещества изменяется скачком.

Следовательно, однородная жидкость является однофазной систе­мой, а механическая смесь двух видов кристаллов — двухфазной, так как каждый кристалл отличается от другого по составу или по строению и они отделены один от другого поверхностью раздела.

Компонентами называются вещества, об­разующие систему. Следовательно, чистый металл пред­ставляет собой однокомпонентную систему, сплав двух металлов — двухкомпонентную и т.д. Химические соединения можно рассма­тривать как компоненты лишь в том случае, если они не диссоциируют на составные части в исследуемых интервалах температур.

Под числом степеней свободы (вариант­ностью) системы понимают число внешних и внутренних факторов (температура, давле­ние и концентрация), которое можно из­менять без изменения числа фаз в системе.

Если число степеней свободы равно нулю (нонвариантная система) то, очевидно, нельзя изменять внешние и внутренние факторы си­стемы (температуру, давление, концентрацию) без того, чтобы это не вызвало изменения числа фаз.

Если число степеней свободы равно единице (моновариантная система), то возможно изменение в некоторых пределах одного из перечисленных факторов и это не вызовет уменьшения или увеличения числа фаз.

Правило фаз представляет собой математическое выражение ус­ловия равновесия системы, т. е. уравнение правила фаз показывает количественную зависимость между числом степеней свободы системы с и числом компонентов k и фаз f:

C = k – f + 2

При выводе уравнения правила фаз исходили из того, что термодинамический потенциал каждого компонента во всех сосуществующих фазах минимален, поэтому система не стремится ни к каким изме­нениям и находится в равновесном состоянии. Правило фаз и все связанные с ним выводы справедливы только для равновесного со­стояния.

Независимыми переменными в уравнении правила фаз являются концентрация, температура и давление. Если принять, что все пре­вращения в металле происходят при постоянном давлении, то число переменных уменьшится на единицу (давление постоянно), и урав­нение правила фаз примет следующий вид:

с = k — f + 1.

Это выражение правила фаз будем применять к металлическим системам равновесия, считая давление во всех процессах неизменным.

Посмотрим, как изменяется степень свободы однокомпонентной системы (k = 1) для случая кристаллизации чистого металла. Когда металл находится в жидком состоянии, т. е. f = 1 (одна фаза — жидкость), число степеней свободы равно 1 (с = k — f + 1=1 – 1 + 1 = 1).

Температуру в данном случае можно изменять, не изменяя агре­гатного состояния. В момент кристаллизации f = 2 (две фазы — твердая и жидкая),

с = k — f + 1=1 – 2 + 1 = 0. Это значит, что две фазы находятся в равновесии при строго определенной темпе­ратуре (температуре плавления), и она не может быть изменена до тех пор, пока одна из фаз не пропадет, т. е. система не станет моно­вариантной (с = 1).

Экспериментальное построение диаграмм

Обычно для построения диаграмм состояния пользуются результа­тами термического анализа, т.е. строят кривые охлаждения и по остановкам и перегибам на этих кривых, вызванным тепловым эффек­том превращений, определяют температуры превращения.

Температуру металлов измеряют обычно при помощи термопары.

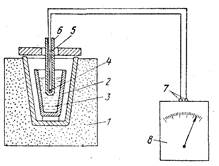
Температура кристаллизации определяется следующим образом. В печь 1 (рис. 1) помещают тигелек 2, в котором расплавляют исследуемый сплав 3. Затем в расплав погружают горячий спай 4 термопары 5 (защищенной фарфоровым или кварцевым колпачком 6) и выклю­чают печь. Начинается охлаждение и температуру отмечают через определен­ные промежутки времени. Появление изменений в агрегатном состоянии в связи с выделением скрытой теплоты превра­щения отражается на кривой темпера­тура — время.

Имея достаточное количество спла­вов и определив в каждом сплаве температуры превращений, можно построить диаграмму состояния.

Для более точного построения диа­граммы состояния в дополнение к термическому методу изучают с помощью микроскопа и рентгеновских лучей структуру сплавов разного состава и по-разному обработанных термически, изме­ряют разнообразнейшие физические свой­ства сплавов и т.д.

Вид диаграммы определяется характером взаимодействий, кото­рые возникают между компонентами в жидком и твердом состояниях. Во всех случаях пред­полагают, что в жидком состоянии существует неограниченная растворимость, т. е. однородная фаза (в дальнейшем будет обозначаться буквой L) существует при любом соотношении ком­понентов.