Двойные числовые ряды
Кратные ряды.
Кратным рядом называется выражение
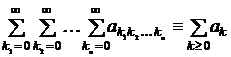 ,
,  C (1)
C (1)
где 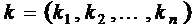 - так называемый мультииндекс.
- так называемый мультииндекс.
Если  - тоже мультииндекс, то неравенство
- тоже мультииндекс, то неравенство  означает, что
означает, что 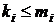
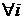 , а неравенство
, а неравенство  означает, что
означает, что 
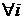 .
.
Выражения

называются частичными суммами ряда (1).
Если существует предел, называемый суммой ряда (1)
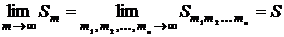 ,
,
то ряд (1) называется сходящимся, если 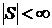 .
.
В теории сходимости кратных рядов есть моменты, отличающие эту теорию от теории сходимости обычных рядов. Все эти различия можно проиллюстрировать на двойных рядах. Для того, чтобы избежать громоздких выкладок, в дальнейшем ограничимся двойными рядами.
Сходимость двойных рядов.
Рассмотрим двойной ряд
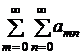 ,
, 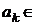 С (2)
С (2)
Элементы этого ряда можно расположить в виде бесконечной прямоугольной матрицы
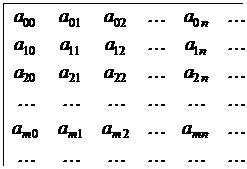 (
( )
)
Такого рода матрицы называют матрицами с двумя входами.
Частными суммами ряда (2) мы называем выражения
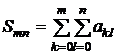
Если существует предел, называемый суммой ряда (2),
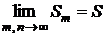 ,
,
То ряд (2) называется сходящимся, если 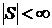 и расходящимся в противном случае.
и расходящимся в противном случае.
На двойные ряды легко переносятся два свойства обычных, однократных рядов:
1) Если ряд (2) сходится и имеет сумму  , а
, а  , то ряд
, то ряд
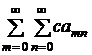
Также сходится и его сумма равна 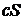 .
.
2) Сумма (или разность) двух сходящихся двойных рядов с суммами  и
и 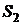 соответственно есть снова сходящийся ряд с суммой
соответственно есть снова сходящийся ряд с суммой 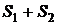 (или
(или 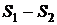 ).
).
Доказательства этих свойств предоставляю сделать самим слушателям.
Точно так же сохраняется необходимое условие сходимости двойного ряда: если ряд (2) сходится, то его общий член стремится к нулю при  и
и  , т.е.
, т.е.
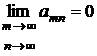 .
.
Это сразу видно из равенства
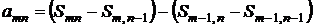 .
.
Однако из сходимости двойного ряда (2) не следует, что
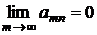 ,
, 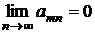
Например, рассмотрим матрицу 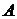


Для ряда, составленного из элементов этой матрицы имеем 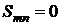 при
при  и
и  , т.е. ряд сходится и сумма его равна нулю. В то же время видно, что
, т.е. ряд сходится и сумма его равна нулю. В то же время видно, что
 ,
, 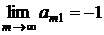
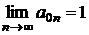 ,
,  .
.
Можно построить так же примеры таких матриц, что при некоторых фиксированных 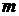
 ,
,
xотя ряд (2) сходится (см. матрицу  ).
).
Такая патология структуры сходящихся двойных рядов приводит к тому, что наряду с их обычной сходимостью целесообразно рассматривать сходимость с различными ограничениями. Чаще всего рассматривают следующие два вида сходимости: ограниченную и регулярную.
- Ряд (2) называется ограниченно сходящимся, если он сходится и все его частные суммы ограничены.
- Рассмотрим наряду с рядом (2) так называемые повторные ряды
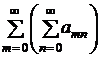 и
и 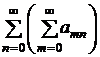 (3)
(3)
Если вместе с рядом (2) сходятся оба ряда (3), то ряд (2) называется регулярно сходящимся.
Лемма 1. Если ряд (2) сходится регулярно к сумме  , то оба повторных ряда (3) сходятся к той же сумме.
, то оба повторных ряда (3) сходятся к той же сумме.
Доказательство. Введём обозначения
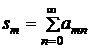 ,
, 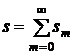 ,
, 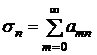 ,
, 
Имеем следующее равенство:
 ,
,
или
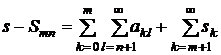 .
.
В силу регулярной сходимости ряда (2), существует натуральное число 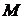 такое, что
такое, что
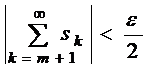 ,
,  ,
,
где 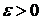 - любое наперёд заданное сколь угодно малое число. Зафиксировав
- любое наперёд заданное сколь угодно малое число. Зафиксировав 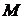 , выберем числа
, выберем числа 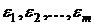 так, чтобы
так, чтобы
 (
(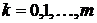 ;
; 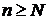 ;
;  )
)
Это можно сделать в силу регулярной сходимости ряда (2). Получим тогда, что
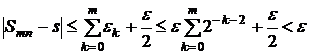 , если
, если  ,
, 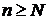 .
.
Аналогично из равенства

Будем иметь
 для
для 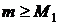 ,
, 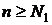
Следовательно, 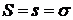 , ч. т. д.
, ч. т. д.
Замечание. Из сходимости ряда (2) не следует сходимость повторных рядов (3), что видно из предыдущего примера, т. е. не следует регулярная сходимость ряда (2).
Обратно: из сходимости повторных рядов и равенства 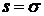 не следует сходимость ряда (2). Действительно, если взять матрицу
не следует сходимость ряда (2). Действительно, если взять матрицу
 ,
,
то 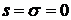 , в то время как
, в то время как  не существует, т. к.
не существует, т. к. 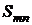 принимает бесконечно много раз значения 0 и 1.
принимает бесконечно много раз значения 0 и 1.
Однако можно утверждать следующее:
Теорема 1. Если сходится двойной ряд (2) и сходятся ряды по строкам, т. е.  сходятся ряды
сходятся ряды 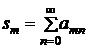 , то сходится повторный ряд
, то сходится повторный ряд 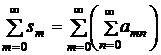 и имеет ту же сумму
и имеет ту же сумму  , что и двойной ряд.
, что и двойной ряд.
Доказательство теоремы 1 вытекает из основной теоремы о связи между повторными и двойными пределами для функции двух переменных.
Теорема 2. (о повторных пределах). Пусть функция 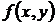 определена на множестве
определена на множестве  ,
, 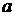 и
и  – точки сгущения множеств
– точки сгущения множеств 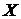 и
и  соответственно, им не принадлежащие. Если
соответственно, им не принадлежащие. Если
1) существует (конечный или нет) двойной предел

и 2) при любом 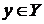 существует конечный простой предел по
существует конечный простой предел по 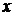
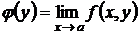 , то существует повторный предел
, то существует повторный предел
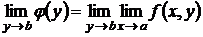
и равен двойному.
Доказательство проведём для случая конечных 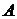 ,
, 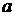 и
и  . По определению предела функции, по заданному
. По определению предела функции, по заданному 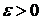 найдётся такое
найдётся такое  , что
, что
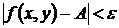 , (4)
, (4)
лишь только 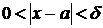 и
и 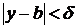 , причём
, причём 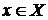 , а
, а 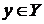 . Фиксируем теперь
. Фиксируем теперь  так, чтобы выполнялось неравенство
так, чтобы выполнялось неравенство 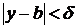 и перейдём в (4) к пределу, устремив
и перейдём в (4) к пределу, устремив 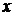 к
к 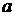 . Т. к. при этом, в виду условия 2) теоремы,
. Т. к. при этом, в виду условия 2) теоремы, 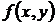 стремится к пределу
стремится к пределу 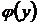 , то получим
, то получим 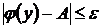 .
.
Вспомнив, что здесь  любое число из
любое число из  , подчинённое условию
, подчинённое условию 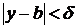 , приходим к заключению, что, по определению предела
, приходим к заключению, что, по определению предела
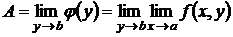 , ч. т. д.
, ч. т. д.
Замечание. Если наряду с условиями 1) и 2) при любом 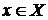 существует конечный простой предел
существует конечный простой предел
 ,
,
то, как следует из доказанного, если 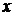 и
и  поменять ролями, существует и другой повторный предел
поменять ролями, существует и другой повторный предел
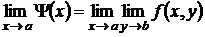
и равен числу 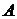 : в этом случае оба повторных предела равны.
: в этом случае оба повторных предела равны.
Теперь теорема 1 легко следует из этого результата. В теореме 1 роль независимых переменных играют 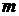 и
и  ,
, 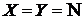 ,
, 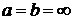 , а частная сумма
, а частная сумма 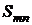 - роль функции
- роль функции 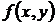 . Тогда по теореме о повторных пределах,
. Тогда по теореме о повторных пределах,
 .
.
Аналогичная теорема имеет место и для второго повторного ряда (3).
Теперь мы можем установить критерий регулярной сходимости ряда (2) – аналог критерия Коши для сходимости обычных рядов.
Теорема 3. (критерий регулярной сходимости).
Для того, чтобы ряд (2) сходился регулярно, необходимо и достаточно, чтобы для любого наперёд заданного 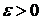 существовало натурально число
существовало натурально число  такое, что
такое, что
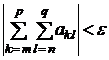 (5)
(5)
для всех 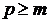 ,
,  и
и  или
или 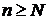 .
.
Доказательство. 1) Необходимость. Поскольку
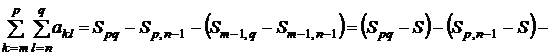
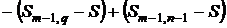 ,
,
то для заданного 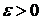 можно найти натуральное
можно найти натуральное  такое, что для всех
такое, что для всех  и
и 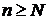 будут выполняться неравенства
будут выполняться неравенства
 ,
, 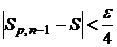 ,
, 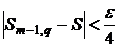 ,
, 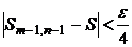
в силу сходимости ряда (2), и, следовательно, справедливо неравенство (5).
Докажем теперь необходимость в случае, когда только  или
или 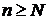 . Для этого обозначим через
. Для этого обозначим через  , где числа
, где числа 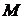 и
и  определены в лемме 1. Теперь неравенство (5) надо доказать лишь для случая, когда либо
определены в лемме 1. Теперь неравенство (5) надо доказать лишь для случая, когда либо  , либо
, либо 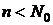 . Рассмотрим случай
. Рассмотрим случай  . Пусть
. Пусть 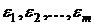 - те же числа, что и в доказательстве леммы 1. Обозначим через
- те же числа, что и в доказательстве леммы 1. Обозначим через  натуральное число такое, что
натуральное число такое, что
 ,
, 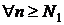 ,
,
откуда получаем
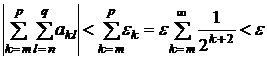 .
.
Аналогично в случае 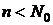 можно найти натуральное число
можно найти натуральное число 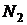 такое, что
такое, что
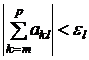 ,
, 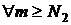 ,
,
откуда получаем
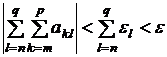 .
.
Полагая теперь 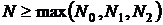 , получим, что имеет место неравенство (5).
, получим, что имеет место неравенство (5).
2) Достаточность. Пусть для сходящегося ряда (2) имеет место (5). Требуется доказать, что ряд (2) сходится регулярно, т.е. сходятся повторные ряды (3). Предположим, что (5) выполнено для всех  и
и 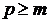 ,
,  . Перейдём в левой части неравенства (5) к пределу, когда
. Перейдём в левой части неравенства (5) к пределу, когда 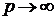 и
и 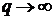 . Получим:
. Получим:
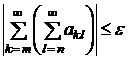 ,
, 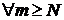 .
.
Следовательно, сходится ряд
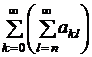 ,
,
и, значит, сходятся вес ряды по строкам
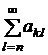
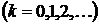
и, тогда сходятся и все ряды по строкам
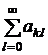
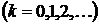 .
.
Отсюда, по теореме 1 вытекает, что сходится повторный ряд
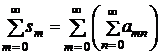
и имеет ту же сумму  , что и двойной ряд (2).
, что и двойной ряд (2).
Аналогично доказывается сходимость повторного ряда
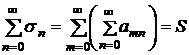 ,
,
которая вытекает из того, что (5) выполняется для всех 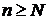 и
и 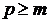 ,
,  .
.
Таким образом, ряд (2) сходится вместе с обоими повторными рядами и, значит, по определению, сходится регулярно.
Положительные ряды.
Остановимся на случае положительного ряда (2), т.е. ряда, все члены которого неотрицательны: 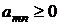
 .
.
Теорема 4. Для сходимости положительного ряда (2) необходимо и достаточно, чтобы его частичные суммы были ограниченны в совокупности.
Доказательство. 1) Необходимость этого утверждения почти очевидна: если ряд (2) сходится, то для любого 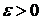 найдётся натуральный номер
найдётся натуральный номер  такой, что
такой, что 
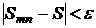 ,
,
так что для 
 .
.
Для конечного числа пар 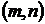 , у которых
, у которых  и
и 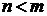 частные суммы
частные суммы 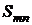 ограниченны некоторым числом
ограниченны некоторым числом 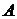 :
:  .
.
Наконец, если  , а
, а 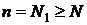 или
или 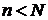 , а
, а  , то
, то 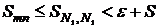 или
или 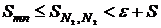 . В итоге, полагая
. В итоге, полагая 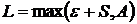 , будем иметь для всех
, будем иметь для всех 
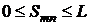 .
.
2) Достаточность. Пусть 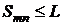
 . Рассмотрим
. Рассмотрим  и покажем, что
и покажем, что 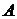 будет суммой нашего ряда. Зададим любое
будет суммой нашего ряда. Зададим любое 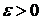 . По определению точной верхней грани, можно найти частную сумму
. По определению точной верхней грани, можно найти частную сумму  такую, что
такую, что
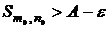 .
.
Если взять  , то и подавно
, то и подавно 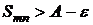 , т.к.
, т.к. 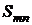 возрастает по каждой переменной
возрастает по каждой переменной 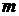 и
и  . Поскольку частная сумма
. Поскольку частная сумма 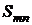 не превосходит
не превосходит 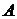 , то
, то 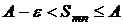 для
для  и, следовательно,
и, следовательно,
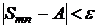
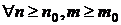 .
.
А это и означает, что
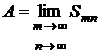 ,
,
т.е. ряд (2) сходится и его сумма равна 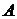 .
.
На основе теоремы 4 можно доказать теорему сравнения, аналогичную теореме сравнения для обычных положительных рядов.
Теорема 5. Пусть даны два положительных ряда
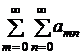 (А)
(А)
 (В)
(В)
Если для всех пар 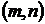 , у которых либо
, у которых либо  , либо
, либо 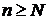 (
( - некоторое натуральное число) выполняется неравенство
- некоторое натуральное число) выполняется неравенство 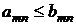 , то из сходимости ряда (В) вытекает сходимость ряда (А), а из расходимости ряда (А) следует расходимость ряда (В).
, то из сходимости ряда (В) вытекает сходимость ряда (А), а из расходимости ряда (А) следует расходимость ряда (В).
Доказательство. Поскольку отбрасывание конечного числа начальных членов ряда с номерами  и
и 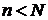 не отражается на его поведении, мы можем считать, не нарушая общности, что
не отражается на его поведении, мы можем считать, не нарушая общности, что 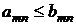
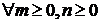 . Обозначая частные суммы рядов (А) и (В), соответственно, через
. Обозначая частные суммы рядов (А) и (В), соответственно, через 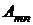 и
и 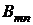 , будем иметь
, будем иметь
 .
.
Пусть ряд (В) сходится. Тогда, по теореме 4,
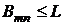
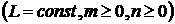 .
.
Тогда и подавно 
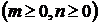 и, по той же теореме 4, ряд (А) сходится.
и, по той же теореме 4, ряд (А) сходится.
Обратно: если ряд (А) расходится, то расходится и ряд (В), т.к. в противном случае сходился бы ряд (А), что противоречит условию.
Теорема 6. Если из трёх рядов
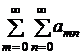 ,
,  ,
, 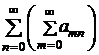
один сходится, то сходятся остальные и имеют ту же сумму.
Теорема 6 усиливает теорему 1.
Доказательство. Пусть сходится двойной ряд
 .
.
Тогда, очевидно, для его частных сумм будет справедливо неравенство:
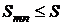
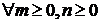 . (6)
. (6)
Далее, для любого 
 . (6')
. (6')
Это показывает, что ряд  сходится при любом
сходится при любом  . Если
. Если  - его сумма, то
- его сумма, то 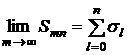 .
.
Переходя в неравенстве (6) к пределу при  , получим
, получим
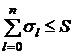 .
.
Видим, что эти суммы ограничены. Следовательно, ряд, составленный из  сходится и
сходится и 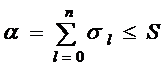 .
.
Мы доказали, что если сходится двойной ряд, то сходится и повторный, причём его сумма 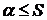 .
.
Теперь предположим, что сходится ряд 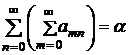 . Докажем, что тогда сходится и двойной ряд. Очевидно,
. Докажем, что тогда сходится и двойной ряд. Очевидно,
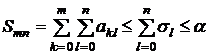 ,
,
так что частные суммы 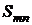 ограничены. Поэтому на основании теоремы 4 утверждаем, что двойной ряд сходится и имеет сумму
ограничены. Поэтому на основании теоремы 4 утверждаем, что двойной ряд сходится и имеет сумму  . Таким образом, сходимость одного из рядов влечёт сходимость другого и равенство их сумм:
. Таким образом, сходимость одного из рядов влечёт сходимость другого и равенство их сумм: 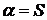 .
.
Теорема 7 (о связи двойного ряда и простого ряда, составленного из тех же членов).
Пусть двойной ряд с положительными членами
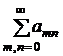
и простой ряд
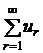 (7)
(7)
состоят из одних и тех же членов. Тогда из сходимости одного ряда вытекает сходимость другого и равенство их сумм.
Доказательство. Предположим сначала, что двойной ряд сходится и имеет конечную сумму  :
:
 .
.
Возьмём произвольное натуральное число 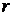 и составим частную сумму ряда (7):
и составим частную сумму ряда (7):
 .
.
Выберем теперь  и
и 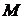 так, чтобы сумма
так, чтобы сумма  уже содержала в себе все элементы
уже содержала в себе все элементы 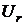 .
.
Тогда
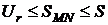 .
.
Значит, все частные суммы 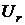 ограничены. Поэтому ряд (7) сходится и имеет сумму
ограничены. Поэтому ряд (7) сходится и имеет сумму
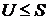 (8)
(8)
Предположим теперь, что сходится ряд (7). Возьмём произвольную частную сумму 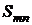 двойного ряда и найдём такое натуральное
двойного ряда и найдём такое натуральное 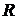 , чтобы все элементы частной суммы
, чтобы все элементы частной суммы 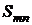 содержались среди первых
содержались среди первых 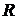 элементов ряда (7). Тогда справедливо неравенство
элементов ряда (7). Тогда справедливо неравенство
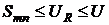 .
.
Отсюда следует, что двойной ряд сходится и имеет сумму
 (9)
(9)
Сопоставляя (8) и (9), имеем  .
.