Рассмотрим теперь двойной ряд, составленный из матрицы, в которой не все элементы положительны. Очевидно, что, как для простых рядов, мы можем исключить из рассмотрения те случаи, когда все элементы матрицы отрицательны или когда есть только конечное число положительных или отрицательных элементов, т.к. все эти случаи непосредственно приводятся к только что рассмотренному случаю положительных рядов. Поэтому мы предположим, что в рассматриваемой матрице (2'), а, значит и в ряде (2), есть бесконечное множество как положительных, так и отрицательных элементов.
Кроме матрицы (2'), составим ещё матрицу из абсолютных величин элементов
и из этой матрицы составим двойной ряд
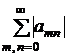(10)
Подобно соответствующей теореме о простых рядах, для двойных рядов имеет место теорема.
Теорема 8. Если сходится ряд (10), составленный из абсолютных величин ряда (2), то и ряд (2) сходится.
Доказательство. Представим 
в виде:
, (11)
где 
, 
.
Очевидно, что 
и 
. Т.к. 
и 
, то из сходимости двойного ряда (10), по теореме 5 (теореме сравнения) вытекает сходимость двойных рядов
, 
(12)
Но тогда сходится и ряд
и имеет сумму 
.
Определение. Если одновременно с рядом (2) сходится и ряд (10), то ряд (2) называется абсолютно сходящимся. Если же ряд (2) сходится, а ряд (10) расходится, то ряд (2) называется неабсолютно сходящимся (или условно сходящимся).
На абсолютно сходящиеся ряды распространяются основные свойства положительных рядов.
Теорема 9. Если ряд (2) сходится абсолютно, то ряды по строкам (и по столбцам)
так же сходятся абсолютно. Кроме того, сходится абсолютно и ряд, составленный из их сумм, и имеет ту же сумму, что и двойной ряд.
Доказательство. По теореме 6, из сходимости ряда (10) вытекает сходимость рядов по строкам
и их сумм
,
а так же сходимость ряда
.
Таким образом, доказана абсолютная сходимость рядов по строкам и повторного ряда по строкам. Равенство сумм двойного ряда и повторного ряда по строкам сразу следует из теоремы 1.
Теорема 10. Пусть даны двойной ряд (2) и простой ряд (7), состоящие из одних и тех же членов. Тогда абсолютная сходимость одного из них влечёт за собой абсолютную же сходимость другого и равенство их сумм.
Доказательство. По теореме 7, сходимость одного из рядов
, 
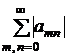влечёт за собой сходимость другого. Раз ряд (7) сходится абсолютно, то можно его члены расположить в любом порядке, удобном для вычисления его суммы, например, по квадратам, так, чтобы получилась исходная матрица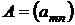 
:
,
где 
- переставленные члены ряда (7).
Тогда
, ч.т.д.
Следствие. Абсолютно сходящийся двойной ряд обладает переместительным свойством.
Доказательство В силу предыдущей теоремы, это прямо вытекает из аналогичного свойства простого ряда.
В заключение докажем две теоремы о повторных рядах.
Теорема 11. Пусть дан повторный ряд
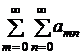. (13)
Если при замене его членов абсолютными величинами получается сходящийся ряд, то сходится не только повторный ряд (13), но и ряд
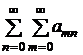, (14)
к той же сумме, что и ряд (13).
Доказательство: Утверждение теоремы 11 следует из теоремы 9, если учесть, что, по теореме 6, сходимость повторного ряда
равносильна сходимости двойного ряда
Теорема 12. Если простой ряд (7) сходится абсолютно, то, произвольно расположив его в виде матрицы 
c двумя входами, можно заменить ряд (7) повторным рядом (13) или (14).
Доказательство: немедленно следует из теорем 9 и 10: по теореме 10, из абсолютной сходимости ряда (7) следует абсолютная сходимость повторного ряда (2) и равенство их сумм, а, по теореме 9, сходятся оба повторных ряда (13) и (14) и имеет ту же сумму.
Примеры.
1) Ряд 
получается умножением рядов 
и 
, которые (абсолютно) сходятся при 
и 
; для этих же значений (абсолютно) сходится и двойной ряд.
Если 
или 
, то нарушается необходимое условие сходимости: общий член 
не стремится к нулю, когда 
и 
независимо стремятся к 
и ряд расходится. Легко проверить непосредственно, что расходимость налицо, когда 
или 
. Действительно, рассмотрим
Предполагается, что , а , будем иметь, что существует конечный предел 
, но не существует предела 
, т.к. 
есть частная сумма ряда 
, который расходится, поскольку не выполнено необходимое условие сходимости: 
, этот предел вообще не существует, если 
.
2) Рассмотрим ряд
.
Он также получается умножением рядов
и 
,
которые сходятся при 
и 
, так что двойной ряд при этих предположениях сходится. Наоборот, ес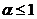ли 
(или 
), то двойной ряд расходится, ибо тогда расходятся все ряды по строкам (по столбцам) и тогда, по теореме 6, из расходимости повторного ряда следует расходимость двойного ряда.
3) Исследуем сходимость ряда
.
Так как члены, лежащие на одной диагонали, равны, то объединив их для удобства подсчета, получим ряд
.
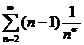Ввиду очевидных неравенств
,
деля на 
, будем иметь
.
Отсюда ясно, что полученный нами простой ряд сходится при 
и расходится при 
. По теореме 7, то же справедливо и для двойного ряда.
4) Рассмотрим теперь более сложный ряд
,
где форма 
предполагается положительной определенной. По критерию Сильвестра, необходимо и достаточно, чтобы все главные миноры определителя
были положительны, т.е. 
. Но тогда 
(если 
) и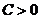 
. Если через 
обозначить наибольшее из чисел 
, то, очевидно,
.
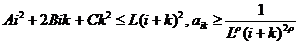В таком случае, из предыдущего примера 3) ясно, что при 
наш ряд расходится, в силу признака сравнения.
С другой стороны, имеем
.
Отсюда легко получить, что
.
аналогично получаем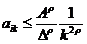 
. В итоге, 
, так что при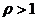 
наш ряд сходится, на основании примера 2).
5) Задача Х.Гольбаха. Пусть 
пробегает всевозможные степени с натуральными основаниями и показателями (большими единицы), и притом - каждую однажды.
Доказать, что
Если принимает всевозможные натуральные значения (>1), не являющиеся степенями, то
Отсюда 
,
где на этот раз пробегает уже все натуральные значения, начиная с 2, так что, действительно, 
.
Любопытно сопоставить этот результат с результатом Штейнера
(Здесь степени могут появляться и не однажды!)
6) Рассмотрим функцию двух переменных
.
Перемножая абсолютно сходящиеся ряды
, 
,
получим для этой функции (тоже абсолютно сходящийся по теореме Коши) двойной ряд
.
Поскольку абсолютно сходящийся двойной ряд обладает переместительным свойством, то на основании теорем 10 и 11 его можно преобразовать в повторный ряд, собирая члены с одинаковыми степенями 
:
Ряд 
, по определению, есть сумма двух рядов 
. Здесь для 
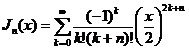, а для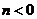 
Легко видеть, что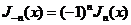 
.
Функция 
называется функцией Бесселя порядка . Эти функции играют важную роль в математической физике, небесной механике и т.д. функция 
, из разложения которой они получаются, носит название «производящей функции» для бесселевых функций.
7) Интересный пример дает матрица 
:
Здесь ряды по строкам абсолютно сходятся и имеют, соответственно, суммы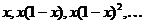 
Ряд, составленный из этих сумм, тоже абсолютно сходится, т.к. ряд
. Между тем другой повторный ряд не сходится, т.к. ряды по столбцам имеют суммы, равные 
или -1: для любого 
имеем
.
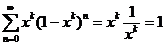Этот факт нисколько не противоречит теореме 11, т.к. для матрицы из абсолютных величин ни один повторный ряд не сходится. Иначе: абсолютная сходимость по строкам (столбцам) и абсолютная сходимость ряда из их сумм не может заменить требование сходимости повторного ряда из абсолютных величин.
8) Ряд Ламберта- это ряд
(15)
Покажем сначала следующее: если ряд
(А)
сходится, то ряд Ламберта (15) сходится при всех значениях 
; в противном случае он сходится как раз для тех значениях , для которых сходится степенной ряд
(16)
Доказательство: (K.Knopp) а) Пусть сначала ряд (А) расходится, так что радиус сходимости ряда (16) будет 
. Покажем, что для поведение рядов (15) и (16) одинаково.
Если сходится ряд (15), то сходится и ряд, полученный умножением его членов на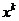 
, а следовательно, и ряд (16), как разность двух сходящихся рядов:
.
пусть теперь сходится ряд (16); тогда, по признаку Абеля сходится ряд, полученный умножением его членов на монотонно убывающие множители 
; т.е. сходится ряд 
, равно как и ряд 
. Следовательно, сходится и ряд (15), который представляет из себя сумму этих рядов:
.
Для ряд (16) заведомо расходится; мы утверждаем, что при этом значении расходится и ряд (15). Действительно, в противном случае из сходимости ряда
вытекала бы сходимость рядов
и 
,
вопреки предположению.
б) Если ряд (А) сходится (так что 
), то для ряд (16) сходится и сходимость ряда (15) устанавливается, как и выше. Остается показать, что ряд (15) сходится и при . Действительно, тогда 
и ряд
,
как упомянуто, сходится, следовательно, сходится ряд
.
Итак рассмотрим ряд Ламберта (15), ограничиваясь предположением, что . Мы видели, что при этом предположении ряд Ламберта сходится при тех же значениях , что и степенной ряд (16). Допустим, что радиус сходимости 
этого ряда 
и будем считать 
.
Очевидно, что
и ряд Ламберта (15) можно записать как двойной ряд
(17)
Сопоставим этому двойному ряду матрицу с двумя входами, помещая одинаковые степени в один столбец (пустые места можно заменить нулями):
Повторный ряд по строкам как раз и имеет сумму 
. Т.к. степенной ряд (16), а с ним и ряд Ламберта, сходится при замене на 
и 
на 
, то можно применить теорему 11 и просуммировать двойной ряд (17) по столбцам. Мы получим разложение в степенной ряд
, причем 
;
значок 
условно означает, что сумма распространяется лишь на делители 
числа .
Например, полагая 
или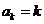 
(в обоих случаях, как легко проверить, 
, так что достаточно считать просто ), будем иметь соответственно:
, 
,
где 
означает число, а 
-сумму делителей .
9) Расположив члены двойного ряда (17) иначе, без пропусков:
 |
мы сохраняем те же суммы по строкам, по столбцам же получим, по порядку:
Таким образом, мы приходим к тождеству, связывающему функции и 
:
.
Например, взяв 
, где 
, будем иметь
,
так что
.
10) Обобщение ряда Ламберта.
Пусть даны два степенных ряда
и 
.
Предположим, что оба ряда абсолютно сходятся при . Составим матрицу с двумя входами из элементов 
и соответствующий двойной ряд
Так как (для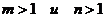 
) 
, то
и
Отсюда легко заключить, что двойной ряд, соответствующий взятой матрице, абсолютно сходится. Приравнивая, на основании теоремы 9, суммы повторных рядов, найдем тождество:
.
Отсюда тождество предыдущего примера получается при 
(так что 
).
Двойные степенные ряды.
Степенным рядом с двумя переменными и 
или двойным степенным рядом называется двойной ряд вида
, (18)
расположенный по целым, неотрицательным степеням переменных и .
Чтобы понять, какие задачи возникают в теории двойных степенных рядов, дадим обзор известных вам результатов из теории простых степенных рядов, т.е. степенных рядов одной переменной .
Степенным рядом называется ряд вида
. (19)
представляющий собой как бы «бесконечный многочлен», расположенный по возрастающим степеням переменной (
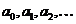-постоянные коэффициенты). поставим вопрос, какой вид имеет область сходимости степенного ряда, т.е. множество 
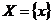. Верна следующая основная лемма:
Лемма. Если ряд (19) сходится для значения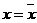 
, отличного от нуля, то он абсолютно сходится для любого значения , удовлетворяющего неравенству 
.
При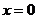 
сходится, очевидно, всякий ряд (19). Но есть степенные ряды, которые, помимо этого, не сходятся ни при одном значении . Примером такого «всюду расходящегося» ряда может служить ряд
, (20)
в чем можно убедиться, применяя признак Даламбера. Действительно, пусть таково, что 
. Тогда 
и, следовательно, общий член ряда (20) не стремится к нулю.
Рассмотрим теперь для ряда (19) множество 
, где 
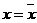и ряд (19) сходится при . Это множество может оказаться ограниченным сверху, либо нет. В последнем случае 
найдется такое 
, что и при указанном значении переменной , по основной лемме, ряд (19) абсолютно сходится. Таким образом, ряд (19) в этом случае сходится для любого 
и говорят, что радиус сходимости степенного ряда в этом случае 
, а область сходимости 
. Если же множество ограничено и - его точная верхняя граница, о ряд (19) абсолютно сходится для всех , удовлетворяющих неравенству , т.к., по определению точной верхней границы всегда найдется такое, что 
. В этом случае число называют радиусом сходимости, а интервал 
- областью сходимости ряда (19). О концах интервала сходимости, т.е. точках 
общего утверждения сделать нельзя: там, смотря по случаю, может быть как сходимость, так и расходимость.
Теорема Коши-Адамара. Радиус сходимости ряда (19)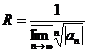 
. В частности, если существует 
, то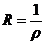 
Точно так же, если существует 
, то 
.
Рассмотрим два примера:
1) Ряд 
имеет радиус сходимости 
и интервал (область) сходимости 
.
Кроме того, при 
имеем ряд
,
т.е. знакопеременный ряд, который сходится по признаку Лейбница. Более того, легко найти его сумму. Известно, что для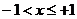 
,
и, следовательно,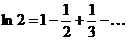 
При 
имеем
расходимость. В итоге, область сходимости нашего ряда есть полуинтервал 
.
2) Ряд
дает разложение по степеням функции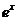 
. Его радиус сходимости 
, а интервал сходимости есть .
Свойства степенных рядов
Пусть степенной ряд (19) имеет радиус сходимости 
. Тогда
1) Для любого 
ряд (19) сходится равномерно на 
.
2) Сумма степенного ряда (19) для всех 
является непрерывной функцией.
3) Если два степенных ряда 
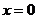в окрестности точки имеют одну и ту же сумму, то эти ряды тождественны, т.е. 
.
4) Если степенной ряд (19) расходится на конце 
промежутка сходимости, то на 
его сходимость не может быть равномерной.
5) Если степенной ряд сходится при , то сходимость ряда будет равномерной на 
.
6) Если степенной ряд (19) сходится при , то его сумма сохраняет непрерывность и при этом значении (
теорема Абеля), т.е.
.
7) Степенной ряд (19) в промежутке 
, где всегда можно интегрировать почленно, т.е.
.
Здесь возможно равенство , если в точках ряд (19) сходится.
8) Степенной ряд внутри его области сходимости можно почленно дифференцировать: их области сходимости совпадают
.
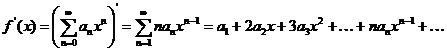9) Функция , представимая рядом (19) имеет в промежутке сходимости производные всех порядков. Сам ряд (19), по отношению к этой функции является ее рядом Тейлора, т.е.
Замечание. Отметим, что часто встречаются степенные ряды по возрастающим степеням разности 
, т.е. ряды вида
(21)
Заменой переменной 
ряд (21) сводится к уже рассмотренному ряду (19):
.
Функция , представимая степенным рядом (19) или (21), называется аналитической в интервале сходимости ряда.
Вся эта теория простых степенных рядов переносится на случай двойных степенных рядов.
§7. Область сходимости двойного степенного ряда.
Так же, как и для простых степенных рядов, в теории двойных степенных рядов решается задача о нахождении области сходимости ряда (18), т.е. множества 
тех точек плоскости, для которых ряд сходится. Как и в случае простых степенных рядов, имеет место основная
Лемма. Если ряд (18) сходится в некоторой точке 
, обе координаты которой отличны от нуля, то он абсолютно сходится во всех точках 
, удовлетворяющих неравенствам 
(т.е. во всем открытом прямоугольнике с центром в начале координат и с вершиной в точке 
).
Доказательство: вполне аналогично доказательству соответствующей леммы для простых степенных рядов. Из ограниченности членов ряда (18) при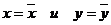 
имеем
,
так что
.
Поскольку ряд 
сходится, если только , то отсюда, признаку сравнения следует абсолютная сходимость ряда (18).
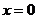Мы станем изучать в дальнейшем лишь такие ряды (18), для которых подобные точки существуют - другие ряды дл нас не представляют интереса. Заметим попутно, что всякий двойной степенной ряд сходится при и 
, т.е. в начале координат. И в то же время существуют двойные ряды, которые больше нигде не сходятся, т.е. расходятся, если 
. Примером такого ряда может служить двойной ряд
,
который расходится при любых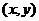 
, если , т.к. общий член ряда 
при 
, 
.
Характер доказанной леммы позволяет нам ограничиться рассмотрением лишь первого координатного угла. Полученные результаты по симметрии распространяются и на остальные углы.
Чтобы определить теперь область сходимости ряда (18) возьмем в первом угле луч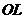 
, исходящий из начала под углом 
к оси 
.
Рассмотрим множество длин отрезков 
, где - точка сходимости ряда (18) и пусть 
- его точная верхняя граница.
Если хоть для одного луча 
, то в силу леммы, ряд (18) оказывается сходящимся (и притом - абсолютно) на всей плоскости, которая и играет роль области сходимости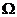 
.
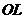Исключим теперь этот случай всюду сходящегося ряда (18). Тогда будет конечной функцией от и на каждом луче найдется пограничная точка 
, для которой 
. Она отделяет точки 
луча, в которых ряд (абсолютно) сходится от точек, где он расходится. В самой точке , смотря по случаю, может иметь место и сходимость и расходимость.
Если провести через вертикаль 
и горизонталь 
, то внутри прямоугольника 
ряд заведомо сходится, а внутри угла 
- заведомо расходится (по лемме!). Поэтому на новом луче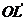 
, отвечающем какому-нибудь другому углу 
, вдоль 
будет сходимость, а вдоль 
- расходимость. Следовательно, пограничная точка 
на этом луче должна лежать между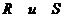 
. Отсюда легко усмотреть, что при изменении от 
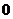до 
описывает в первом координатном угле непрерывную пограничную кривую.
Т.к. при уменьшении абсцисса 
точки не убивает, а ордината ее 
не возрастает, то обе имеют предельные значения при 
. Тогда, очевидно, имеет предельное значение и :
.
Если этот предел конечен, то точка 
стремится к некоторой предельной точке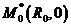 
на оси 
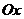. В противном же случае пограничная кривая имеет асимптотику, параллельную оси 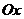(которая может совпадать и с самой осью 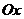).Все сказанное годится и для случая 
.
Замечание. Не следует, однако, думать, что предельная точка 
, о которой только что шла речь, необходимо совпадает с пограничной точкой 
на самой оси 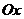. Точка может оказаться и правее (и даже лежать в бесконечности). Эта возможность не должна Вас удивлять, т. к. лемма и построенные на ней рассуждения относятся лишь к точкам вне координатных осей.
Дополним теперь построенную в первом координатном угле кривую симметричными ей (относительно обеих осей и начала координат) кривыми в остальных углах. Таким путем мы получим полную пограничную кривую, которая в существенном и определит интересующую нас “область сходимости” 
: в той части плоскости, которая извне ограничена этой кривой, ряд (18) сходится (и притом абсолютно), во внешней части плоскости ряд расходится (если не считать координатных осей), в точках же самой пограничной крив