Пусть двойной ряд

(22)
ограниченно сходится, т. е. существует такое число  , что
, что 

 где
где

(23)
Для  и
и  , удовлетворяющих неравенствам
, удовлетворяющих неравенствам


рассмотрим двойной степенной ряд

(24)
Теорема 1. Если ряд (22) ограниченно сходится, то ряд (24) абсолютно сходится для всех  и
и  таких, что
таких, что  , и имеет место равенство
, и имеет место равенство

Доказательство. Т.к.
 (25)
(25)
то  в силу ограниченной сходимости ряда (22). Следовательно, для
в силу ограниченной сходимости ряда (22). Следовательно, для 

т. е. ряд (24) абсолютно сходится. В силу (25),



 .
.
Сходимость ряда (22) означает, что для любого 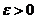
 натуральные
натуральные  и
и  такие, что
такие, что



где  - сумма ряда (22), причем, в силу ограниченной сходимости этого ряда,
- сумма ряда (22), причем, в силу ограниченной сходимости этого ряда,  Из очевидного тождества
Из очевидного тождества

имеем

откуда

 .
.
Поскольку  , то для
, то для 
 ,
,
 ,
,
 ,
,
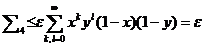 .
.
Следовательно,
 .
.
Из этого неравенства следует, что  и фиксированных
и фиксированных  и
и  найдутся числа
найдутся числа 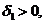
 такие, что при
такие, что при  и
и  будем иметь
будем иметь  . Отсюда следует, что
. Отсюда следует, что  .
.
Утверждение теоремы 1 можно обобщить, отказавшись от сходимости ряда (22) и ограничившись сходимостью некоторых средних от частных сумм этого ряда. Пусть

(26)
т. е.  - средние арифметические частных сумм ряда (22). Справедлива следующая
- средние арифметические частных сумм ряда (22). Справедлива следующая
Теорема 2. Если последовательность 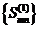 ограничена числом
ограничена числом  и существует предел
и существует предел  , то
, то  .
.
Доказательство. Из (26) имеем (см. (25)):
 ,
,  .
.
Из этих неравенств следует, что ряды
 ,
,  ,
, 
сходятся абсолютно для всех  .
.
Но тогда в силу равенства

(27)
имеем, применяя это равенство еще раз к ряду в правой части и учитывая (26)

(28)
Из (27) и (28) найдем
 .
.
Из существования предела  следует, что
следует, что


 (29)
(29)
а из условия ограниченности 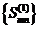 получим. Что
получим. Что  и, значит,
и, значит,

 .
.
В силу очевидного тождества

имеем

 ,
,
где  .
.
Суммы, стоящие в правой части этого равенства, оцениваются следующим образом
 ,
,
 ,
,
 ,
,
 .
.
Теперь получим оценку
 Если при фиксированных
Если при фиксированных  и
и  положить
положить  ,
,  ,
,  ,
,  , то
, то  Следовательно,
Следовательно,  .
.
Замечание. Рассмотрим величины:
 ,
,  , …,
, …,  .
.
Если существует число  такое, что
такое, что  , то последовательно получаются неравенства
, то последовательно получаются неравенства
 ;
;
 , …
, …
 ,
, 
 ,
,

из которых следует абсолютная сходимость для  ,
,  рядов
рядов

 ,
,  ,
, 

по теореме сравнения. Действительно,
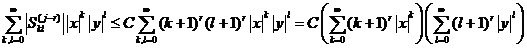 ,
,
А каждый из полученных справа степенных рядов сходится: первый при  , второй – при
, второй – при  , т. к. их радиус сходимости
, т. к. их радиус сходимости

Докажем теперь следующие обобщения теоремы 2.
Теорема 3. Если существует постоянная  такая, что
такая, что 
 и выполняется соотношение
и выполняется соотношение  , то
, то

Доказательство. Пусть полином  имеет вид
имеет вид
 (члены низшей степени)
(члены низшей степени)
и пусть равенство
 (30)
(30)
имеет место для всех натуральных  и
и  . Покажем, что в этом случае выполняется равенство
. Покажем, что в этом случае выполняется равенство 



Из очевидного равенства
 (31)
(31)
найдем:



 . (32)
. (32)
Это делается следующим образом. Умножая равенство (31) на  и суммируя по
и суммируя по  от 0 до
от 0 до  , получим:
, получим:



Далее, производя сдвижку индексов в последних трех суммах, получим:




На основании тождеств
 ,
,
 ,
,
 ,
,
подставляя вместо  ,
,  ,
,  их значения в выражения для
их значения в выражения для  , получим требуемое равенство (32).
, получим требуемое равенство (32).
Очевидно, что


 (члены низшей степени)]=
(члены низшей степени)]=
 ;
;
 ;
;





 ,
,
где  ,
,  - полиномы относительно
- полиномы относительно  и
и  более низших степеней.
более низших степеней.
В силу условия (30) имеем
 ;
;
 ;
;
 ;
;
 .
.
Из этих равенств и формулы (32) следует, что
 .
.
Теперь предположим, что  и покажем, что выполняется равенство (30).
и покажем, что выполняется равенство (30).
Рассмотрим полином

 (члены низшей степени).
(члены низшей степени).
Очевидно, что
 ,
, 
 ,
,
где  - фиксированное число.
- фиксированное число.
Для любого сколь угодно малого наперед заданного 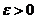 найдутся натуральные
найдутся натуральные  и
и  такие, что неравенство
такие, что неравенство

будет выполнятся для всех 
 . Т. к. из условий теоремы имеем
. Т. к. из условий теоремы имеем  , из предыдущего неравенства следует, что
, из предыдущего неравенства следует, что
 .
.
Далее,

где  .
.
Для этих сумм получаются следующие оценки:

 ;
;



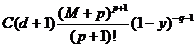 ;
;
 ;
;
 ;
;
С помощью этих оценок найдем



Теперь, при фиксированных  и
и  можно найти
можно найти 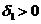 и
и  такие, что для всех
такие, что для всех 

 будем иметь
будем иметь

для всех 

 и, следовательно,
и, следовательно,
 .
.
В силу очевидного (и фактически доказанного выше при нахождении оценок сумм) равенства

из  следует соотношение (30). Поскольку (30) верно
следует соотношение (30). Поскольку (30) верно  , то полагая в (30)
, то полагая в (30)  , получим
, получим
 ,
,
ч. т. д.