Лабораторная работа № 13
Обработка двухмерных массивов с использованием указателей
Цель работы
1.1 Получение навыков в написании программ с использованием указателей.
1.2 Получение навыков программирования некоторых операций над матрицами с использованием указателей.
Техническое обеспечение
2.1 Персональная ЭВМ IBM PC/286 и более поздних моделей.
2.2 Клавиатура.
2.3 Дисплей.
2.4 Печатающее устройство.
Программное обеспечение
3.1 Операционная система MS DOS версия 5.0 и более поздние версии.
3.2 Система программирования Borland C++ версия 3.1 и более поздние версии.
Постановка задачи
Выполнить операции над матрицами согласно указанного варианта.
Содержание отчета
5.1. Тема и цель работы.
5.2. Схема алгоритма решения задачи.
5.3. Текст программы.
5.4. Результаты выполнения программы.
Общие сведения
Указатели на многомерные массивы
Многомерный массив в языке С – это массив массивов, т. е. Массив, элементами которого являются массивы. Например, двухмерный массив есть массив, элементы которого одномерные массивы
int arr [M][N];
Массив arr состоит из M элементов. Каждый элемент – одномерный массив размерностью N. В памяти массив arr расположен следующим образом:
| ... | Первый массив из N элем-тов | Второй массив из N элем-тов | ... | M - й массив из N элем-тов | ... |
Рассмотрим, как осуществлять доступ к элементам многомерного массива через указатель. Сделаем это на примере массива arr.
Объявим указатель и свяжем его с массивом arr
int *ptr;
ptr = &arr[0][0];
Необходимо получить доступ к элементу arr [ i ][ j ], или к j -му элементу i -й строки массива arr. Последовательно это вычисляется так:
адрес первого массива arr ptr
адрес j -го элемента i -й строки, ptr + i*N + j
т. е. элемента arr[i][j]
Пример.
/* Сложение двух матриц */
void add_matr(float *matr1, float matr2, int m, int n)
{
int i;
for (i = 0; i < m*n; i++)
*(matr1 + i) = *(matr1 + i) + *(matr2 + i);
out_matr(matr1, m, n);
}
Передача массивов в функции
Когда массив используется в качестве аргумента функции, передается только адрес массива, а не копия всего массива. При вызове функции с именем массива в функцию передается указатель на первый элемент массива. Параметр должен иметь тип, совместимый с указателем. Имеется три способа объявления параметра, предназначенного для получения указателя на массив. Во-первых, он может быть объявлен как массив:
#include <stdio.h>
void display (int num[10]);
int main (void)
{
int t[10], i;
for (i = 0; i < 10; i++) t[i] = i;
display (t);
return 0;
}
void display (int num[10])
{
int j;
for (j = 0; j < 10; j++) printf(“%d “, num[j]);
}
Второй способ состоит в объявлении параметра для указания на безразмерный массив, как показано ниже:
void display (int num[ ])
{
int j;
for (j = 0; j < 10; j++) printf(“%d “, num[j]);
}
И, наконец, третий способ, которым может быть объявлен num, - это наиболее типичный способ, применяемый при написании профессиональных программ, - через указатель, как показано ниже:
void display (int *num)
{
int j;
for (j = 0; j < 10; j++) printf(“%d “, num[j]);
}
Все три способа объявления параметра приводят к одинаковому результату – указателю.
Важно также понять, что при использовании массива в качестве аргумента функции происходит передача в функцию его адреса. Это означает, что код внутри функции действует и может изменить настоящее значение массива, используемого при вызове.
Некоторые операции над матрицами
Ввод матрицы обычно задается по строкам с помощью двух циклов. При использовании указателей это будет выглядеть следующим образом:
/* Ввод матрицы по строкам */
void input_matr (float *matr, int m, int n)
{
int i, j;
float b;
for (i = 0; i < m; i++) {
printf(“\nвведите элементы %d-й строки: “, i + 1);
for(j = 0; j < n; j++) {
scanf(“%f”, &b);
(matr + i*n + j) = b;
}
}
}
Вывод матрицы организуется построчно, как и ввод, с помощью двух циклов. При использовании указателей это будет выглядеть следующим образом:
/* Вывод матрицы по строкам *.
void out_matr(float *matr, int m, int n)
{
int i, j;
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++)
printf (“%.2f “, (matr + i*n + j));
printf(“\n”);
}
printf(“\n”);
}
Операции с константами сводятся к сложению или вычитанию элементов матрицы aij с константой, например х, или умножению aij * х или делению aij / х на константу.
Транспонированной матрицей называется матрица, у которой столбцы и строки меняются местами, т. е. из матрицы размера m ´ n получатся матрица размером n ´ m. Например, для матрицы А размером 3´4это:


Нетрудно заметить, что транспонирование матрицы реализуется с помощью соотношения  .
.
Произведением двух квадратных матриц А и В является третья матрица С, элементы которой вычисляются по формуле:
 .
.
Таким образом, элемент сij матрицы С = А×В есть сумма произведений элементов i -й строки матрицы А на соответствующие элементы i -го столбца матрицы В.

Методические указания
7.1 Ввод и вывод массива, а также операции над матрицами оформить в виде функций, не возвращающих значение.
7.2 При вводе, выводе и обработке матриц использовать указатели на массивы
Варианты заданий
1. Даны квадратные матрицы А и В порядка n. Получить матрицу С = А×В - В×А.
2. Дана квадратная матрица А порядка n. Получить матрицу А×В, где элементы матрицы В вычисляются по формуле:
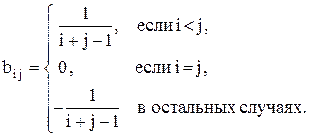
3. Даны квадратные матрицы А и В порядка n. Получить матрицу С = АТ - ВТ, где АТ и ВТ – транспонированные матрицы.
4. Даны квадратные матрицы А и В порядка n. Получить произведение А×ВТ
5. Даны квадратные матрицы А и В порядка n. Получить матрицу А2 + В2.
6. Даны квадратные матрицы А, В и С порядка n. Получить матрицу (А + В)× С.
7. Дана квадратная матрица А порядка n. Получить матрицу АТ × ВТ, где АТ – транспонированная матрица, а элементы матрицы В вычисляются по формуле:
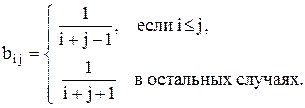
8. Даны квадратные матрицы А и В порядка n. Получить матрицу А ×(В – Е) + С, где Е – единичная матрица порядка n, а элементы матрицы С вычисляются по формуле:
 i, j = 1, 2, …, n.
i, j = 1, 2, …, n.
9. Дана матрицы А и В размера m´n. Получить матрицу АТ + ВТ, где АТ и ВТ – транспонированные матрицы.
10. Дана квадратная матрица А порядка m. Получить матрицы 0.5×(A + AT) и 0.5×(А – А Т), где АТ – транспонированная матрица.
11. Даны квадратные матрицы А и В порядка m. Получить матрицу АТ×В + А×ВТ, где АТ и ВТ – транспонированные матрицы.
12. Даны квадратные матрицы А и В порядка n. Получить матрицу С = АТ - В2, где АТ – транспонированная матрица.
13. Дана квадратная матрица А порядка n. Получить матрицу B порядка n, элементы которой вычисляются как разность между элементом aij и минимальным элементом i-й строки.
14. Дана квадратная матрица А порядка n. Получить матрицу B порядка n, элементы bij которой вычисляются как разность между максимальным элементом j-го столбца и элементом aij.