Лекция №16
Тема: «Изгиб»
Вопросы:
Понятие о деформации изгиба
Нормальные напряжения при чистом изгибе
Расчет балок на прочность по нормальным напряжениям
Понятие о деформации изгиба
Искривление оси бруса под действием внешней нагрузки называется изгибом. При изгибе в поперечном сечении возникают изгибающие моменты М, т.е. моменты, плоскость действия которых перпендикулярна плоскости сечения. Если изгибающие моменты являются единственным внутренним усилием, то изгиб называют чистым. Однако в большинстве случаев в сечениях бруса помимо изгибающего момента М возникают и поперечные силы Q. Такой изгиб называют поперечным.
Изгиб может быть прямым (плоским) или косым. Прямой изгиб происходит, если плоскость изгибающего момента проходит через одну из главных осей, косой изгиб - если не проходит.
Нормальные напряжения при чистом изгибе
Если на стержень нанести продольные и поперечные линии и подвергнуть его чистому изгибу, то продольные линии изогнутся по дугам окружностей, а поперечные линии 1-1 и 2-2 останутся прямыми, повернувшись на какой-то угол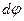 
(см. рис. 1).
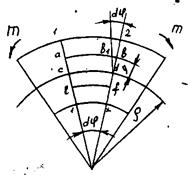
Рис. 1
В результате линия ab удлинится, а lf - укоротится, следовательно верхние волокна стержня испытывают растяжение, а нижние - сжатие. Линия cd, совпадающая с осью стержня сохранит прежнюю длину, т.е. не растягивается и не сжимается. Слой материала, лежащий на линии cd называют нейтральным слоем.
Из точки d проведем линию, параллельно линии 1-1. Образуемый ее угол с линией 2-2 будет 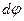. Линия ab удлинилась на дугу 
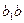, длину которой можно определить по формуле:
.
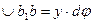Относительная деформация линии ab будет равна:
,
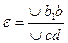но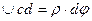 
.
|
|
В результате получим:
.
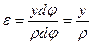Согласно закона Гука:
,
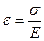поэтому:
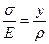или 
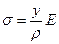(1)
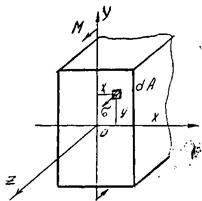
Рис. 2
Рассмотрим поперечное сечение стержня (рис. 2). В нем будет возникать только одно внутреннее усилие - изгибающий момент М, равный внешнему моменту m.
M = m
Установим положение нейтрального слоя, от которого отмеряется расстояние Y. Для этого воспользуемся тем. что равнодействующая элементарных нормальных сил s dA при чистом изгибе должна быть равна нулю:
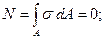
или подставив формулу (1), получим:
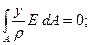
Так как множитель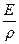 
величина постоянная, то его можно вынести за знак интеграла и сократить, получим:
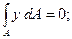
Полученный интеграл представляет собой статический момент сечения Sx. Поскольку он равен нулю, то ось X проходит через центр тяжести сечения.
“При чистом изгибе нейтральная ось проходит через центр тяжести сечения”.
Элементарные силы, возникающие на элементарных площадках dA, будут вызывать элементарные моменты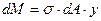 
. Сумма элементарных моментов в сечении должна составить изгибающий момент М.
.
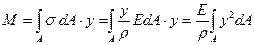Интеграл, входящий в это выражение представляет собой момент инерции сечения относительно оси X (см. формулу (4), лекция 12):
;
поэтому:
;
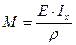откуда находим кривизну нейтрального слоя:
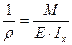(2)
Подставляя это выражение в формулу (1), окончательно получим:
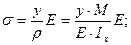
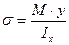(3)
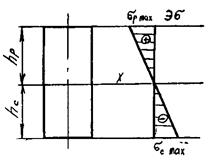
Рис. 3
Из формулы видно, что напряжение прямо пропорционально расстоянию от нейтрального слоя Y. Для точек, находящихся на нейтральном слое, y=0 и x=0. Наибольшие напряжения будут возникать в точках, наиболее удаленных от нейтрального слоя.
Максимальные напряжения будут равны:
;
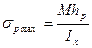(4)
;
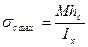где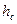 
и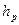 
- соответственно высота сжатой и растянутой зоны.
|
|
Эпюра напряжений будет иметь вид, показанный на рис. 3.
Если = =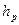 
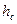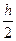, то:
,
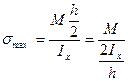Обозначив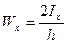 
, (5)
называемый осевым моментом сопротивления, получим:
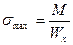(6)
Формула (3) и полученная из нее (6), выведенные при чистом изгибе, применимы и при поперечном изгибе.
Возьмем сумму элементарных моментов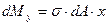 
относительно оси Y (см. рис. 2). Он должен быть равен нулю, так как стержень относительно оси Y не изгибается.
.
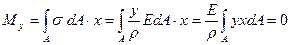Интеграл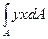 
представляет собой центробежный момент инерции 
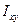и он равен нулю. Мы отмечали, что если 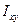= 0, то ось главная. Следовательно, при плоском изгибе нейтральная ось является центральной и главной.
Расчет балок на прочность по нормальным напряжениям
Как уже отмечалось, пластичные материалы имеют одинаковую прочность на растяжение и сжатие. Поэтому профили балок из пластичных материалов делают симметричными относительно центральной оси. Условие прочности для них:
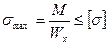, (7)
где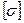 
- допускаемое напряжение материала на растяжение.
Из условия прочности можно решить следующие три задачи:
1. Проверить на прочность. Прочность обеспечена, если максимальное напряжение меньше или равно допускаемому напряжению.
2. Подобрать сечение. Из условия прочности получим:
.
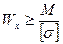Значения Wx находят по формуле (5).
Для прямоугольного сечения:
;
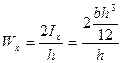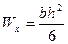(8)
Задавшись высотой или шириной сечения, можно определить второй размер.
Для круглого сечения h=d
;
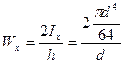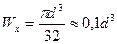; (9)
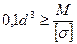
или (10)
Для двутавра, швеллера и уголков приводятся таблицы (в конце учебников и в справочниках), в которых в зависимости от номера профиля дается значение Wx. По требуемому значению Wx выбирается нужный номер профиля.
|
|
3. Определить эксплуатационные способности. Из условия прочности получим:
.
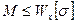Балки из хрупких материалов изготавливают несимметричными относительно нейтрального слоя, так как хрупкий материал гораздо лучше сопротивляется сжатию, чем растяжению. В этом случае составляют два условия прочности:
;
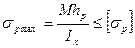(11)
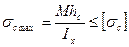
и решают те же три задачи, что и для балки из пластичного материала.