Пример.
Метод хорд = Метод ложного положения = метод линейной интерполяции = метод пропорциональных частей
Пусть задано уравнение
f(x)=0 (1),
где f(x) - определенная и непрерывная на отрезке [a,b] функция.
Требуется найти корень уравнения x с заданной степенью точности e.
1. Пусть функция непрерывна на отрезке [a,b], 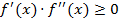 , B- неподвижная точка, x0=a.
, B- неподвижная точка, x0=a.
| А |
| B |
| a=x0 |
| b |
| y |
| x |
| x1 |
| x2 |
| x |
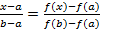 -уравнение секущей.
-уравнение секущей.
Найдем точку пересечения с осью 0x (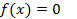 ). Тогда
). Тогда 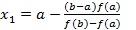 , или
, или
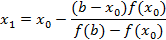
Продолжая процесс, получим итерационную формулу
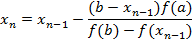
2. Пусть функция непрерывна на отрезке [a,b], 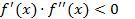 , А- неподвижная точка, x0=b.
, А- неподвижная точка, x0=b.
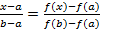 -уравнение секущей.
-уравнение секущей.
Найдем точку пересечения с осью 0x (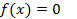 ). Тогда
). Тогда 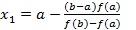 , или
, или
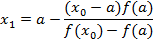
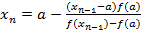 , или
, или 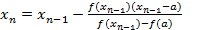
Метод Ньютона (метод касательных) нахождения корней
Пусть задано уравнение
f(x)=0 (1),
где f(x) - определенная и непрерывная на отрезке [a,b] функция.
Требуется найти корень уравнения x с заданной степенью точности e.
| y |
| x |
| a |
| b=x0 |
| x1 |
| x2 |
1. Рассмотрим касательную к кривой y=f(x) в точке x0. Она задается уравнением 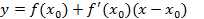 . Пересечение с осью 0x происходит при y=0.
. Пересечение с осью 0x происходит при y=0.
Тогда 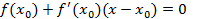 , или
, или 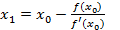 .
.
Продолжая процесс, получим рекуррентную формулу 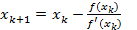 .
.
Теорема. Если функция является непрерывной вместе со своей второй производной на отрезке [a,b] и на концах отрезка функция имеет разные знаки, причем вторая производная на этом отрезке не меняет знака, то уравнение f(x)=0 имеет единственный корень x.
Дано: f(x)ÎС2[a,b], f(a)×f(b)<0, 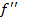 не меняет знака на отрезке [a,b].
не меняет знака на отрезке [a,b].
Доказать, что уравнение f(x)=0 имеет единственный корень x.
Доказательство. Так как функция непрерывна и на концах отрезка имеет разные знаки, то по следствию теоремы Вейерштрасса она имеет не менее одного корня.
Покажем, что корень - единственный. Предположим, что уравнение имеет два различных корня на отрезке [a,b]: x1 ¹x2. Это означает, что f(x1)= f(x2)=0. Тогда по теореме Ролля (следствие теоремы Лагранжа) существует такая точка cÎ[x1, x2], что 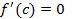 .
.
Рассмотрим случай, когда 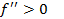 , то есть
, то есть 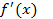 - возрастает на отрезке [a,b] и
- возрастает на отрезке [a,b] и 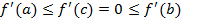 . Тогда на отрезке [a,c] функция f убывает и f(a)>f(x1)=0; на отрезке [c,b] функция f возрастает и f(b)>f(x2)=0. Оба конца отрезка оказались положительны, что противоречит условию теоремы. Противоречие возникло из предположения о том, что уравнение имеет два различных корня на отрезке [a,b]. Значит, корень единственный.
. Тогда на отрезке [a,c] функция f убывает и f(a)>f(x1)=0; на отрезке [c,b] функция f возрастает и f(b)>f(x2)=0. Оба конца отрезка оказались положительны, что противоречит условию теоремы. Противоречие возникло из предположения о том, что уравнение имеет два различных корня на отрезке [a,b]. Значит, корень единственный.
Алгоритм метода:
1. Отделяем корень.
2. Определяем знак второй производной: 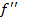 .
.
3. Выбираем в качестве 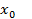 тот конец отрезка [a,b], знак функции f в котором бы совпадал со знаком
тот конец отрезка [a,b], знак функции f в котором бы совпадал со знаком 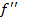 .
.
4. Применяем формулу 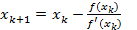 .
.
Оценим погрешность k-ого приближения метода Ньютона. По формуле Тейлора
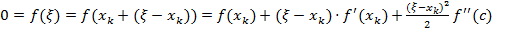 , сÎ[x;xk].
, сÎ[x;xk].
Поделим обе части равенства на 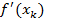 .
.
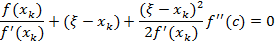
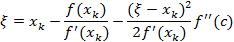
Из формулы Ньютона 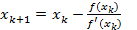 , поэтому
, поэтому 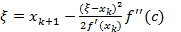 .
.
Обозначим 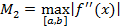 ,
, 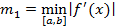 . Тогда
. Тогда
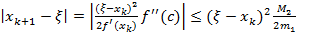 .
.
Обозначим 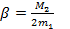 . Тогда
. Тогда
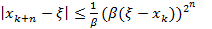 ,
, 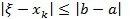 и
и
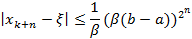
Если 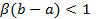 , то последовательность значений, полученных по методу Ньютона ограничена сверху сходящейся геометрической прогрессией.
, то последовательность значений, полученных по методу Ньютона ограничена сверху сходящейся геометрической прогрессией.
По свойствам предела последовательности если последовательность возрастает и ограничена сверху, то у неё есть предел; если последовательность убывает и ограничена снизу, то у неё также есть предел. Последовательность значений, полученных по методу Ньютона ограничена сходящейся геометрической прогрессией и одним из концов отрезка [a,b], следовательно, она сходится, причем её предел является корнем уравнения 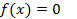 .
.
Пример.
Решение систем нелинейных уравнений методом Ньютона.
Пусть 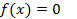 Û
Û 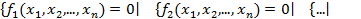 , где
, где 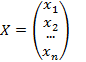 ,
, 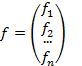 .
.
Предположим, что существует решение 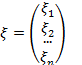 и
и 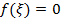 .
.
Пусть 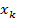 -некоторое приближение x и
-некоторое приближение x и 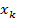 +dk=x. Разложим в ряд
+dk=x. Разложим в ряд 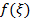 . Разложим в ряд Тейлора
. Разложим в ряд Тейлора 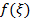 .
.
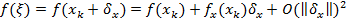
Здесь 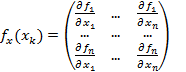 -якобиан функции f(X).
-якобиан функции f(X).
Если пренебречь 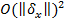 и учесть, что
и учесть, что 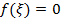 , то
, то
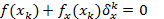 Þ
Þ 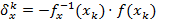 .
.
Пусть согласно новому методу 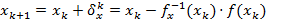 .
.
Тогда 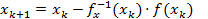 .
.
Алгоритм метода:
1. Выбираем приближенно 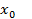 (найдено
(найдено 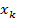 ).
).
2. Находим 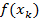 ,
, 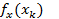
3. Решаем СЛАУ 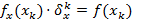 либо находим
либо находим 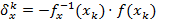 .
.
4. Находим 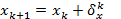 .
.
Теорема. Для того, чтобы у системы 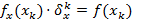 существовало, и притом единственное решение
существовало, и притом единственное решение 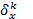 , необходимо и достаточно, чтобы определитель матрицы Якоби
, необходимо и достаточно, чтобы определитель матрицы Якоби
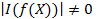 .
.
Пусть имеется некоторая точка X в окрестности x решения системы (1). Пусть функция f в окрестности  1) является гладкой в том смысле, что существуют производные функции f до второго порядка включительно такие, что
1) является гладкой в том смысле, что существуют производные функции f до второго порядка включительно такие, что 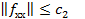 ; 2) матрица Якоби f(X) равномерно невырождена, то есть
; 2) матрица Якоби f(X) равномерно невырождена, то есть 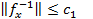 .
.
Тогда при достаточно близком значении X алгоритм метода Ньютона квадратично сходится к решению системы уравнений x.
Доказательство. Покажем, что 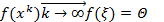 . Проследим за эволюцией невязки
. Проследим за эволюцией невязки 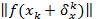 .
.
1) 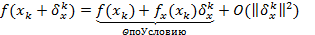 ;
;
2) 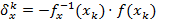 .
.
3) Рассмотрим 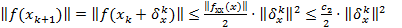
4) 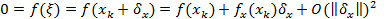 Þ
Þ
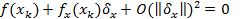 Þ
Þ 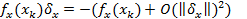
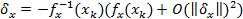
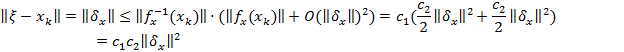
Пример
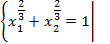
Решение систем линейных алгебраических уравнений (СЛАУ)
Рассмотрим систему линейных алгебраических уравнений:
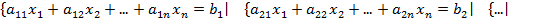 (1)
(1)
Выпишем матрицу коэффициентов при неизвестных:
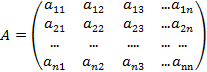
и два вектора
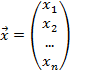 и
и 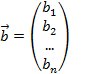
Тогда систему (1) можно записать в матричной форме 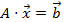
Квадратная матрица А называется невырожденной, или неособенной, если det A=|A|¹0.
Если матрица A коэффициентов при неизвестных СЛАУ невырождена, то система имеет единственное решение.
| СЛАУ |
| Совместная (существует хотя бы одно решение) |
| Несовместная (противоречивая) не имеет решений |
| Определенная (единственное решение |
| Неопределенная (более одного решения) |
Методы решения линейных систем можно разбить на две группы:
точные (прямые) и приближенные.
1. Точные алгоритмы позволяют получить решение за конечное число арифметических действий. К ним относятся: метод Гаусса, метод Крамера, метод прогонки, метод квадратных корней.
2. Приближенные методы: метод простой итерации, метод Зейделя, метод релаксации.
1. Точные методы.
Метод Гаусса (схема единственного деления).
Существуют различные вычислительные схемы, реализующие этот метод. Рассмотрим схему единственного деления. Предположим, что 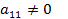 (в противном случае меняем строки №1 и №k местами,
(в противном случае меняем строки №1 и №k местами, 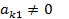 , либо столбцы №1 и №k местами,
, либо столбцы №1 и №k местами, 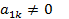 ). В полученной системе поделим первое уравнение на
). В полученной системе поделим первое уравнение на 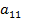 . Полученное уравнение умножим сначала на
. Полученное уравнение умножим сначала на 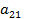 , затем на
, затем на 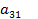 и
и 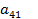 результаты соответственно вычитаются из 2, 3, и 4 уравнений. Тогда получим новую систему, содержащую 3 уравнения с 3 неизвестными.
результаты соответственно вычитаются из 2, 3, и 4 уравнений. Тогда получим новую систему, содержащую 3 уравнения с 3 неизвестными.
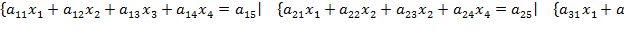
Þ 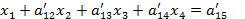
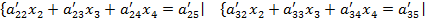
Þ 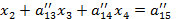
Поступая аналогично с полученной системой, мы исключим неизвестную 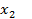 .
.
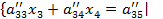
Þ 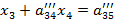
Аналогично из последней системы исключаем 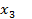 .
.
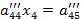
В результате исходная система (1) может быть заменена равносильной системой с треугольной матрицей. Приведение системы к системе с треугольной матрице называется прямым ходом, определение неизвестных 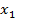 ,
, 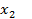 ,
, 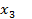 ,
, 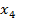 обратным ходом.
обратным ходом.
| Номер раздела | i | ai1 | ai2 | ai3 | ai4 | ai5 | ai6= ai1+ ai2+ ai3+ ai4+ ai5 (Сумма) |
| I | a11 | a22 | a13 | a14 | a15 | a16 | |
| a21 | a22 | a23 | a24 | a25 | a26 | ||
| a31 | a32 | a33 | a34 | a35 | a36 | ||
| a41 | a42 | a43 | a44 | a45 | a46 | ||
| b12 | b13 | b14 | b15 | b16= a16/ a11=1+ b12+ b13+ b14+ b15 | |||
| II | 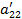
| 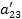
| 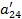
| 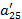
| 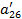
| ||
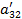
| 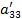
| 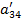
| 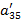
| 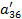
| |||
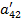
| 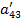
| 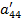
| 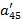
| 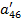
| |||
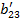
| 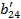
| 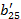
| 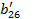 = = 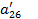 / / 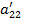 =1+ =1+ 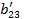 + + 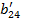 + + 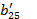
| ||||
| III | 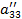
| 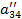
| 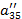
| 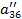
| |||
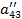
| 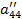
| 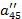
| 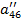
| ||||
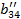
| 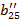
| 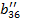 = = 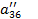 / / 
| |||||
| IV | 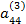
| 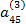
| 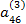
| ||||
| x4 | 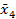
| ||||||
| x3 | 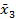
| ||||||
| x2 | 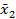
| ||||||
| x1 | 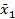
|
Порядок заполнения таблицы.
Прямой ход
1. Записываем коэффициенты данной системы в четырех строках и 5 столбцах раздела I
2. Суммируем все коэффициенты по строке и записываем их в столбце «Сумма» (столбец контроля).
3. Делим все числа 1 строки на a11 и результат записываем в 5 строку раздела I.
4. Вычисляем сумму b1j, j=1..5, если вычисления ведутся с постоянным знаком после запятой, то числа b16 и 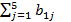 не должны отличаться более, чем на 1 последнего разряда.
не должны отличаться более, чем на 1 последнего разряда.
5. Вычисляем коэффициенты 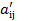 и результаты записываем в первые 3 строки раздела II.
и результаты записываем в первые 3 строки раздела II.
6. Делаем проверку. Сумма элементов каждой строки раздела II (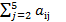 )должна совпадать с
)должна совпадать с 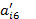 .
.
7. Делим элементы строки 2 раздела II на 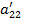 , и результаты записываем в последнюю строку раздела II.
, и результаты записываем в последнюю строку раздела II.
8. Делаем соответствующую проверку.
9. Аналогично заполняем и проверяем III, IV разделы.
Обратный ход.
1. В разделе V записываем 1 (как показано в схеме).
2. Вычисляем 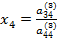 .
.
3.Для вычисления x3, x2, и x1 используются последние строчки разделов 3, 2, 1, содержащие 1.
Аналогично проводится обратный ход в контрольной схеме. Исходная система и контрольная система имеет одну и ту же матрицу коэффициентов при неизвестных и отличаются только столбцами свободных членов.
Если 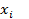 - решение исходной системы, а
- решение исходной системы, а 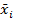 - решение контрольной системы, то
- решение контрольной системы, то 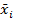 =
= 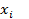 +1.
+1.
Последний контроль осуществляется только с помощью столбца «Сумма».
Вычисление определителя.
С помощью схемы единственного деления можно вычислить определитель матрицы A. Пусть 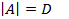 Операции по исключению
Операции по исключению 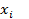 определитель не изменяют, изменяет только деление на a11,
определитель не изменяют, изменяет только деление на a11, 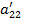 ,
,  ,
, 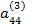 - определитель изменится и станет равным
- определитель изменится и станет равным 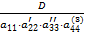 . С другой стороны, определитель треугольной матрицы равен 1. Тогда
. С другой стороны, определитель треугольной матрицы равен 1. Тогда  и
и  .
.
Обращение матрицы.
Пусть дана матрица A.
Определение. Матрица A-1 называется обратной по отношению к матрице A, если 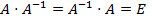 , где E- единичная матрица.
, где E- единичная матрица.
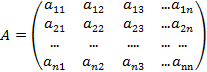
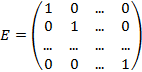
Определение. Квадратная матрица A называется неособенной (невырожденной), если detA=|A|¹0.
Теорема. Всякая невырожденная матрица имеет обратную.
Рассмотрим случай отыскания матрицы, обратной матрице A, размерностью 4´4.
 ,
, 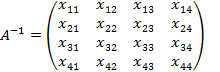 ,
, 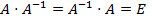
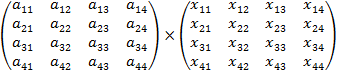 =
= 
Данную систему можно представить в виде совокупности четырех СЛУ:
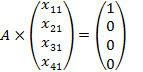 ,
, 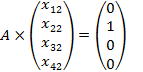 ,
, 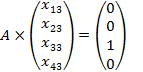 ,
, 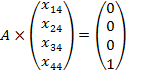 .
.
Таким образом, предстоит решить одновременно четыре СЛУ, имеющих одну и ту же матрицу коэффициентов при неизвестных и отличающихся только столбцами свободных членов.
Используем компактную схему Гаусса. В ней вместо столбца свободных членов записываем единичную матрицу, контрольный столбец рассчитывается аналогично.
Метод Крамера.
Алгоритм:
1. Вычисляем определитель матрицы A.
2. Для того, чтобы найти компоненту решения xi, необходимо поделить определитель матрицы, полученной путем замены i- го столбца столбцом свободных членов на определитель матрицы А.
Доказательство: см. курс алгебры.
Приближенные методы.
1. Неподвижная точка оператора.
Определение. Операторºфункция, в общем случае отображение пространства в себя называется оператором; функционал f: (M,r)®(R, r1).
Определение. Множество М называется линейным пространством, если 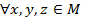 выполняются следующие аксиомы:
выполняются следующие аксиомы:
1. x+y=y+x
2. (x+y)+z=x+(y+z) ассоциативность слож
3. ($ 0ÎM) (x+0=0+x=x).
4. "xÎM ($ -xÎM) x+(-x)=0
5. 1×x=x
6. " l, m ÎR (lm)x=l(mx) ассоциативность умн
7. " l, m ÎR l (x+y)= x+ly; (l+m)x=lx+mx
Определение. Пусть задан оператор f: М®M. Тогда точка a называется неподвижной точкой оператора f, если f(a)=a.
Примеры неподвижных точек: корень уравнения, тождественное преобразование – все точки неподвижные; поворот 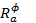 ; симметрия Sl относительно прямой l, l- неподвижная точка.
; симметрия Sl относительно прямой l, l- неподвижная точка.
Определение. Пусть дан оператор f: М®M, на множестве М введена метрика r. Тогда f есть оператор сжатия, или сжимающееся отображение, если ($a) (0<a<1 Þ ("xÎM) ("yÎM) (r(f(x),f(y))£a ×r(x,y))
Определение. Последовательность точек 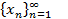 метрического пространства (M,r) называется фундаментальной, если она удовлетворяет условию Коши:
метрического пространства (M,r) называется фундаментальной, если она удовлетворяет условию Коши:
для любого 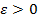 существует такое натуральное n0, что r(xn,xm)<e для всех n, m>n0.
существует такое натуральное n0, что r(xn,xm)<e для всех n, m>n0.
Определение. Метрическое пространство называется полным, если в нем любая фундаментальная последовательность сходится.
Теорема Банаха. Достаточный признак существования неподвижной точки.
Пусть (M,r) - полное метрическое пространство. В нем задан оператор f: М®M, f - оператор сжатия. Тогда 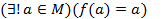 .
.
Доказательство. Возьмем произвольную точку x0ÎM. Рассмотрим последовательность 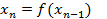 и покажем, что:
и покажем, что:
1) 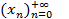 -сходящаяся последовательность. Обозначим
-сходящаяся последовательность. Обозначим 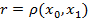 . Тогда
. Тогда 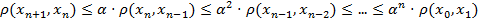
Найдем такое n0, чтобы выполнялось неравенство 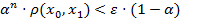 .
.
Тогда 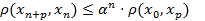
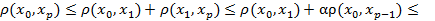
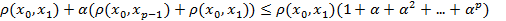 =
=
= 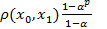
и 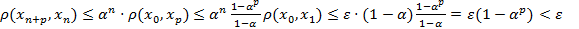
Получили:
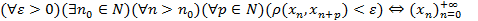 -фундаментальная последовательность, а значит, она сходится к некоторой точке a.
-фундаментальная последовательность, а значит, она сходится к некоторой точке a.
2) Покажем, что a - неподвижная.
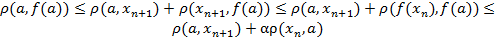
В правой части перейдем к пределу при n®¥.
Тогда
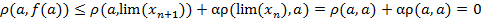
Таким образом,
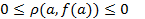 ®
® 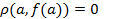 и
и 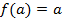
что и требовалось доказать.
Аналог теоремы Банаха.
Пусть (M, r)- линейное полное метрическое пространство, f - некоторый линейный оператор, 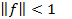 . Тогда существует, и притом единственная неподвижная точка оператора f.
. Тогда существует, и притом единственная неподвижная точка оператора f. 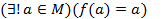 .
.
Доказательство. 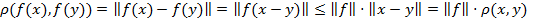
Таким образом, f - сжимающееся отображение.
Замечание 1.
Определение. Нормой оператора A в нормированном пространстве M называется
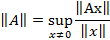
Норма оператора A согласована с нормой, введенной в пространстве M.
Следствие. 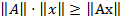 .
.
Погрешность.
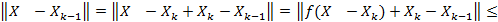
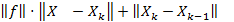 .
.
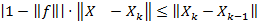 Þ
Þ 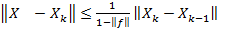 Þ
Þ
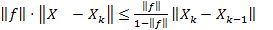 ;
; 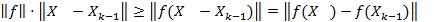 Þ
Þ
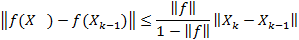
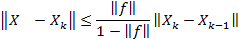
Замечание 2.
Пусть A-матричный оператор, т.е. A- матрица, 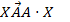 .
.
Тогда в качестве нормы матричного оператора можно выбрать следующие выражения:
1) 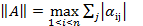 ;
;
2) 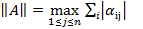 ;
;
3) 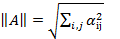 ;
;
Метод простой итерации для СЛУ
Пусть дана некоторая СЛУ. Её необходимо привести к виду X=A×X+B, или 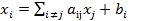 ,
, 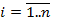 . Если одна из вышеперечисленных норм окажется меньше 1, то итерационный процесс сходится (на основании теоремы Банаха).
. Если одна из вышеперечисленных норм окажется меньше 1, то итерационный процесс сходится (на основании теоремы Банаха).
Метод Якоби.
Пусть необходимо решить систему вида 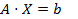 . Представим A=L+D+R, где D - диагональная матрица, L и R - соответственно левая и правая строго треугольные матрицы (т.е. с нулевой диагональю). Тогда
. Представим A=L+D+R, где D - диагональная матрица, L и R - соответственно левая и правая строго треугольные матрицы (т.е. с нулевой диагональю). Тогда 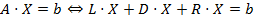 Û Û
Û Û 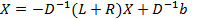 . Пусть
. Пусть 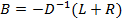 и
и 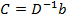 . Тогда
. Тогда 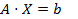 Û
Û 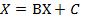 . Основанный на таком приведении метод простой итерации называется методом Якоби.
. Основанный на таком приведении метод простой итерации называется методом Якоби.
Определение. Диагональное преобладание означает, что 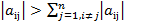 .
.
Теорема. В случае диагонального преобладания в матрице А системы метод Якоби сходится.
Определение 1. Пусть дана матрица А. Рассмотрим уравнение AX=lX. Тогда X¹0 называется собственным вектором матрицы А или собственным вектором данного линейного преобразования, а число l называется собственным значением.
Определение 2. Уравнение вида называется характеристическим уравнением матрицы А. Из этого уравнения находятся собственные числа (значения) l.
Теорема. Для сходимости метода простой итерации 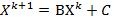 при любом начальном векторе
при любом начальном векторе 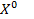 к решению
к решению  системы
системы 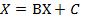 необходимо и достаточно, чтобы все собственные числа матрицы B были по модулю меньше 1.
необходимо и достаточно, чтобы все собственные числа матрицы B были по модулю меньше 1.
Метод Зейделя.
Итерационный процесс для метода Зейделя можно представить следующей последовательностью:
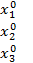 ®
® 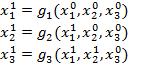 ®
® 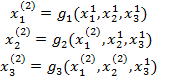
В связи с такой интерпретацией метод Зейделя называют методом последовательных смещений, а МПИ - одновременных смещений.
Пусть необходимо решить систему вида 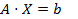 . Представим A=L+D+R, где D - диагональная матрица, L и R - соответственно левая и правая строго треугольные матрицы (т.е. с нулевой диагональю). Тогда
. Представим A=L+D+R, где D - диагональная матрица, L и R - соответственно левая и правая строго треугольные матрицы (т.е. с нулевой диагональю). Тогда 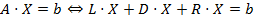 .
.
Тогда метод Зейделя есть 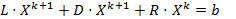 Û
Û 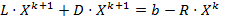 Û
Û 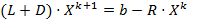 Û
Û 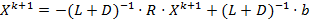 , что есть метод простой итерации (при условии, что L+D -обратима). Поэтому можно переформулировать ряд утверждений, справедливых для МПИ.
, что есть метод простой итерации (при условии, что L+D -обратима). Поэтому можно переформулировать ряд утверждений, справедливых для МПИ.
Теорема. Для сходимости метода Зейделя необходимо и достаточно, чтобы все корни уравнения
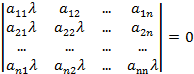
были по модулю меньше 1.
Доказательство. det((L+D)l+R)=0 Û 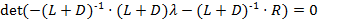 Û
Û
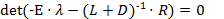 , где
, где 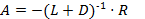 - матрица коэффициентов при неизвестных для МПИ, аналогичного методу Зейделя. Что и требовалось доказать.
- матрица коэффициентов при неизвестных для МПИ, аналогичного методу Зейделя. Что и требовалось доказать.
Теорема. Пусть 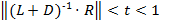 . Тогда при любом начальном векторе
. Тогда при любом начальном векторе 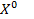 метод Зейделя сходится к решению
метод Зейделя сходится к решению  и справедливы оценки погрешности:
и справедливы оценки погрешности:
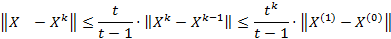
Доказательство. Метод Зейделя равносилен МПИ при 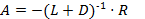 , а для него справедливы указанные оценки.
, а для него справедливы указанные оценки.
Определение. Матрица А называется симметричной тогда и только тогда, когда 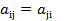 , j,i=
, j,i= 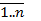 .
.
Определение. Линейный оператор А называется:
1) положительным, если 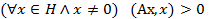
2) положительно определенным, если 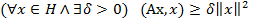
3) неотрицательным, если 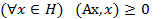
Определение. Система 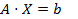 называется нормальной, если матрица А- симметричная положительно определенная.
называется нормальной, если матрица А- симметричная положительно определенная.
Теорема. Для существования единственного решения системы 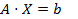 и сходимости метода Зейделя достаточно выполнения хотя бы одного из двух условий:
и сходимости метода Зейделя достаточно выполнения хотя бы одного из двух условий:
1) матрица А -нормальная;
2) 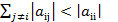 , i =
, i = 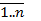 (диагональное преобладание)
(диагональное преобладание)
Замечание. Для применения этой теоремы необходимо, чтобы диагональные элементы матрицы А 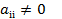 . Каждое i-ое уравнение делится на
. Каждое i-ое уравнение делится на 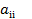 . Все неизвестные, кроме
. Все неизвестные, кроме 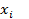 , переносятся вправо и переходим к эквивалентной системе X=CX+D, где
, переносятся вправо и переходим к эквивалентной системе X=CX+D, где 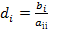 ,
, 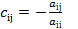 при j¹i; cij=0 при j=i
при j¹i; cij=0 при j=i
Доказательство.
1) Пусть матрица А -нормальная. Покажем, что процесс Зейделя сходится. Для этого убедимся, что собственные значения матрицы 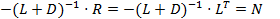 по модулю меньше 1.
по модулю меньше 1.
Лемма. Если A- симметричная матрица, то L=RT и R=LT.(ПРОВЕРИТЬ!)
Пусть 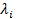 и
и 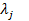 -собственные значения матрицы N, а
-собственные значения матрицы N, а 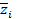 и
и 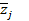 -соответствующие им собственные векторы. Тогда
-соответствующие им собственные векторы. Тогда 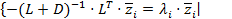 Þ
Þ 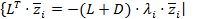 Þ
Þ 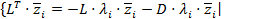
1) Рассмотрим скалярные произведения 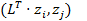 и
и 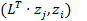 .
.
Они будут представляться в виде 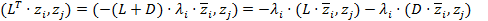 I
I
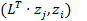 =
= 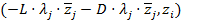 =
= 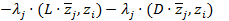 II
II
2) Учтем, что из коммутативности скалярных произведений и симметричности матрицы A следует: 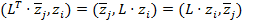
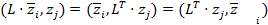
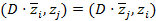
3) Из II имеем 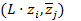 =
= 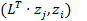 =
= 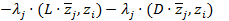 = =
= = 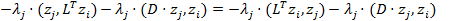
Þ 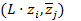 =
= 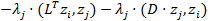 Ú.
Ú.
4) Тогда из I и последнего полученного равенства имеем систему:
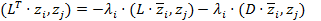 I
I
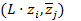 =
= 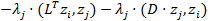 Ú
Ú
5) Система равносильна следующей системе:
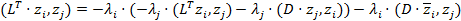
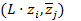 =
= 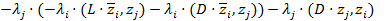
Откуда
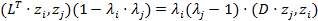
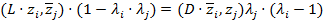
и
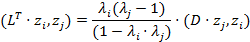
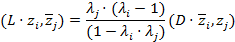
6) Тогда
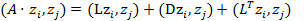 =
= 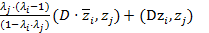 +
+ 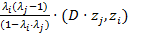 =
= 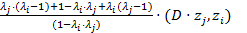 =
=
= 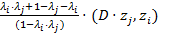 =
= 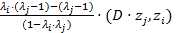 =
= 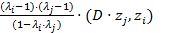
Положим здесь i=j, тогда найдем: 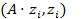 =
= 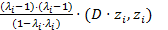 =
= 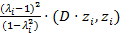
Так как A - положительно определенная, то 1) 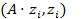 >0; 2) диагональные элементы матрицы A положительны, то есть
>0; 2) диагональные элементы матрицы A положительны, то есть 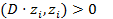 . Значит, обе части равенства положительны;
. Значит, обе части равенства положительны; 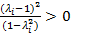 ;
; 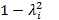 >0 и
>0 и 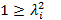 . Откуда
. Откуда 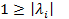 .
.
Заметим, что 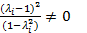 , так как если
, так как если 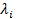 =1, то найдется
=1, то найдется 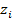 , такое, что
, такое, что 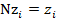 и
и 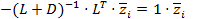 Û
Û 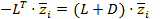 Û
Û 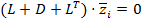 Û
Û 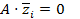 Û
Û 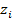 =q.
=q.
Таким образом, 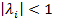 , что и требовалось доказать.
, что и требовалось доказать.
2) Покажем, что при диагональном преобладании метод Зейделя сходится. Для этого сравним процесс Зейделя с методом простой итерации и убедимся, что процесс Зейделя сходится быстрее, чем МПИ.
Пусть
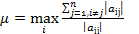 (норма). В силу диагонального преобладания m<1. Обозначим
(норма). В силу диагонального преобладания m<1. Обозначим 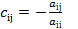 ,
, 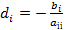 . Тогда процесс Зейделя равносилен методу простой итерации с вычислительной схемой
. Тогда процесс Зейделя равносилен методу простой итерации с вычислительной схемой 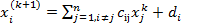 , а вычислительная схема метода Зейделя
, а вычислительная схема метода Зейделя 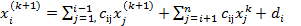 .
.
Для МПИ верно:
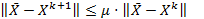 . Введем обозначения:
. Введем обозначения: 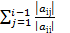 =
= 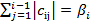 ,
, 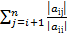 =
= 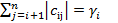 ,
, 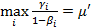 .
.
Покажем, что разность между точным решением и (k+1) приближением по методу Зейделя оценивается с помощью неравенства:
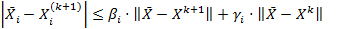 (покоординатная оценка)
(покоординатная оценка)
Действительно,
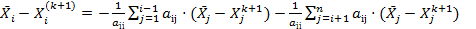 Þ
Þ
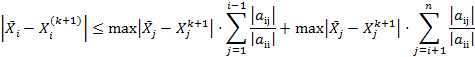
Среди номеров найдется такой номер iÎ[1,n], что