Метод наискорейшего (градиентного) спуска

Пусть необходимо решить систему уравнений:

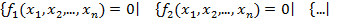(1)

Введем обозначения: 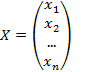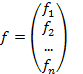. Тогда систему (1) в матричной форме можно записать как f(X)=Q.

Данная система эквивалентна одному уравнению 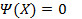, где

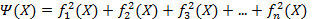(2)

Решениями этого уравнения являются точки нулевых минимумов функции .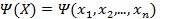

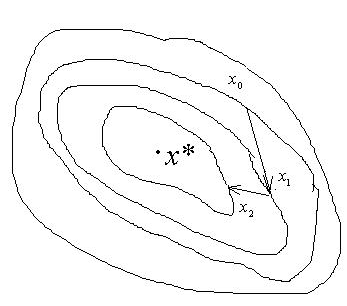
Пусть 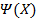- дважды непрерывно дифференцируемая функция в области, содержащей изолированное решение x^*, в окрестности которого поверхности уровня функции 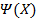имеют вид вложенных колец, внутри которых точка x^*.

Возьмем произвольно начальное приближение .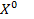

Замечание.

Градиент (от лат. gradiens, род. падеж gradientis — шагающий) — характеристика, показывающая направление наискорейшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой. Например, если взять высоту поверхности Земли над уровнем моря (2-мерное пространство), то её градиент в каждой точке поверхности будет показывать «в горку».

Как видно из объяснения, градиент является векторной функцией, а величина, которую он характеризует — функцией скалярной.

Формально, для случая трёхмерного пространства, градиентом называется векторная функция с компонентами 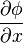, , 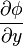, 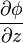где φ — некоторая скалярная функция координат x, y, z.

Если 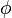— функция n переменных 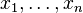, то её градиентом будет n-мерный вектор

,

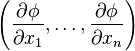компоненты которого равны частным производным 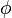по всем её аргументам.

Градиент обозначается 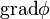или, с использованием оператора набла, .

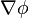Из определения градиента следует, что:

 

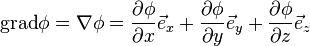
Найдем такое число 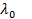, чтобы 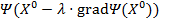было минимальным (здесь 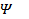зависит только от одной переменной - ). Для этого найдем первую производную 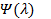и приравняем её к нулю:

.

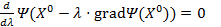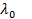( -минимальный неотрицательный корень из всех корней данного уравнения!)

Данное уравнение - уравнение одного переменного, поэтому его можно решать методом половинного деления, МПИ, методом Ньютона, секущих и т.п.

С помощью найденного определяем .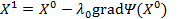

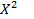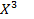, ,..., и т.д. находим аналогично.

Таким образом, выстраивается рекуррентная последовательность

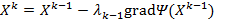,k=1,2,...,

где 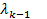-минимальный неотрицательный корень уравнения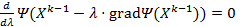

 

Сходимость последовательных приближений к решению уравнения (1) не гарантируется, так как можно попасть в точку относительного минимума.

 

 

Интерполяция.

1. Постановка вопроса (что такое интерполяция?). Пусть заданы значения аргумента и каким-то образом известны (или получены) значения функции f: . Требуется построить функцию F(X), значение которой в фиксированных точках совпало бы с табличными значениями неизвестной функции. Затем построенную функцию F можно использовать для нахождения значений функции f в точках, отличных от фиксированных точек.

Задача, поставленная таким образом, носит неопределенный характер, поскольку через заданные точки можно провести множество функций.

Задача будет носить определенный характер, если мы будем искать не произвольную функцию F(x), а алгебраический многочлен степени не выше n.

Построенный многочлен, числовые значения в фиксированных точках совпадают с табличными значениями функции, носит название интерполяционного многочлена, а фиксированные точки называются узлами интерполяции.

Если точк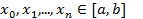и и 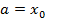, , 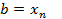а интерполяционный многочлен используется для вычисления f(x) в любой точке 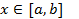, то говорят об интерполировании в узком смысле слова.

Если интерполяционный многочлен используется для вычисления f(x) в точке ,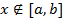

то говорят об экстраполировании в узком смысле слова.

2. Интерполяционный многочлен Лагранжа.

Пусть заданы значения аргумента (узлы) и значения в узлах .

Построим многочлен 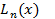степени n такой, что в узлах интерполяции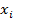

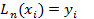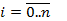, . Предварительно рассмотрим частную задачу: каждому узлу интерполяции поставим в соответствие некий многочлен n-ой степени P_i(x), т.е. 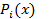ориентирован на узел 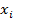так, что

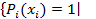
Это означает, что 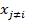(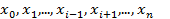) являются корнями многочлена .

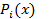Раз 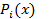- многочлен степени n, то 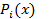имеет вид:

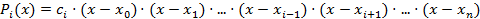
Подберем 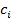таким образом, чтобы 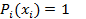. Тогда

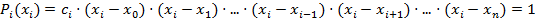
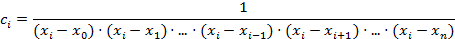
Тогда .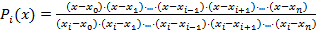

Таким образом, многочлен 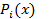определен однозначно. Однако многочлен Лагранжа должен совпадать с определенными значениями в узлах интерполяции. Такой многочлен имеет вид:

+

+ +....+

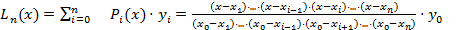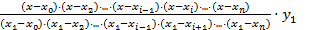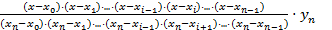
Утверждение. 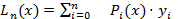- интерполяционный многочлен.

Доказательство. ,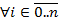

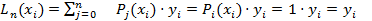что и требовалось доказать.

 

3. Существование и единственность интерполяционного многочлена Лагранжа.

Теорема. Интерполяционный многочлен Лагранжа по заданной системе узлов существует, и притом только один.

Доказательство. 1. Существование доказано в утверждении 1.

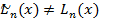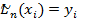
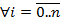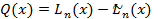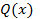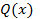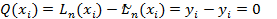2. Докажем единственность. Пусть существует такой, что . Рассмотрим многочлен . является многочленом степени не выше n, так как представляет собой линейную комбинацию многочленов степени n. С другой стороны, у n+1 корень . Действительно, . Но многочлен степени не выше n не может иметь n+1 корень. Следовательно, допущение, что существует многочлен, отличный от исходного, ложно. Таким образом, 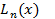является единственным многочленом степени n, проходящим через заданную систему узлов.

Пример. Найти кривую 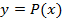, где 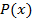- многочлен степени не выше трех через точки (-1,-1); (0,0); (1,1); (2,8)

=

=

= =

 

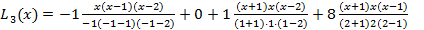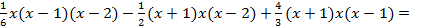
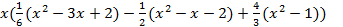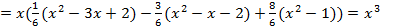
4. Оценка погрешности формулы Лагранжа.

Пусть интерполяционный многочлен 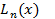совпадает в узлах интерполяции с заданной функцией f(x). В общем случае 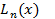в остальных точках отличен от f(x). (исключение-когда функция сама является многочленом степени не выше n. В этом случае 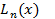= f(x)).

Изучим погрешность метода для класса функций f(x), непрерывных вместе со своими производными до порядка n включительно (т.е. f(x)ÎС_n[a,b] и ).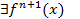

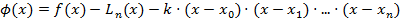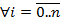
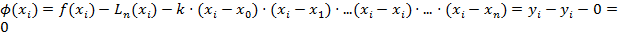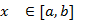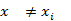
Рассмотрим вспомогательную функцию , где - k некоторая постоянная. Очевидно, что для . Возьмем , 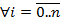и для неё подберем k так, чтобы .

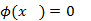Тогда 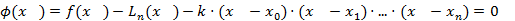, откуда

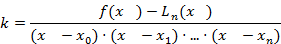
В силу отличия 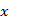от узлов интерполяции знаменатель дроби отличен от нуля

Кроме 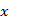, функция 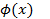обращается в ноль в узлах интерполяции (показано выше). Таким образом, у функции 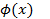имеется n+2 корня.

Замечание.

Теорема Ролля. Пусть 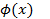- непрерывна и дифференцируема на отрезке [a,b], причем 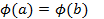. Тогда 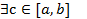такая, что .

 

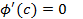Итак, 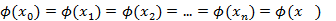. Тогда по теореме Ролля на каждом из отрезков 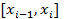, 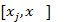и 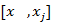имеются точки 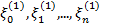такие, что 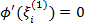. Точно также на каждом из отрезков 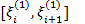найдутся точки 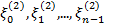такие, что 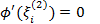. На n+1 шаге найдется точка 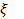такая, что 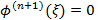. С другой стороны, 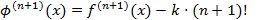и 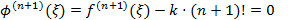, откуда , .

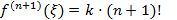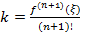Таким образом, 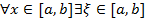такая, что

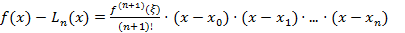(1),

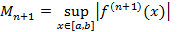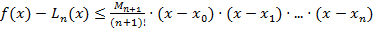или, полагая и (2).

 

Итак, если 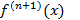может быть оценена, выражения (1) и (2) могут служить оценкой отклонения f(x) от .

 

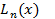5. Другие формы записи интерполяционного многочлена Лагранжа.

=

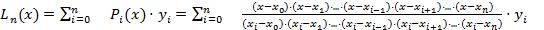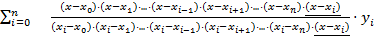
Применим обозначение , = .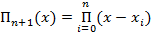

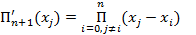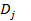Тогда

= .

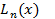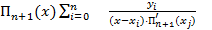Для расчета значения многочлена Лагранжа в точке x èñïîëüçóåòñÿ ñëåäóþùàÿ òàáëèöà:

i	Разности	Di - знаменатель	yi/Di
	x-x0	x0-x1	x0-x2	x0-x3
	x1-x0	x-x1	x1-x2	x1-x3
	x2-x0	x2-x1	x-x2	x2-x3
	x3-x0	x3-x1	x3-x2	x-x3
					Сумма

П(x)- произведение

6. Случай равноотстоящих узлов.

Введем обозначения: 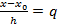, откуда , , , =

= =

= =

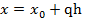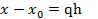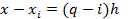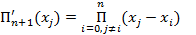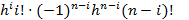
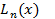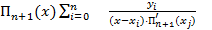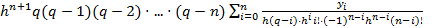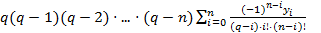
7. Интерполяционный многочлен в форме Ньютона с разделенными разностями.

Рассмотрим случай равноотстоящих узлов с шагом 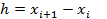=const, i=0,1,2,...,

Определение. Разности между значениями функции в соседних узлах интерполяции называются конечными разностями первого порядка: .

Из конечных разностей первого порядка образуются конечные разности второго порядка:

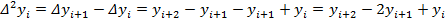
Конечная разность третьего порядка:

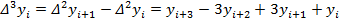
Конечная разность k-ого порядка:

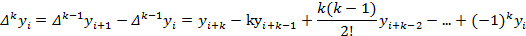
Òàáëèöà êîíå÷íûõ ðàçíîñòåé:

x	y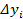

 

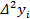
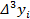
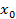
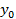
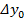
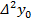
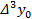
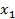
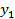
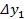
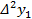
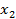
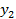
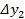
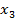
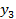
Будем искать интерполяционный многочлен Ньютона в виде:

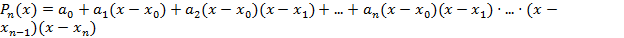degP_n(x)=n.

Подберем значения коэффициентов 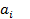из условия совпадения значений исходной функции и многочлена в узлах:

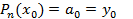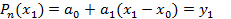, , откуда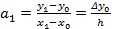

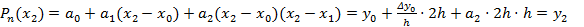, откуда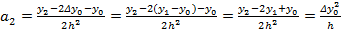

,

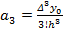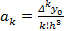
Коэффициенты 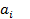называются разделенными разностями k- ого порядка.

Пусть необходимо найти значение в точке x.

Пусть 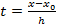, 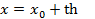. Тогда , ,...,

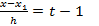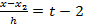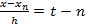
Тогда полином Ньютона

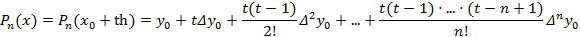
называется первой интерполяционной формулой Ньютона (интерполирование в начале отрезка, t мало по абсолютной величине).

Если значение функции находится в конце отрезка, то используется вторая интерполяционная формула Ньютона:

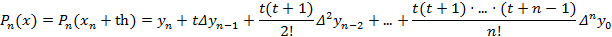
В силу единственности интерполяционные многочлены в форме Ньютона и в форме Лагранжа совпадают.

 

Интерполяция сплайнами

Основная задача интерполяции.

Äàíà òàáëèöà

x	x0	x1	...	xn
f(x)	y0	y1	...	yn

и точка 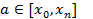, , 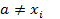i=0..n

Необходимо найти f(a). Нахождение приближенной функции называется интерполяцией (или интерполированием), совпадающей с f(x) в узлах интерполяции.

При большом количестве узлов интерполяции степень интерполяционных многочленов сильно возрастает, что делает их неудобными для вычислений. Этого можно избежать, если на каждом отрезке [x_i, x_i+1] строить самостоятельный интерполяционный многочлен. Однако в этом случае в точках стыка интерполяционных многочленов будет разрывна их частная производная. Поэтому введем особый вид кусочно - полиномиальной интерполяции - интерполяцию сплайнами.

Определение. Сплайн - это функция, которая на каждом частичном отрезке интерполяции является алгебраическим многочленом, а на всем заданном отрезке непрерывна вместе с несколькими своими производными.

Рассмотрим способ построения сплайнов третьей степени (так называемых кубических сплайнов), наиболее распространенных на практике.

Пусть интерполируемая функция f задана своими значениями y_i в узлах интерполяции x_i. Длину частичного отрезка [x_i, x_i+1] обозначим hi= x_i+1-x_i. Будем искать кубический сплайн в ви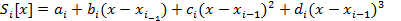де: , где 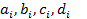-четверка неизвестных коэффициентов. (Всего придется искать 4n коэффициентов).

Потребуем совпадения S_i в узлах с табличными значениями функции f:

,

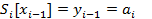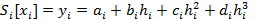
Потребуем также непрерывност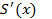и и 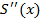в узлах интерполяции. Рассмотри узел x_i:

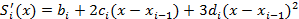
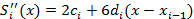
Имеем: 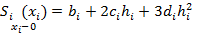, = , 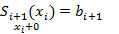i=1,2,...,n-1.(второе уравнение)

Аналогично 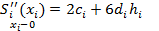, = 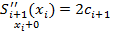. (третье уравнение)

Итак, у нас 2(n-1)+2n условий. Недостает ещё 2 условия (у нас 4n неизвестных).

Если потребовать нулевой кривизны (т.е. равенства нулю второй производной) на концах сплайна, то получим: c₁=0, c_n+3d_nh_n=0. Учитывая, что 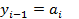,перепишем все уравнения, исключив n неизвестных .

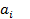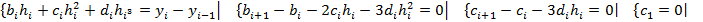
Система состоит из [n+2(n-1)+2]=3n уравнений. Решив её, мы получим значения неизвестных 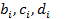, определяющих совокупность всех формул для искомого интерполяционного сплайна.

Рассмотрим использование этого метода на конкретном примере:

Пример 1. Интерполируемая функция задана таблицей, состоящей из четырех узлов (n=3). Требуется найти значения коэффициентов 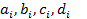, i=1..3, определяющих кубический сплайн на трех частичных отрезках.

i
x
f		-2
hi
		-5

 

Численное интегрирование

1. Постановка задачи

Пусть f(x) - непрерывная функция на отрезке [a, b]. Необходимо вычислить определенный интеграл .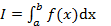

Если существует первообразная F(x) функции f(x), то можно воспользоваться формулой Ньютона-Лейбница .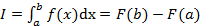

Но могут возникать следующие трудности:

1. Первообразную можно найти, а числовой ответ определенного интеграла - нет.

Невозможно найти первообразную.

3. Функция может быть задана таблицей либо графиком.

В этом случае применяются формулы приближенного (численного) интегрирования.

Основная идея методов численного интегрирования.

Рассмотрим их на графике.

Пусть f(x) - непрерывная функция на отрезке [a, b]. Необходимо найти числовое значение определенного интеграла .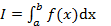

1. Разбиваем отрезок [a, b] на n равных частей, составляем систему узлов 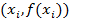и по этой схеме строим интерполяционный многочлен Лагранжа. Принимаем приближенно:

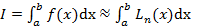. Так получаются квадратурные формулы Ньютона - Котеса.

При n=1 данная формула совпадет с формулой трапеций.

2. Разбиваем отрезок [a, b] на n равных частей и на каждой части строим прямоугольник со стороной f(x_i).

и т.д.

 

2. Методы численного интегрирования.

1. Квадратурные формулы Нютона-Котеса.

Пусть непрерывная функция f(x) определена на отрезке [a, b]. Необходимо найти числовое значение определенного интеграла .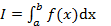

Разбиваем отрезок [a, b] на n равных частей с шагом 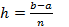. В этом случае можно применить интерполяционную формулу Лагранжа для равноотстоящих узлов: .

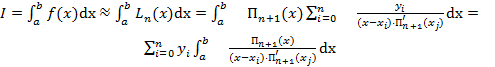Обозначим .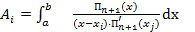

Тогда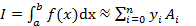

Заметим, что A_i не зависит от f(x), так как они связаны только с узлами интерполяции и если f(x)- полином степени n, то формула становится точной. Так как мы рассматриваем равноотстоящие узлы, A_i можно выразить следующим образом:

= =

=

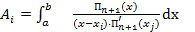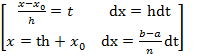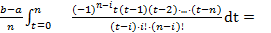
Обозначим 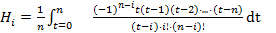. Тогда 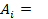(b-a)H_i.

Числа Ai называются коэффициентами Котеса. Они зависят от числа точек разбиения, но не зависят от вида функции f(x). Квадратурная формула Ньютона-Котеса имеет вид:

 

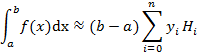
Оценим погрешность формулы Ньютона-Котеса.

Для интерполяционного многочлена Лагранжа имеем:

=

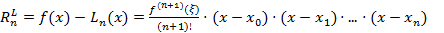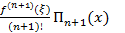
Тогда

/

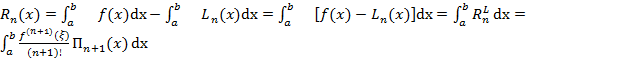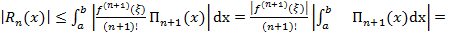
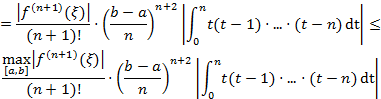
Величина 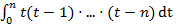является коэффициентом.

 

2. Формула прямоугольников.

Пусть требуется найти 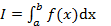. Разбиваем отрезок [a, b] на n равных частей с шагом 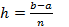. В точках разбиения по оси x выстраиваются перпендикуляры и строится ступенчатая фигура. Для более высокой точности берется большое число разбиений отрезка n.

2.1. Формула малых прямоугольников.

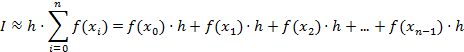
Таким образом, прямоугольники строятся высотой f(x_i) на интервале [x_i, x_i+1].

y

x

x0

x1

x2

xn

2.2. Формула больших прямоугольников.

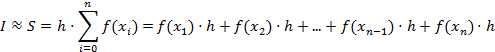
Таким образом, прямоугольники строятся высотой f(x_i+1) на интервале [x_i, x_i+1].

y

x

x0

x1

x2

xn

2.3. Формула средних прямоугольников.

Обозначим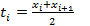

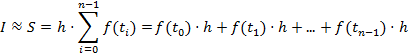
Таким образом, прямоугольники строятся высотой f(t_i) на интервале [x_i, x_i+1].

y

x

x0

x1

x2

xn

t1

t0

tn-1

Ошибки формулы прямоугольников.

1.

 

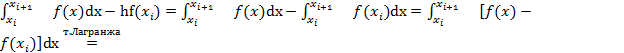
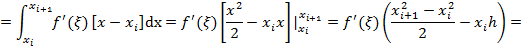
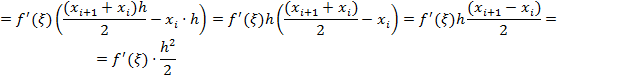
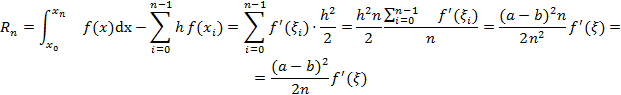
2. Аналогично

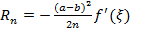
3.

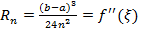
3. Формула трапеции

Пусть требуется вычислить 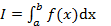. Разбиваем отрезок [a, b] на n равных частей с шагом 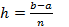. В точках разбиения по оси x выстраиваются перпендикуляры к оси ox до пересечения с кривой f(x). Затем точки пересечения соединяются хордами. таким образом мы вписали n элементарных прямоугольных трапеций в n криволинейных трапеций.

y

x

x0

x1

x2

xn

=

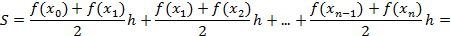
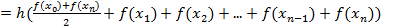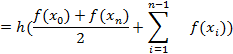
Оценка. Рассмотрим площадь прямоугольного элемента трапеции. Она равна площади подграфика многочлена Лагранжа первой степени на соответствующем интервале [x_i,x_i+1]:

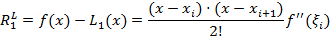
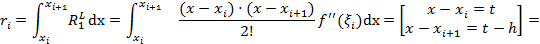
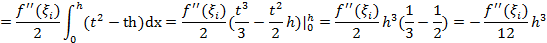
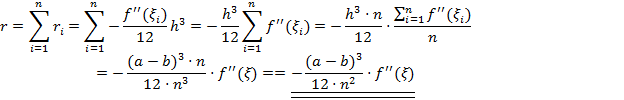
Пусть .

.

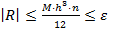Точность не превышает .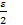

Параболическое интегрирование. Формула Томаса Симпсона.

Пусть задана f(x) - интегрируемая на интервале [a,b] функция. Найти 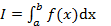. Симпсон предложил разбить отрезок [a,b] на четное число элементарных частей точками x_i, i=0, 1,..., 2n.

Рассмотрим узлы:

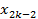
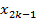
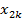
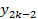
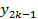
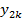
Если эти три точки не лежат на одной прямой, то через них можно провести квадратичную параболу (интерполяционный многочлен второго порядка L₂).

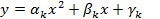; k=1..n.

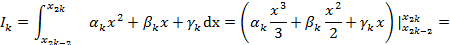
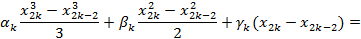
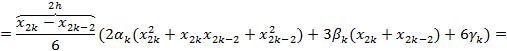
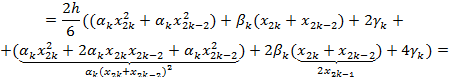
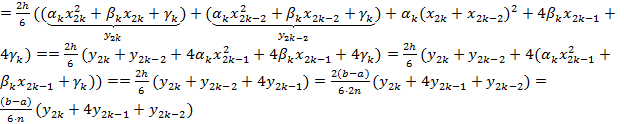Тогда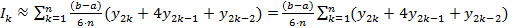

Формула носит имя квадратурной формулы Симпсона.

Оценка погрешности.

,

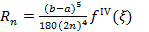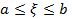
5. квадратурные формулы Гаусса.

Определение. Приближенное равенство 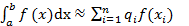, где 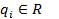- некоторые числа, 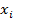-некоторые точки на отрезке [a,b], называются квадратурной формулой, определяемой весами 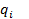и узлами .

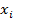Постановка задачи.

Найти среди всех квадратурных формул с n узлами квадратурную формулу с таким расположением узлов 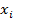на отрезке и с такими весами 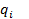, при которых она точна для любых алгебраических многочленов максимальной степени, то есть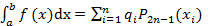

Решение. 1) Заметим, что эта степень меньше 2n, так как при любом выборе узлов 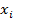и весов 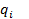многочлен 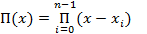степени 2n обладает тем свойством, чт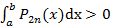о , но .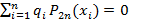

2) Рассмотрим вместо отрезка [a,b] отрезок [-1;1], j=1,2,...,n, 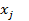- любые несовпадающие узлы.

3) в качестве весов 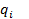возьмем 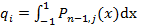, j=1... n, где 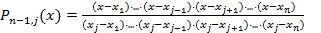-лагранжевы коэффициенты для интерполяционного многочлена степени n-1.

4) покажем точность квадратурной формулы для алгебраического многочлена .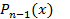

В силу .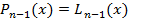

Тогда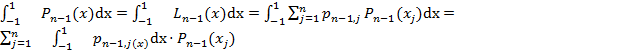

5) Пусть -произвольный алгебраический многочлен степени 2n-1. Представим его в виде

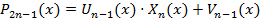, где и 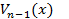-многочлены n-1 степени и частного от деления 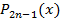на многочлен Лежандра .

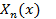Замечание. О многочлене Лежандра.

Определение. Многочлены, задаваемые выражением 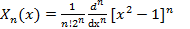называются многочленами Лежандра. Они оргтогональны в смысле скалярного произведения на стандартном отрезке [-1;1], т.е. .

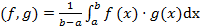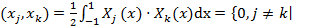. Следовательно, x_n ортогонален любому U_n-1, так как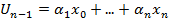

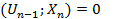
Очевидно, что 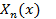- алгебраический многочлен степени n (при n-кратном дифференцировании степень понижается на n) и справедлива лемма.

Лемма. Все корни многочлена Лежандра действительные, простые и расположены в интервале (-1;1).

6) Проинтегрируем равенство (**)

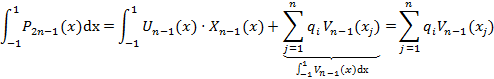
7) В качестве узлов x_j выберем корни многочлена Лежандра x_n. Тогда

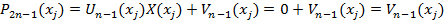
Таким образом,

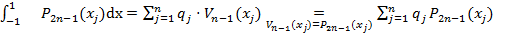
Что и требовалось доказать.

Теорема. Узлы 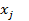, являющиеся корнями многочлена Лежандра, расположены симметрично относительно x=0, а веса 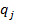положительны и в симметричных узлах совпадают при любом n.

Вывод: для любого алгебраического многочлена 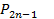существует точная квадратурная формула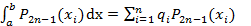

На практике при вычислении метода Гаусса делается замена переменной (если [a,b]¹[- 1,1]): x=(b+a)/2+(b+a)/2*t и

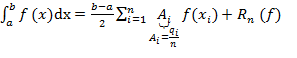, где 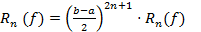- погрешность.

Пример. По формуле Гаусса при n=5 вычислить интеграл .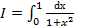

Выполним замену переменной 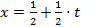. Получим интеграл 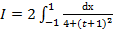. Составим таблицу подынтегральной функции: 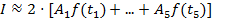=0,78539816

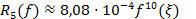, -1<x<1.

 

i	ti	f(ti)	Ai	Ai*f(ti)
	-0,906179846	0,249451069	0,236926885	0,059101665
	-0,53846931	0,237359955	0,47862867	0,113607279
		0,2	0,568888889	0,113777778
	0,53846931	0,157062607	0,47862867	0,075174667
	0,906179846	0,131001136	0,236926885	0,031037691
			Сумма	0,78539816

 

Правило Рунге практической оценки погрешности.

Пусть существует непрерывная 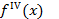-четвертая производная функции f(x) на интервале [a,b]. Пусть 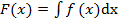. Тогда на интервале 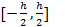исходя из разложения в ряд Тейлора , .

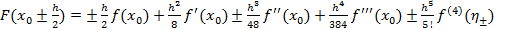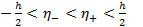Отсюда . Таким образом, .

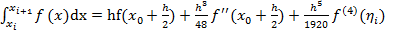Суммируя равенство по i от 0 до N-1 получаем:

.

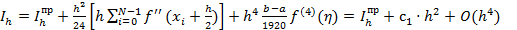Пусть z-неизвестное точное значение некоторой величины, z_h -известное её приближенное значение (решение), зависящее от положительного параметра h. h принимает сколь угодно малые значения.

Предположим, что установлено соотношение 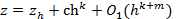(1),

где с- неизвестная не зависящая от h постоянная, k -порядок точности формул