Пусть f(x) - периодическая функция, xÎ(-¥; +¥). Путем линейной замены период можно сделать 2p. В этом случае f(x) можно интерполировать тригонометрическим полиномом.
Введем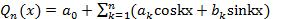 
так, чтобы Qn(xi)=f(xi) 
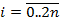, где 
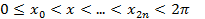-точки промежутка [0,2p).
Полином Qn называется тригонометрическим полиномом порядка n.
Таким образом, необходимо подобрать коэффициенты 
, чтобы выполнялись равенства:
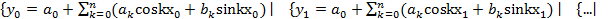
Система линейных уравнений из 2n+1 уравнения с 2n+1 неизвестным. Определитель этой системы отличен от 0.
Следствие.
Теорема 1. Тригонометрический полином Qn(x) порядка n однозначно определяется своими значениями в 2n+1 различных точках, расположенных на промежутке [0, 2p].
По аналогии с интерполяционным многочленом Лагранжа тригонометрический интерполяционный многочлен имеет вид:
(*)
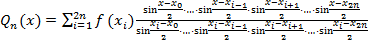Используя формулы
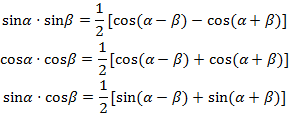
и учитывая, что числитель каждого слагаемого формулы (*) содержит 2n сомножителей, получим, что Qn(x) есть тригонометрический полином порядка n. В силу Qn(xi) = f(xi) это интерполяционный полином. На основании теоремы 1 такой полином единственный.
Вывод. Интерполирование не всегда дает удовлетворительное решение задачи о приближении функции f(x) с заданной точностью на данном промежутке, так как совпадение функции с полиномом Ln(x) (Qn(x)) даже в близких точках xi и xi+1 не гарантирует малость величины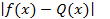 
на отрезке [xi, xi+1]. Более того:
Теорема Фабера. Для любой заданной системы узлов существует такая непрерывная функция f(x), что построение для неё интерполяционный многочлен Лагранжа по этим узлам не сходится равномерно на отрезке [a,b] к f(x).
Пример. f(x)=|x|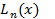 
не сходится равномерно к f(x) ни в одной точке.
Определение. Последовательность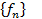 
элементов метрического (нормированного) пространства сходится к его элементу f, если
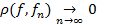- сходимость по метрике;
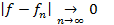- сходимость по норме.
Определение. Если норма задана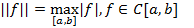 
, то сходимость по такой норме называется равномерной.
Если норма задана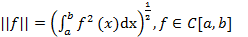 
, то сходимость по такой норме называется среднеквадратической.
Элементы теории равномерного приближения функций
Предмет теории приближения. Теория приближения функций занимается следующими задачами.
1. Рассмотрим множество функций, которое мы обозначим R. Эти функции определены на [a,b]. Рассмотрим подмножество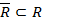 
. Необходимо для заданной функции fÎR с заданной точностью e подобрать функцию jÎ 
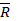такую, что 
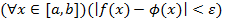. Обычно R 
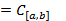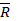, -алгебраический или обобщенный многочлен.
2Для заданной функции fÎR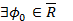 
, для которой имеет место равенство: max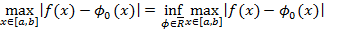 
Если такой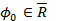 
существует, то её называют функцией наилучшего равномерного приближения к f(x) в классе .
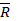Наилучшее приближение в нормированном пространстве.
Пусть R- нормированное пространство. Возьмем в нем n+1 линейно независимых элементов 
и образуем n+1 -мерное линейное нормируемое подпространство 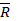всевозможных линейных комбинаций: 
, 
.
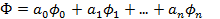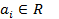При фиксированном f множество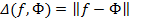 
ограниченно снизу(D- действительные положительные числа, ограниченные снизу). Следовательно, существует точная нижняя грань значений 
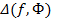. Обозначим её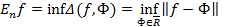 
Число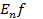 
называется наилучшим приближением функции f с помощью обобщенных многочленов из .
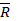Существует ли элемент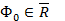 
, для которого 
?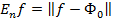